
英语原文共 5 页,剩余内容已隐藏,支付完成后下载完整资料
SOI基槽光波导的色散特性
摘要
狭缝波导的发明使得许多有趣的新型线性或非线性光学应用成为可能,通过引导由高折射率板所保护的纳米宽度的低折射率沟槽中的光。作为其主要特征之一,许多研究已经证明了这种波导的低模态指数。然而,它们的高阶色散特性还没有被彻底研究,而这些器件的尺寸和复杂性以及它们涉及短光脉冲的潜在非线性光学应用需要进一步了解它们的色散行为。我们在这里对围绕1550nm波长的SOI基槽结构的高阶色散特性进行数值研究。结果表明,与传统的通道SOI波导相比,它们可能具有明显不同的二阶色散特性。它们潜在的大的正常色散可能会对各种非线性或线性应用产生影响。还研究了色散性能和波导设计之间的关系,并且结果可以显示更多的的场所来优化或控制这种波导的色散特性。
1.引言
狭缝波导结构自2004年首次提出以来,由于其在低折射率狭缝区域中具有高电场分布的光限制能力而引起了重大研究兴趣。基于介电材料的各种无源和有源结构,特别是绝缘体上硅(SOI)以及其他材料已经在理论上被研究或实验制造。随着制造工艺越来越成熟,已经制造出具有越来越复杂设计的各种功能器件,例如环形谐振器,调制器,干涉仪以及用于潜在光通信或感测应用的槽结构。由于纳米尺度狭缝区域内的场强可能非常高,因此狭缝波导也可能成为高非线性集成光学器件的良好候选。对改善非线性性能的模态场分布的设计和优化也有很大的兴趣。
狭缝波导的一个有趣和重要的性质是其传播模式的低有效指数,其明显低于传统波导的有效指数。这是由于在低折射率缝隙区域受到光的限制。对于基本缝隙波导结构以及一阶色散关系,模式有效折射率在过去已经得到了理论和实验研究。然而,由于这些波导器件增长到更大的复杂性和尺寸,并且可以在宽带光输入下工作,例如用于非线性全光学应用的超短光脉冲泵,所以这些波导中的高阶色散效应类似于其光纤对中的那些,除了非线性特性外,还可能成为一个需要考虑的重要因素。然而,到目前为止,还没有系统地研究更高阶的色散特性(例如群速度色散(GVD))以及它们与时隙波导的设计或参数的关系。
在本文中,我们通过数值研究了光纤通信波长周围的缝隙波导结构的色散特性,并系统地研究了它们与波导结构的一些关键参数的关系。我们的研究结果表明,与传统波导相比,时隙波导具有不同且独特的色散特性,并且可能对其一些潜在应用产生影响。
理论分析
我们在这里研究了最广泛研究的槽结构,如图1所示。两个高折射率的矩形平板被埋在低折射率包层材料内。 板之间的槽区用低折射率材料填充,该折射率材料可以是与包层材料相同或不同的材料。板或槽的高度为h,槽的宽度为ws,每个板的宽度为wb。
在这项研究中,考虑了基于SOI的波导,其中包层和衬底包含熔融石英,并且板由硅制成。它们可以通过沉积额外的SiO2层来覆盖SOI晶片上的纳米硅特征。当狭缝未在沉积过程中填充SiO2时,该狭缝被认为是填充有熔融石英或被空气占据。
全矢量有限元算法用于计算波导的模态特性。由于对称准TE模式是上述缝隙波导结构中缝隙中具有高功率限制因子的指导基模,研究了准TE模式的模态特性。其模态有效折射率n可以通过分析模态传播常数找到。
在此,为了研究群速度色散,我们使用色散参数D来表示波导的二阶色散效应,其被定义为群延迟相对于波长的导数,并且可以基于模态有效指数n由
vg是群速度。
在这项工作中,硅(Si)和二氧化硅(SiO2)是所用的介电材料。对于熔融石英,其折射率nSiO2可用Sellmeier方程描述
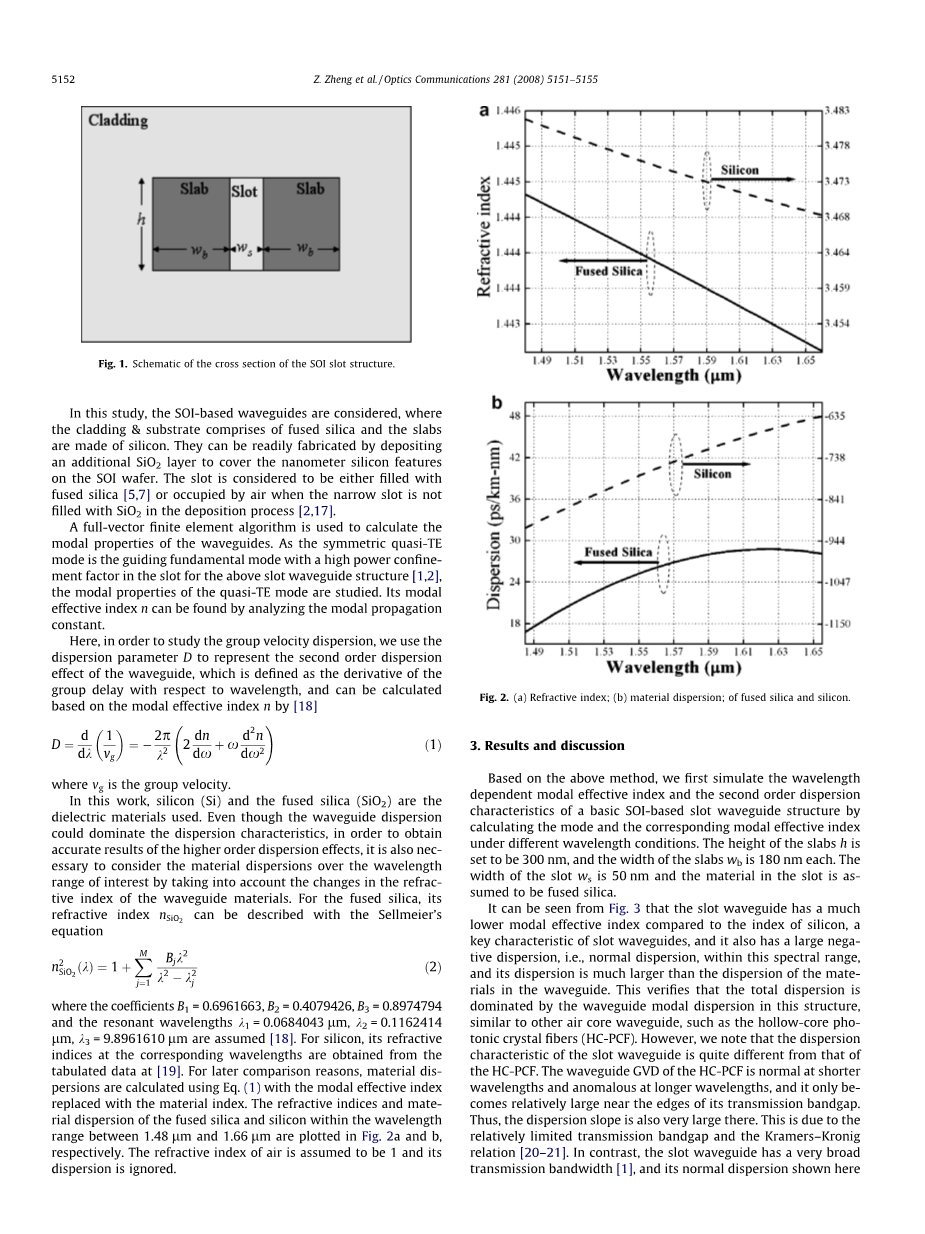
假设系数B1 = 0.6961663,B2 = 0.4079426,B3 = 0.8974794并且谐振波长k1 = 0.0684043 um,k 2 = 0.1162414 um,k3 = 9.8961610 um。对于硅,其相应波长处的折射率可从表中的数据获得。为了以后比较的原因,材料分散使用公式(1)将模态有效指标替换为材料指标。图2a和b分别绘出了熔融石英和硅在1.48 um和1.66 um之间波长范围内的折射率和材料色散。空气的折射率被假定为1并且其分散被忽略。
结果与讨论
基于上述方法,首先通过计算不同波长条件下的模式和对应的模态有效指数,模拟基本的基于SOI的时隙波导结构的波长依赖模式有效指数和二阶色散特性。板坯h的高度设定为300nm,板坯wb的宽度分别为180nm。槽的宽度W s为50nm,并且槽中的材料被假定为熔融石英。
从图3中可以看出,缝隙波导相比作为缝隙波导的关键特性的硅的折射率具有低得多的模式有效折射率,并且还具有大的负色散,不同于正常色散。在此频谱范围内,其色散远大于波导中材料的色散。这验证了这种结构中的总色散主要受波导模式色散的影响,类似于其他空心波导,例如空芯光子晶体光纤(HC-PCF)。但是,我们注意到时隙波导的色散特性与HC-PCF的色散特性完全不同。HC-PCF的波导GVD在较短的波长处是正常的,在较长的波长处是异常的,并且在其传输带隙的边缘附近其仅变得相对较大。因此,在那里色散斜率也非常大。这是由于传输带隙和Kramers-Kronig关系相对有限。相比之下,缝隙波导具有非常宽的传输带宽,并且其在这里示出的正常色散在宽光谱范围内可以更大。对于亚皮秒光脉冲,对于这种缝隙波导,色散长度将仅为几毫米甚至更短。因此,对于可用于使用短光脉冲作为泵浦源的非线性应用的许多缝隙波导器件而言,尽管器件看起来很短,但色散效应可能是不可忽略的因素。
为了比较,具有的410nm的宽度和300nm的高度基于SOI的通道波导的分散性也计算。假定该通道波导由与槽波导相同的材料制成,并具有相同的高度和宽度,其等于上述平板和槽的宽度之和。 因此,信道波导对应于ws = 0的上述槽波导,并且wb = 205nm。分析了信道波导的准TE模式,如图3所示,其色散特性明显不同。
信道波导的色散参数处于正区域,而槽阵结构则处于负区域。信道波导的色散绝对值比时隙波导的绝对值小得多。因此,我们看到,槽波导结构与具有非常相似几何形状的传统波导相比具有非常不同的高阶色散特性,这可能归因于独特的槽结构。上述结果还可以打开使用槽波导结构的有趣应用 用于传统SOI波导的色散补偿应用。
基于上述观察,我们进一步研究了缝隙波导的色散特性对一些结构值的依赖性。
首先,考虑槽宽w s对GVD的影响,其中板的尺寸保持相同,但两个板之间的间隔是变化的。槽中的填充材料仍然被认为是熔融石英。如图4所示,当ws增加时,模态索引减小,因为较低索引时隙区域中包含更多字段。另一方面,GVD结果也发生显着变化。在这种情况下,短波长色散值的大小随着ws的增加而显着增加。而且,D曲线的斜率现在也不同,例如三阶色散。随着ws从50 nm增加到110 nm,斜率从大部分负值变为正值。值得注意的是,在特定的ws值处,色散参数可以在特定波长附近保持几乎恒定。例如,当ws = 70nm时,色散曲线在1580nm和1650nm波长之间几乎是平坦的。因此可以实现具有最小色散斜率(例如三阶色散)的隙缝波导结构。
槽中的材料和槽区的宽度都是变化的; 通过模拟槽中空气的情况(如图1所示)和槽中充满熔融石英的情况。
接下来,我们研究不同槽材料对GVD的影响。在这里,我们用充满空气的槽代替熔融石英来计算模式特性。由于空气具有比熔融石英低的折射率,所以在相同的波导几何形状下,模式有效折射率也较低。与熔融石英填充波导相比,充气隙缝波导具有更大的负GVD。当ws变化时,短波长处的色散值的幅度随着ws增加而稍微增加。然而,在特定的波长,例如1480nm处,这种变化在某些ws值下可能不明显,这可能表明色散特性不易受到槽宽变化或制造误差的影响。与图4,在这些ws值下,色散斜率都是正的,而随着ws的增加,斜率也变得越来越正,类似于图4的情况。因此,可以看出,波导材料的选择也具有显着的效果关于波导的色散特性(见图5)。
最后,对包含空气或SiO2 -槽结构的上述两种波导结构研究了板宽wb对色散值的影响。槽宽保持在50nm。结果如图6和7所示。随着板坯宽度的增加,模态有效指数增加,这是因为板块中有较大部分的场地。然而,这两种情况下色散曲线的变化可能会有很大的不同。对于SiO2-波导波导,色散值的大小减小,色散斜率逐渐增大。对于空气隙波导,色散值的大小增加,色散斜率的变化较小。
结论
这里已经给出了基于SOI的槽式光波导的二阶和更高阶色散特性的数值分析。通过比较传统波导结构和槽结构的色散,发现埋入SOI隙缝波导结构的色散曲线处于1550nm光纤通信波长附近的正常色散区域,而对于可比较的常规结构,其分散处于异常分散状态。狭缝波导也可以具有比传统的通道波导大得多的GVD,并且当其应用于涉及超短光脉冲的应用(例如四波混频,参数相互作用和脉冲压缩)时,色散可以发挥重要作用。
我们的结果表明,这些槽波导的高阶色散行为(包括色散斜率)高度依赖于波导的几何参数,例如槽和平板宽度,以及形成这些波导结构的材料。根据这里给出的结果可以考虑各种色散优化或补偿应用。应该指出的是,我们对非常基本的缝隙波导结构的结果表明,当波导结构改变时,缝隙波导的色散特性可以显着变化,因此,考虑到大量不同类型的缝隙波导设计,对此进一步研究 主题可能是必要的。
致谢
北京航空航天大学的工作得到了国家自然科学基金资助60407010,863高科技计划(2006AA03Z310),NCET计划和PCSIRT计划,SEM的支持。
具有四个零色散波长的硅波导及其在片上倍频跨越超连续谱产生中的应用
摘要:据我们所知,我们首次提出了一种新型硅波导,它首次展现出四个零色散波长,在670nm带宽上具有平坦的色散。这对探索新的非线性效应和在硅芯片上实现超宽带信号处理具有巨大的潜力。作为一个例子,我们表明,在1217到2451nm的波长范围内,几乎从带隙波长到半带隙波长,可以在硅中获得由色散波产生辅助的倍频跨越超连续谱。输入脉冲被大大压缩到10 fs。
引言
色散是光波导的基本特性之一。它不仅形成沿波导传播的光脉冲的时间波形,而且还与非线性一起影响脉冲光谱展宽。特别是,零色散波长(ZDW)在确定非线性参数过程中的相位匹配条件和转换效率方面起着至关重要的作用。二氧化硅阶跃折射率光纤通常在近红外波长处表现出一个ZDW,而光子晶体光纤(PCFs)提供了调整色散特性的良好机会,能够产生三个或四个ZDWs并大大调整它们的光谱位置。色散的这种光谱特性强烈地影响光纤中的非线性过程(例如,超连续光谱的产生),并产生丰富且前所未有的现象。
具有高非线性的集成波导最近引起了很多兴奋。特别是,在飞秒脉冲或倍频程跨越频谱展宽的情况下,在宽波长范围内的平坦和低色散变得可取。两个ZDW在高折射率对比波导中的色散调整被提出。最近,提出了分散平坦化技术,产生了20倍的分散平坦度和三个ZDW。色散剪裁有助于在集成的硫族化合物和氮化硅波导中进行倍频跨越的超连续谱生成,其中折射率对比度低于硅波导,并且波导色散变小。然而,这种超连续谱生成需要高输入峰值功率飞秒脉冲,这仅在双光子吸收(TPA)不存在或极低的材料平台中才是可行的。在硅波导中,强分散和相当大的TPA使得实现倍频程超连续性相当具有挑战性。
据我们所知,我们首次提出了一种硅狭缝波导,其波长范围从1461nm到2074nm,具有四个ZDW。色散值和ZDW位置可以变化,这为探索诸如孤子传播,调制不稳定性,超连续谱和频率梳产生等丰富的非线性效应提供了很好的机会。 我们通过模拟显示,独特的色散有助于在硅芯片上从1217到2451 nm产生倍频跨越超连续谱。在这个过程中,输入脉冲被大大压缩到10 fs。
具有四个ZDW的色散平坦硅槽波导
波导具有在两个硅层之间形成的水平二氧化硅槽,如图2所示。1.波导参数为:宽度W = 610nm,上部高度H u = 136nm,下部高度H l = 344nm,以及狭缝高度H s = 40nm。 埋入的氧化物衬底厚度为2mu;m。为了计算准TM模式(垂直偏振)的色散,我们使用全矢量模式求解器COMSOL,考虑了Si和SiO2的材料色散,得到了作为波长函数的有效折射率。
图2显示了硅材料的色散和准TM模式的平坦分散,计算公式为。在667nm带宽上,色散从1435到2102nm在-22和 20ps /(nm·km)之间变化。如图2(b)所示,分别在1461,1618,1889和2074nm处发现四个ZDW。定义为的群延迟从1403到2146nm具有40fs / cm的小变化,这产生超宽带群速度匹配 用于飞秒脉冲相互作用。
生成四个ZDW的想法如下。首先,硅中的材料色散在感兴趣的波长处总是负的(参见图2(a))。形成波导时,我们看到,在接近Si带隙波长(〜1100 nm)的短波长处,材料色散占主导地位,因此总体色散为负值。在导波模式接近截止的长波长处,色散主要由波导色散占主导。因此,只要定制波导尺寸,使得在中波长范围内,波导色散是正的且比材料色散更强,则可以用两个ZDW获得正整体色散[18]。然后,我们使用由模式转换引起的反交叉效应,也就是说,随着波长的增加,导模从更多的带状模式演变为更多的缝隙模式(见图1)。这导致额外的负波导色散[20],并在中间产生另外两个ZDW。
可以根据上面给出的值改变波导中的结构参数,以调整色散值和斜率我们单独减少上部高度并增加下部高度,同时保持其他高度。色散曲线从图3中的正常色散移动到反常色散区域,色散值分别变化为每nm 18.5和15.9 ps /(nm·km)。 没有观察到色散斜率的显着变化。
如图4(a)所示,色散斜率可以通过改变狭缝高度从32nm到48nm而大大地调整。另一方面,随着波导宽度的增加,ZDW在ZDW之间以间距改变移动,这导致色散轮廓的轻微旋转。尽管高折射率对比波导中的色散特性可能对制造缺陷敏感,但通过改变结构参数的色散可定制性给了我们设备设计的宝贵空间。<!--
全文共7925字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[14272],资料为PDF文档或Word文档,PDF文档可免费转换为Word


