利用表面等离子体波测金属薄膜的厚度和光学外文翻译资料

 2022-04-12 08:04

英语原文共 9 页，剩余内容已隐藏，支付完成后下载完整资料

利用表面等离子体波测金属薄膜的厚度和光学

常数

W．P．Chen J．M．Chen

摘要：讨论了在没有预设介电常数ε(omega;)的表达式的情况下，用于确定金属膜介电常数ε(omega;)和厚度d的表面等离子体波方法。在给定频率下可以得到两组解。通过比较在另一频率下确定的厚度d，介电常数ε(omega;)和膜厚d就被确定下来。

正文：金属膜的光学性质可以用与频率相关的介电常数ε(omega;)来表征。在众多光学方法中，表面等离子体波方法(SPW)特别适用于研究几十纳米厚金属薄膜的介电常数ε(omega;)。最近，Lopez-Rios和Vuye利用表面等离子体波方法测得了银薄膜的介电常数ε(omega;)和厚度d，他们在4000-6000Aring;范围的SPW共振激励下，进行了反射率的最小二乘拟合。对于银的介电常数，他们采用了频率相关函数，该函数考虑了电子的带内跃迁和从3.86eV开始的带间跃迁的贡献。只要介电常数ε(omega;)的表达式是已知的，这种方法很好的确定了膜厚d以及在ε(omega;)表达式中用的参数。然而，在许多研究中，包含来自带间转换贡献的ε(omega;)的预设表达式是不知道的。因此，在没有给定对应频率ε(omega;)的预设表达式的情况下，我们需要一种能够测得介电常数ε(omega;)和厚度d的方法。首先提出这种方法的人是E. Kretschmann，并且这种方法后来被人引用。已经确定可以从给定频率的SPW的反射最小值中找到唯一的一组介电常数ε(omega;)和膜的厚度d的解。

在本文中，我们即将讨论没有预设介电常数ε(omega;)值的情况下，利用表面等离子体波方法测得金属薄膜介电常数和厚度。我们发现两组ε(omega;)和d的解可以从给定频率的SPW谐振激励得到，一个对应于阻尼SPW的欠偶合，另一个对应于阻尼较小的SPW过耦合。再用另一个频率下的解，就可以得到唯一的真解，即对应于两个频率具有相同的d解。为了便于讨论，我们将简要地回顾Kretschmann损耗全反射(ATR)配置中SPW的激发。考虑如图1所示的棱镜-金属-真空的结构，当一束频率为omega;的P偏振光以角度theta;入射，并且theta;大于临界角theta;c时，它可以直接与金属-真空中的表面等离子体波耦合（theta;c=sin-1(1/n)，其中n是棱镜的折射率）

。当入射光的频率和Kx(theta;)与表面等离子体波的频率以及复波矢相匹配时，就会产生共振效应（Kx(theta;)是入射光矢量在平行于界面方向的投影）。由于Kx是实数，而K是复数，所以只能在Kx(theta;)=Re(K)时达到近似匹配。

theta;=theta;ATR= sin-l[Re(K) c/n] （1）

在角度为theta;ATR时，会发生入射光的全反射损耗。耦合可以通过计算光源的反射率R来分析。

图1 Kretschmann模型

根据菲涅尔公式，三层结构的光反射率可以表示为

（2）

式中：

（3）

（4）

Kjz=(εj-Kx2)1/2 (j=1,2,3) （5）

Kx=n （6）

式中，下标1，2，3分别表示金属，空气和棱镜。εj是各材料的介电常数；Kzj为在媒介j中垂直于分界面的波矢分量；d为金属薄膜的厚度；Kx为激发表面等离子体振荡的光波在x轴方向的波矢分量；并且lambda;=2pi;c/omega;为真空中的光波长。各层介质的介电常数分别为ε1=εr iεi，ε2=1和ε3=。

当入射角接近于theta;ATR时，反射率R可以表示为theta;的函数，即

（7）

式中K=K0 KR，。并且K0和KR可以通过下面两式给出：

（8）

（9）

这里K是Kretschmann结构中SPW的复波矢， K0是没有棱镜耦合时金属—真空界面上SPW的复波矢，KR为棱镜耦合时K0的扰动项。K0和KR的虚部分别是本征和辐射损耗。前者表示金属中的焦耳损耗，后者表示SPW泄漏到棱镜中的泄漏损耗。反射率在theta;ATR处具有洛伦兹倾角，具有半宽度Wtheta;和最小反射率Rmin。半宽度和最小反射率可以通过以下公式给出：

（10）

（11）

eta; =Im（K0）/Im(KR) （12）

根据等式（1）-（12），我们可以从测得R与theta;的关系曲线来测得金属薄膜的介电常数ε1和厚度d。通过差分校正和迭代的方法来拟合公式（2），即可仿真求出最佳拟合的金膜介电常数和金属膜厚度d。具体的拟合求解过程如下：

（1）将由SPR实验曲线获得的共振角theta;ATR代入公式（1）中，求出Re（K）；

（2）因为Re（KR）lt;lt;Re（K0），所以可令Re（K0）=Re（K）；

（3）通过公式（8）的实部，确定金属薄膜介电常数的实部εr；

（4）将实验获得的共振角theta;ATR和半宽度Wtheta;代入公式（10），用于确定Im(K0) Im(KR)=Im(K)；

（5）将实验获得的反射率最小值Rmin代入公式（11），用于确定Im(K0)/Im(KR)；

（6）通过步骤（4）和（5），可以分别确定Im(K0)和Im（KR）；

（7）将εr和Im(K0)代入公式（8）的虚部，可以确定金属膜介电常数虚部εi；

（8）将theta;ATR、εr、εi和Im（KR）代入公式（9）的虚部，可以确定金属膜厚d。

按照上述步骤，将实验获得的反射率最小值Rmin代入公式（11）中，会得到两组Im(K0)/Im(KR)解，因此会得到满足以上求解步骤的两组ε1和d的初值。这两组解互为倒数，其中一组解对应于本征损耗大于辐射损耗（即欠耦合情况），另一组解与之相反（即过耦合情况）。欠偶合情况时估算的膜厚度d大于过耦合情况时的d取值。在没有棱镜的情况下，对应于欠偶合情况下的SPW传播长度比对应于过耦合的SPW传播长度短。然而，对于一阶近似，这些表面等离子体波在一些ATR结构中很难区分。作为初值的这两组解均能满足迭代过程，并且得到非常好的拟合曲线，很难从中确定真解。因此，当入射光波频率一定时，通过角度调制SPR反射率曲线，按照上述步骤可以仿真求出两组ε1和d解。利用金属膜厚度d与入射光频率无关的性质，通过比较两组波长下的ε1和d的解，可以从中确定ε1和d真解。

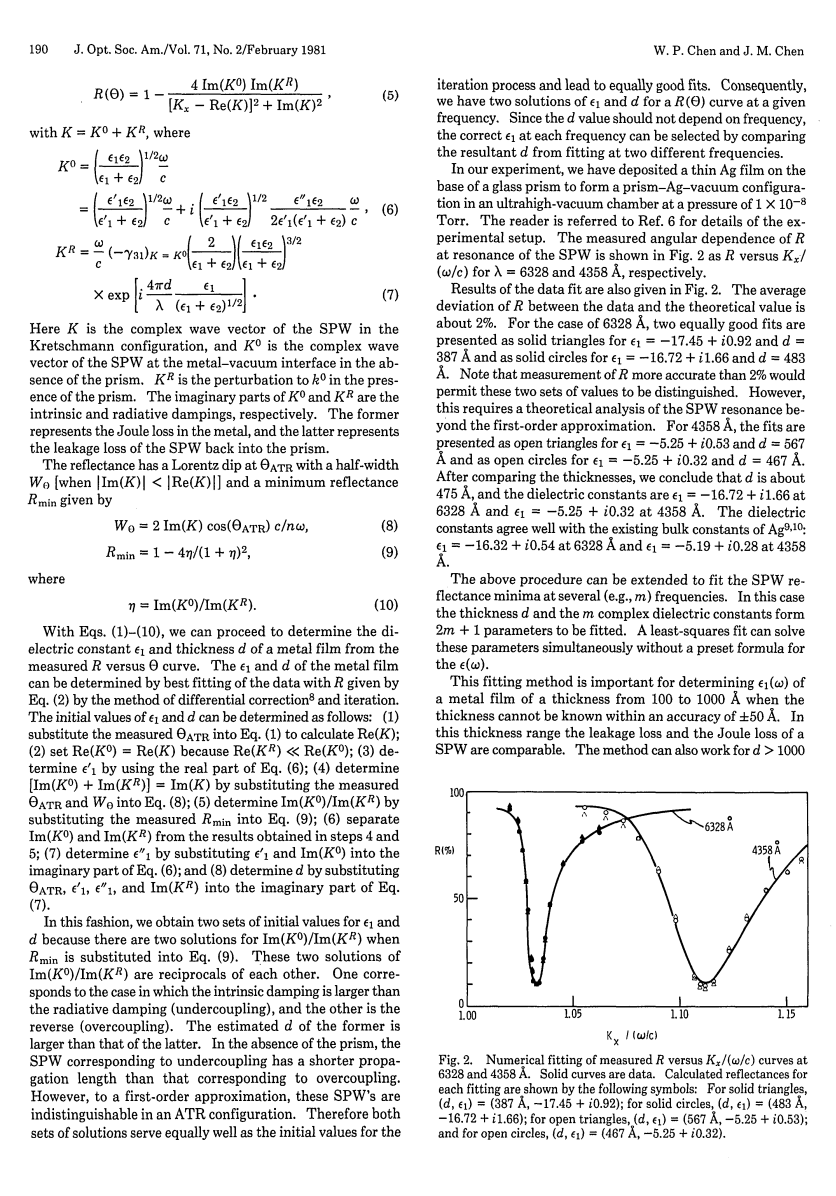
在我们的实验中，我们已经在玻璃棱镜上沉积了一层薄薄的银膜，在110-8乇的压力下的超高真空室中形成棱镜—银—真空结构。读者可以参考参考文献6了解实验装置的详细信息。在SPW发生共振时，测得的角度依赖于反射率R，如图2所示的R与Kx/（omega;/c）在波长分别为632.nm和435.8nm时的关系。

图2 R与Kx/（omega;/c）在波长为632.nm和435.8nm的关系图

数据拟合的结果也在图2中给出。R的实验结果与理论值的平均偏差约为2%。对于波长为632.8nm的情形，有两个很好的拟合解，其中一组解用实心三角形标示出，ε1=-17.45 0.92i，d=38.7nm；另一组解用实心圆标示出，ε1=-16.72 1.66i，d=48.3nm。注意到此时测得的反射率R的值比理论值要精确2%，所以这两组解能够区分。然而，这需要对超出一阶近似的SPW共振进行理论分析。对波长为435.8nm而言，两组拟合解表示为ε1=-5.25 0.53i，d=56.7nm（三角形标识）和ε1=-5.25 0.32i，d=46.7nm（圆形标识）。在比较厚度之后，得出结论：膜的厚度d约为47.5nm，介电常数在632.8nm为ε1=-16.72 1.66i，在43.58nm为ε1=-5.25 0.32i。介电常数与现有银在对应波长的介电常数相一致。

上述过程同样可以适用于测得m频率下的SPW反射率的最小值。在这种情况下，厚度d和m个复数介电常数形成2m 1个拟合参数。最小二乘拟合可以同时解决这些参数，而不需要预先了解介电常数ε(omega;)的表达式。

这种拟合方法对于确定厚度从10到100nm的金属薄膜的ε(omega;)是非常关键的，但是当厚度在0.5nm以内时，精确度是不可知的。因为在这个厚度范围内，SPW的泄漏损耗和焦耳损耗是可比拟的。这种方法同样适用于膜的厚度d大于100nm的情况，但是由于泄漏损耗远小于焦耳损耗，因此ε1可以通过取K=K0（忽略KR），由式（1）、（8）和（10）简单的确定。由近似方法得出的ε1与由精确拟合得出的ε1的偏差仅有（1-Rmin）/ 4。例如，当Rmin=90%时，偏差仅为2.5%。最小二乘拟合也可以用于在dlt;10nm时R(theta;)曲线的拟合。对于这种情况，因为角度依赖于金属膜中的电磁场，而该电磁场主要由ε1和ε2决定，反射率R（吸收为1-R）显示对角度的依赖性而不显示对ε1的依赖。反射率的绝对值取决于d和εi的乘积（该乘积等于吸收系数和电子面积密度的乘积），最小二乘拟合只给出d和εi的乘积，而不是精确的给出εr或者εr与d的乘积，d和εi之间的相关性不能通过在不同频率下的更多数据来消除，但是可以通过其他方法测定的d值来消除。

总之，在给定频率下，同时满足SPW共振条件，我们可以得到两组解ε1和d。一组解对应于阻尼SPW的欠偶合，另一组解对应于小阻尼SPW的过耦合。在另一个频率确定的厚度d的帮助下，我们可以区分这两组解。因此，再没有预设ε(omega;)的表达式的情况下，金属薄膜的厚度和光学常数可以通过在任意给定频率下的表面等离子体波的共振来确定。

超薄金属薄膜的SPR相位检测研究

刘超，刘庆刚，李婷婷

摘要：本文采用SPR相位检测方法测量纳米级金属薄膜厚度，它提供了一种新颖的方法计算厚度值，通过计算干涉条纹相对于从薄膜基底台阶覆盖的棱镜反射的TM偏振和TE偏振波的相对偏移。仿真结果表明了相位变化与金属膜厚度之间的关系，该方法成功的测量了标称厚度为50nm的目标金属薄膜，平均测量值为50.02nm。标准偏差为0.41nm，最大重复性误差为0.90nm。

关键词：SPR效应；相位检测；金属薄膜厚度；纳米；干扰

简介：薄膜方法在过去的一些年中已经广泛的应用于微电子，光电子，航空航天，生物工程，医疗器械和高分子材料等领域，特别是纳米级金属薄膜的研究由于其独特的的性质而成为热点，而这些性质取决于许多方面，比如反射率，折射率和膜厚度。金属膜厚度参数对光学，力学和电磁性能起着决定性的作用，因此如何准确测量金属膜的纳米级厚度已成为关键方法。

目前，薄膜的主要测量方法包括干涉仪，椭偏仪，高精度显微镜测量和探头测量。干涉测量法是一种简单光路的非接触式方法，但通常只适用于折射率已知且厚度均匀的透明或半透明薄膜。椭圆偏振测量法利用反射或透射光的偏振状态与入射椭圆偏振光相比测量薄膜厚度的变化，而它仅适用于测量厚度小于一个周期的透明或弱吸收薄膜。高精度显微镜测量使用扫描隧道显微镜或原子力显微镜检测金属膜厚度，探针测量使用触针表面轮廓测量系统来测量金属膜厚度。由于样品的膜基底步骤，上述两个测量将会导致薄膜样品的完整性受到不同程度的损害和破坏。SPR效应的应用主要涉及生化测量和光纤传感器领域，清华大学俞兴龙教授的研究小组一直致力于SPR生物传感器的研究。在利用棱镜反射光方法测量溶液浓度的实验中，发现棱镜斜边的金属膜厚度对入射光的反射率和反射相有直接的影响。因此，本团队致力于研究基于SPR效应的纳米金属薄膜厚度相位检测方法，以克服上述方法的缺陷。

  1. 表面等离子体共振（SPR）的

    全文共8091字，剩余内容已隐藏，支付完成后下载完整资料

    资料编号：[14149]，资料为PDF文档或Word文档，PDF文档可免费转换为Word

原文和译文剩余内容已隐藏，您需要先支付 30元 才能查看原文和译文全部内容！立即支付

以上是毕业论文外文翻译，课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。

您可能感兴趣的文章