英语原文共 6 页,剩余内容已隐藏,支付完成后下载完整资料
基于滑动求和的高效准确的高斯图像滤波
摘要:本文提出了一种利用高斯核卷积图相关的简单而有效的方法。通过利用图像行和列的滑动求和的方式对每个像素进行恒定数量的计算。我们研究了用于内核近似的误差函数及其与输入信号特性的的关系。基于自然图像统计,我们提出了一个二次型内核误差函数,使输出图像的二级误差最小化。通过常数函数的线性组合逼近高斯内核。这是非常高效的高斯滤波方法。我们的实验表明所提出的技术比最先进的方法更快,同时还能保持一个类似的精度。
索引关键词:非均匀滤波,高斯核,积分图像,自然图像统计。
一 引言
图像滤波是一种无处不在的图像处理工具,它需要快速、高效的计算。当内核的大小增加,内核响应的直接计算需要更多的操作,过程因此变得缓慢。有关特定内核在线性时间内的快速卷积的各种方法已被提出(见相关工作在第二节)。高斯内核是一个在许多应用中都被使用的重要的内核。
在本文中,我们提出了一种用于可分离的、非均匀核的高效滤波算法并把它应用于快速准确的高斯滤波中。我们的方法是沿着图像单行单列进行一维的滑动求和(积分图像)。提出的算法是非常简单的,可以写成几行代码。复杂性分析以及实验结果表明保持类似的逼近精度时它比最先进的用于高斯卷积的算法更快。
本文的另一个贡献是内核的近似和与滤波后的最终输出的近似结果之间的关系分析。通常,逼近的质量是通过内核和它的近似值之间的差异来衡量的。然而,最大限度地减少内核错误不一定能减少对最终图像的误差。为了尽量减少误差,应该考虑自然图像统计。
在第四节中,我们调查内核逼近误差函数。基于自然图像统计我们发现一个对输出的像素值二级误差最小化的二次型核误差测量。
下一节综述了快速的非均匀图像滤波的相关方法,第三节介绍了滤波算法并讨论了它的计算方面,第四节讨论内核逼近与自然图像统计的关系,第五节介绍我们的实验结果,我们的结论在第六节。
二 相关工作
接下来我们回顾计算图像滤波的主要方法。我们更详细地描述了基于积分图像以目前工作为基础的方法。
一般多尺度方法。用一个尺寸为k的任意核卷积一个像素为n的图像可以在O(n,k)直接计算操作,或在O(n log K)操作中使用快速傅里叶变换。
一种更有效的方法是线性时间内使用图像金字塔的多尺度计算。粗糙的图像水平被小的内核过滤,结果插补到更精细的水平。用一个大的高斯内核使图像的卷积近似。
递归滤波。递推法是一种非常有效的一维滤波(或分离)的内核的方法。所需内核的无限脉冲响应(IIR)表示为Z空间中的双多项式的比值。然后用差分方程计算给定信号的卷积。递归算法提出了高斯内核中各向异性的高斯分布和Gabor核的近似滤波。
Deriche和年轻凡弗利特的方法是现在的快速近似高斯滤波的最先进的方法。为了考虑前后相邻的内核响应,这两种方法展现了在相反的方向的2种方式。年轻凡弗利特的方法是每个像素需要较少的算术运算。然而,不像Deriche的方法,两道不能并行处理。
用标准化滑动求和的误差评价两种方法的小标准偏差。当Deriche的脉冲响应更加准确时,年轻凡弗利特对随机噪声的图像处理更好。没有自然图像被检查。第五节提供了这些方法的进一步评价。
积分图像的基础方法。增量方法如方块过滤和区域求和表,也被称为积分图像。累计沿图像每行每列的像素值的总和。在这种方式中,一个矩形区域的总和,可以计算使用(1)的操作,其大小无关。这使得它用均匀核很快速的卷积一个图像是可能的。
Heckbert 广义积分图像的多项式d级d重复使用集成的内核,用于多项式逼近高斯核。沃曼介绍了另一种满足线性齐次的核的推广方程(LHE)。该方案要求d重复积分,其中d是LHE命令。侯赛因等人提出了非均匀滤波的核积分图像(KII)。所需的内核表示为一个简单函数的线性组合。每一个这样的函数的计算都独立使用卷积图像。为了证明他们的方法,作者用基于欧拉展开的多项式函数的线性组合逼近高斯核。类似的通过马里蒙曾提出了滤波方案结合线性函数形式的金字塔形核通道和elboher和沃曼,他使用的组合余弦函数近似高斯和Gabor内核和双边滤波器。
叠加积分图像。这个工作最相关的方法是Bhatia提出的叠加积分图像(SII)。作者通过叠加一个方块过滤器近似非均匀内核,即不变的二维矩形,这是所有从一个单一的整体形象计算。简单的使用的功能和不使用多个积分图像使得过滤效率很高。SII作者证明他们的方法对高斯积分的平滑。然而,他们只近似特殊的二维核,并发现为每个它们的局部极小非凸优化问题。虽然由此产生的近似结果可以重新调整,但他们是不准确的(见第五节)。此外,SII框架没有利用高斯内核的可分性。在本文中,利用可分性我们找到一个最佳的内核近似,可以缩放任何标准偏差。如图2所示,这种近似结果是更丰富、更准确。实际上,可分离的行和列K的一维过滤常数相当于2K -1二维盒。可分性特性也可用于有效的计算时间和空间,如在第三节描述的。
三 算法
A. 分段常数核分解
考虑核函数的卷积法。为简单起见,我们首先讨论的情况,K是一维的。在下面的(第iii-d)我们将讨论推广到更高的维度。
假定内核k的支撑是r,即k是在[0 ,r]范围外。假设我们给出了一个分区P =(P0,P1,hellip;Pk),其中0le; P0 lt;P1lt;P2hellip;lt; Pk-1lt;Pk le;r. 因此,通过结合简单的功能,核K可以用线性近似=Ki,i=1hellip;k:
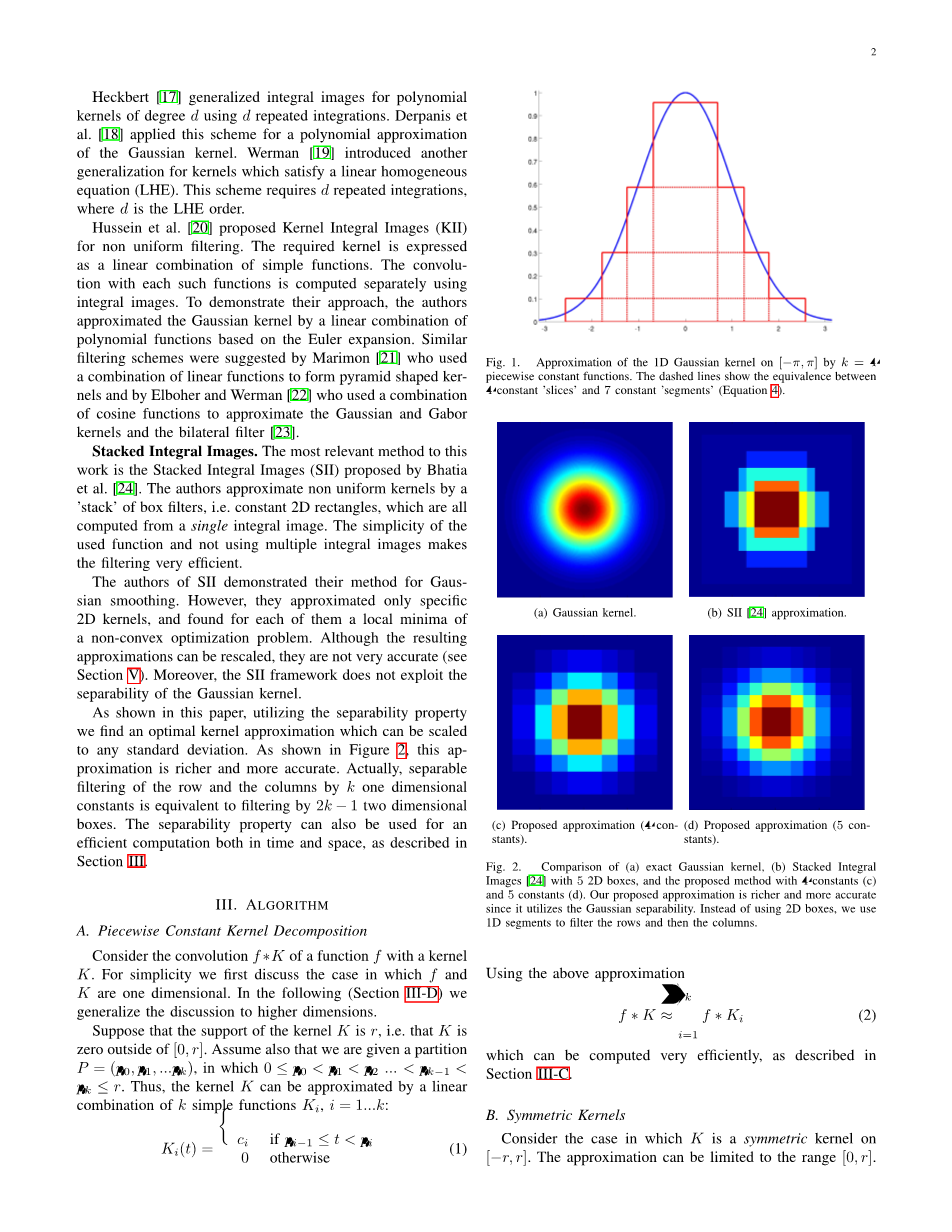
(a)高斯内核 (b)SII [ 4 ]逼近
(c)建议近似(4个常量) (d)建议近似(5个常量)
图2比较(a)精确的高斯核,(b)叠加积分的比较图像与5个二维盒,和所提出的方法有4个常数(C)和5个常数(D)。我们建议的近似更丰富,更准确。因为它利用高斯可分性。我们使用的不是二维盒,而是使用一段段来过滤行,然后一列列。
使用上述近似
这可以非常有效地计算,如第三部分c中描述的那样。
B. 对称核
考虑一下k是一个在[-r,r]对称的内核。近似可以被限制在[ 0 ,r]的范围内。
|
Method |
Additions |
Multiplications |
|
|
Direct |
h w 2 |
h w |
|
|
FFT |
O(log(hw)) |
O(log(hw)) |
|
|
KII [20] |
53 |
18 |
|
|
CII [22] |
12k 8 |
8k 8 |
|
|
SII [24] |
4k 1 |
k |
|
|
Deriche [7] |
8k 2 |
8k |
|
|
Young and |
4k |
4k 4 |
|
|
van Vliet [8] |
|||
|
Proposed method |
4k |
2k |
算术运算的每像素(第iii-d)
每一个恒定的Ci都可以使用在负区间[ -Pi ,-Pi-1]和在[ Pi-1,Pi],然而,这需要2K的常数函数。事实上,同样的近似可以计算使用“加权片”:
当omega;i=Ci-Ci-1,现在的内核是近似于非零的重叠的时间间隔[-Pi,Pi]总和的常数函数,与权重
omega;i=Ci-Ci-1。K的近似相同:
(4)
这一平等在图1中所示。
C. 一维滤波算法
在我们接下来的算法描述一个对称核K的情况(第III-B)。
给出了一维离散函数f(x)和K分段常数函数Si,我们计算近似卷积(公式2)如下
- 计算f(x),
(5)
(2)计算每个像素的卷积结果,
步骤1和2的总成本的增加是K 和2K情况下每个图像像素相乘。在一维的情况下,存储器访问不是一个问题,因为所有的元素通常都在缓存中。
D. 高维度和更多的计算方面
我们现在描述卷积二维图像f(x,y)的一个可分离的二维核K。这个内核K是可分离的如果它可以表示为一个一维滤波器卷积Kx*KTy。卷积f*k可以用第一卷积与Kx图像行和列的中间结果Ky计算,有可分离二维核的过滤图像只是一维情况计算成本的双倍。
空间复杂度也很低。因为每行Kx卷积(也是Ky每列)是独立的,过滤大小为(n*m)只需要O图像(max(n,m))是额外空间用于存储单行单列的累积总和的输入和输出的图像。
同样,在二维情况下,滤波方案可以扩展到高维的可分离内核使用2dk增加的和dk单像素的增加。需要额外的空间为O(maxi(ni)),ni(i=ihellip;d)是信号尺寸的大小。
表1计算了通过一个h*omega;的可分离内核二维图像滤波每个图像像素所需的操作。参数k表示的数(常量二维盒等)根据具体方法。注意,我们提出的方法与实验3常数比有5盒的SII 更准确,有一个类似于递归方法3系数的精度(第五节,图3(b))。这意味着我们所提出的方法比Deriche 要求更少的操作和所有基于积分图像的方法以及对年轻凡弗利特方法的一定数量的操作。
该方法也便于并行计算。求和的步骤(公式5)可以并行,在4.3节所描述的,而下一步(方程6)计算每个像素独立的响应。另一方面,递归方法可以并行部分如独立地过滤不同的行。然而,在每一行(或每一列),所有的计算都是强烈依赖不可独立的。
还注意到,方程6可以计算为图像像素的一小部分。这可以加快应用程序的内核响应采样窗口如图像缩小。递归的方法没有这种优势,因为它们是用它的邻近的内核响应计算每个像素的核响应。
四 核逼近
一维近似的内核K(t)K常数是函数通过P和常数Ci 隔开,通过在所需内核上最小化一个近似误差函数找到最好的参数。事实上,我们真正的目的是在输出图像上最小化误差,这未必是等价的。IV-A部分涉及核近似误差和利用自然图像统计输出的图像误差。我们定义一个二次型为内核的近似误差函数,所以输出图像二级误差最小化。此误差函数被用在IV-B部分去近似高斯核。
A. 最小输出二级误差
我们用x表示输入信号,用y表示输出信号,和用W表示核权重。近似输出和内核权重分别用和表示。上个字母X表示输入X的傅里叶变换。
最后的结果的平方的二级误差给出了
=(-)2
因为 =, 可以表示输入信号x和内核, ,
与输入信号x唯一相关的是内部总和,我们表示为Ajk=Xi j Xi k
标记 Ajk在位置j-k的x的自相关,这个误差可以被表示为
当A的条目为信号的自相关函数给出的X.
为了使E2独立的一个具体的值,我们利用自然图像的基本性质介绍傅立叶频谱的自然在每个频率的图像中,u与成比例。
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[29184],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。