英语原文共 4 页,剩余内容已隐藏,支付完成后下载完整资料
掺硼硅的极大磁电阻
JJHM Schoonus,FL Bloom,W。Wagemans,HJM Swagten和B. Koopmans
荷兰埃因霍温科技大学应用物理系,cNM
(2007年8月21日收到; 2008年3月27日发布)
制造硼掺杂的Si-SiO2-Al结构以研究极大的磁阻(MR)效应。电流 - 电压特性显示出非线性行为,其主要是碰撞电离的自催化过程。在低温下,磁场将碰撞电离的开始推迟到更高的电场。这导致在400kA /m时对称正MR超过10000%。与导纳光谱推导出的价带相比,施加磁场导致受主能级的增加。引入宏观传输模型来描述如何通过电压,电极间距和氧化物厚度来控制MR。
使用非磁性材料的半导体磁输运研究[1,2]是一个持续关注的领域。凭借其长自旋相干长度[4]和与当前CMOS技术的兼容性,硅对磁电子有着非凡的前景 [3]。在过去的几十年中,还研究了磁场对p型硅器件的影响。已经报道过微波频率下杂质传导区的负磁阻(MR)[5]和在跃迁机理[6]和电阻转变附近的FeSi-SiO2-Si结中的正磁阻(MR) [7]。也已经调查过磁场对二维电子系统中金属 - 绝缘体转变的影响[8]。然而,到目前为止观察到的最大磁阻(MR)在1T的典型场中仅为40%。尽管已经彻底研究过金属氧化物半导体异质界面中的非线性电传输 [9],但是对导致这种MR的机制的起源仍然缺乏共识。最近,研究表明,在半绝缘GaAs /i -GaAs /Au中,在宽温度范围内,在1T的磁场下电阻增加超过3个数量级,并且暂时归因于磁场依赖性雪崩击穿现象[10]。基于这种现象,观察以及对硅中较大MR的全面解释将是朝向新的自旋电子学应用的重要进展。
在这篇论文中,我们首次在掺硼硅中显示出远远超过10 000%的稳定的磁阻(MR),这与其他关于硅在更小磁场下显着更大的报道相反。通过系统研究用于在硅中注入载流子的薄二氧化硅层的作用(相当于参考文献中的肖特基势垒[10]),我们建立了理解增强磁阻效应的关键因素;隧道注入提供了所需的能量,以通过碰撞电离的自催化过程触发向高迁移率传输方式的转变。如Sladek所述,磁场提高了受体水平[11],并且以前报道过GaAs [12],通过GaAs用于碰撞电离的自催化过程的激活能量以指数方式增加,从而强烈抑制电流。
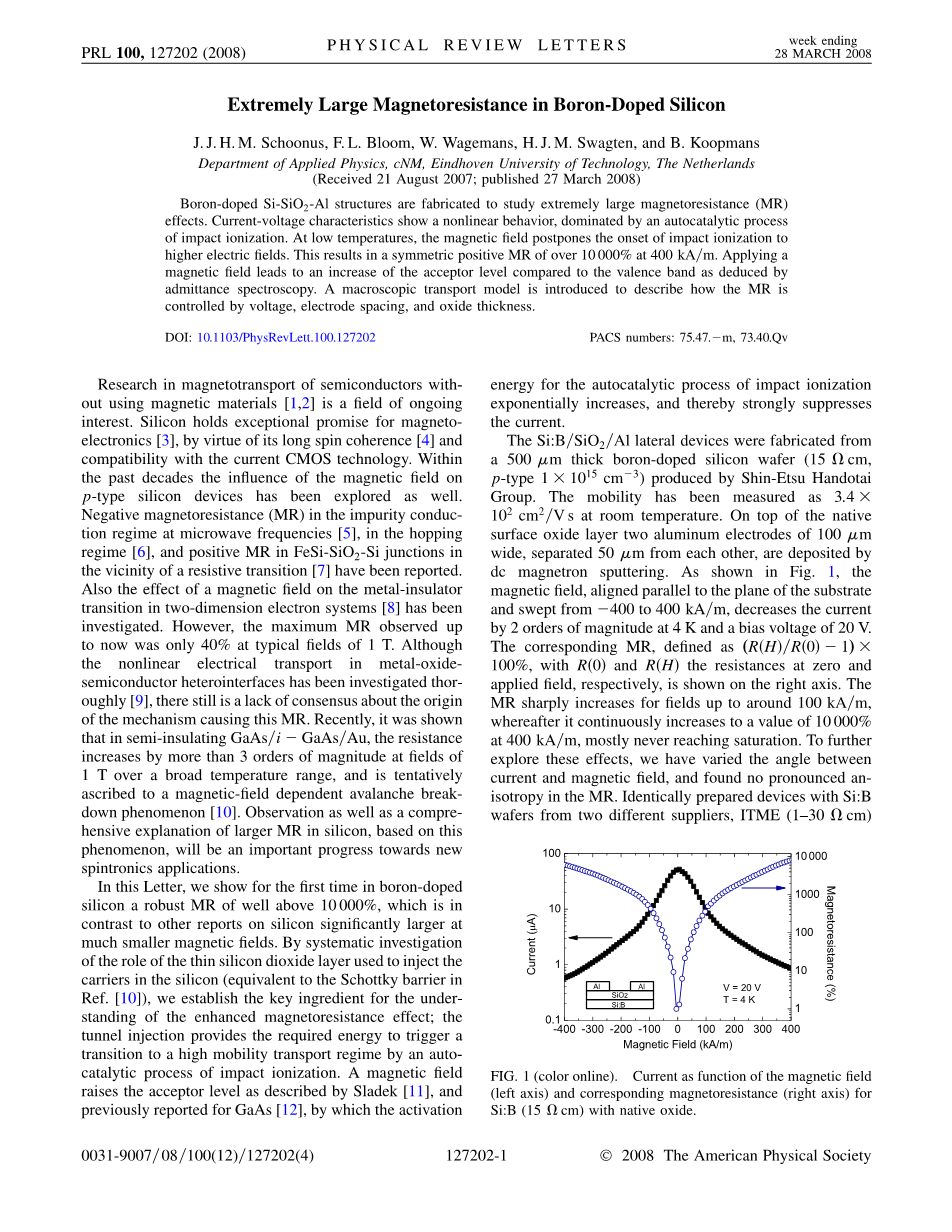
Si:B /SiO2/ Al横向器件由500mu;m厚的Shin-Etsu Handotai Group生产的掺硼硅晶片(15Omega;cm,p-type 1times;1015cm—3)制成。在室温下测量的迁移率为3.4times;102cm2/Vs.在自然表面氧化物层的顶部,通过DC磁控溅射沉积两个100mu;m宽的铝电极,彼此分开50mu;m。如图1所示,在4 K,偏置电压为20 V时,磁场平行于基板平面排列并从中扫过-400至400 kA / m,降低了电流2个数量级。相应的MR,定义为(R(H )/ R( 0)-1)times; 100%,R( 0)和R(H )分别表示零轴和外加磁场的电阻。对于大约100 kA / m的磁场,磁阻急剧增加,然后在400 kA /m时它连续增加到10 000%的值,大部分从未达到饱和。为了进一步探索这些效应,我们改变了电流和磁场之间的角度,发现MR中没有明显的各向异性。具有Si:B晶圆的相同制备的器件来自两个不同的供应商,ITME(1-30 Omega; cm)和Si-Mat(3-9 Omega; cm)表现出相似的行为,
图1电流作为磁场(左轴)和相应的磁阻(右轴)的函数,
Si:B(15 Omega; cm)具有原生氧化物。
可重复的电阻变化达8个数量级。这表明该效应是明显的,并且相应的机制应该与这些装置中的固有传输过程相关。
极大的MR效应如图1所示可以直接与高度非线性的电流 - 电压特性相关,这可以在各种磁场中观察到(见图2)。在插图中,给出了相同数据的对数线性图。电压在正方向上扫描并且在阈值电压(即,7V)下观察到电流急剧增加几个数量级。施加的磁场将该阈值电压推迟到更高的电场,并且曲线变得越来越陡峭。正如Sun等人所表明的那样[10],电流的急剧增加可以解释为浅受主硼的碰撞电离的自催化过程,并且阈值电压由热平衡中的费米能级和受主能级的相对位置确定。当电压在阈值电压下逐渐降低时,观察到与阈值电压相比较小的歇斯底里行为,表明碰撞电离的自催化过程可以维持在较低的偏置电压。这是MOSFET中离子碰撞模型的击穿模拟的一个众所周知的原理[13]。
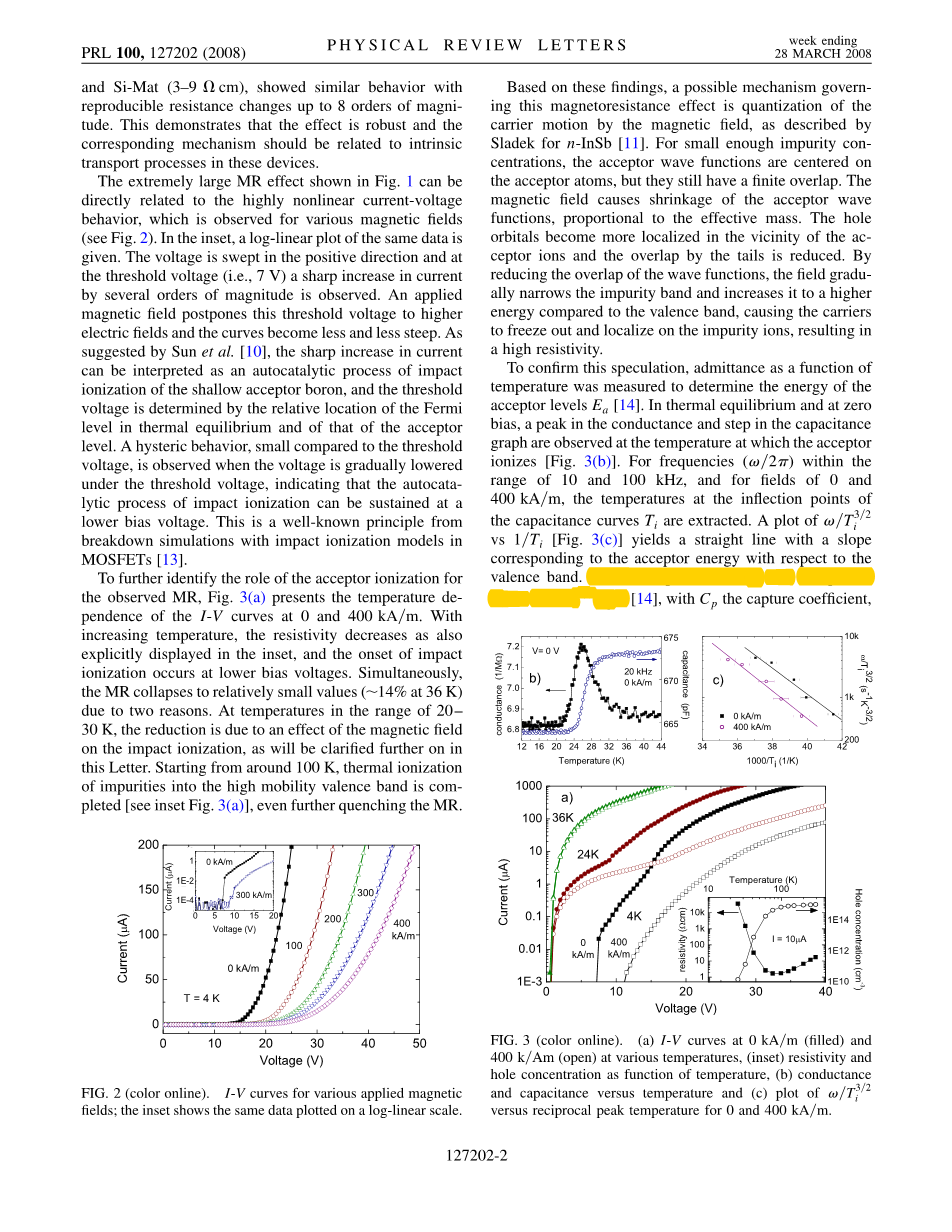
为了进一步确定受体电离对于观察到的MR的作用,图。3(a) 表示IV曲线在0和400 kA / m时的温度依赖性。如插图中明确显示的那样,随着温度的升高,电阻率也降低。并且碰撞电离的开始发生在较低的偏压下。同时,由于两个原因,MR坍塌到相对较小的值(在36K时为14%)。在20-30K的温度范围内,减小是由于磁场对碰撞电离的影响,这将在本论文中进一步阐明。从大约100 K开始,完成了杂质热迁移到高迁移率价带中 [图3(a)],甚至进一步降低MR。
图2各种磁场的IV曲线;
插图显示了以对数线性标度绘制的相同数据。
图3(a)在不同温度下0 kA / m(填充)和400 k / Am(开路)的IV曲线,(插图)电阻率和空穴浓度随温度的变化,(b)电导和电容与温度的关系(c)图w/ Ti3/2
相对于0和400 kA / m的倒数峰值温度。
基于这些发现,控制这种磁阻效应的可能机制是通过磁场量化载流子运动,如Sladek对n-InSb所述[11]。对于足够小的杂质浓度,受体波函数以受体原子为中心,但它们仍然具有有限的重叠。磁场引起受主波函数的收缩,与有效质量成比例。空穴轨道在受主离子附近变得更加局部化,并且尾部的重叠减少。通过减少波函数的重叠,该场逐渐使杂质带变窄并且与价带相比将其增加到更高的能量,导致载流子停止并定位在杂质离子上,导致高电阻率。
为了证实这种推测,测量温度影响的电导以确定受体能级Ea [14]。在热平衡和零偏压下,在受体电离的温度下观察到电容曲线中的电导和阶跃峰值[图3(b)]。对于10到 100 kHz范围内的频率(不等于2w),以及0到400 kA / m的磁场,提取电容曲线Ti拐点处的温度。曲线图w/ Ti3/2 vs 1 / Ti [图3(c)]产生具有相对于价带的受主能量的斜率的直线。1 / Ti = 0的截距等 于9.7 times; 1015me*3/2Cpbeta;二 [14],用Cp 捕获系数。这是电离受体捕获空穴的速率,并且可以使用有效质量me* =0.5和简并beta;=4。在零场中,我们推导出受体能量为(43.9 plusmn;0.2)meV。这与通过光电导测量的45meV的能量一致[15]。相应的捕获系数为(5.7plusmn;0.6) times;10-5 cm-3/s,这与通过掺硼5 times;1015cm3/ s研究得到的光电导和电流噪声值相当[16]。虽然图。3(b) 显示出对磁场的明显依赖性,但是难以分别提取Cp 和Ea 的依赖性。然而,我们已经证实对于浅受体(使用参考文献的分析[17])dCp/ dEa gt; 0。与价带相比,任何小的磁场引起的Ea 变化总是朝向更高的能量[11],这显然对应于Cp的增加。作为一种保守的方法,假设没有增加Cp 。因此,对于每个合理的受主能量,拟合的受主能量随着磁场的变化一致地移动至少1.8meV,导致空穴占据具有更高能量的状态。因此,碰撞电离需要更大的动能,对应于将阈值电压推迟到更大的电场(见图2)。最后,对于大于场依赖能量分裂的热能,其相对重要性降低,并且MR随温度而骤减,与图3(a)的观察结果一致。.
在我们的数据分析中,我们假设磁场对块硅中的载流子浓度有影响,而没有分析SiO2 的可能作用以及触点之间的间隔。因此,我们制备了样品,其中电极之间的间隔以及硅和铝之间的界面是变化的。首先,对于较大的电极间距,IV特性(未示出)中的阈值电压较高。尽管在恒定电流下测量的MR总是小于恒定电压MR,但它可以在很宽的电流范围内精确确定(图2)。恒定电流MR随着电极间距而增加,因此随着硅上的电压降而变化[图4(a)],但似乎到大约200%饱和了。
到目前为止,只有含有天然氧化物的硅晶片用于研究MR。在第二系列测量中,确定了SiO2 的作用。在用100mol /m3 HF浸渍去除自然表面氧化物层之后,制备具有不同界面的器件,即具有欧姆接触,没有SiO2的干净肖特基势垒,以及1.7nm和3.7 nm SiO2 层,其中厚度通过X射线光电子能谱测量。通过在450℃ 下在氩气氛中退火30分钟Al / Si界面获得欧姆接触,并且通过等离子体氧化在1times; 10—1mbar的压力,15W下制备SiO2 层。 正如预期的那样,具有3.7nm隧道势垒的SiO2 的器件对于进一步分析而言电阻太大。一个1.7nm的接近自然氧化物的厚度的SiO2隧道势垒的设备MR是最大的[图4(b)]。只有肖特基势垒(0 nm SiO2)仅在高电流下MR为20%,而对于欧姆接触,MR可忽略不计。从IV特性(未示出)可知,对于高偏压,具有宽能垒的器件的总电导低于具有小能垒的器件的总电导。这种行为是由于载流子的碰撞电离引起的体电阻降低引起的。我们得出结论,超薄屏障是产生大量MR效应的必不可少的成分,因为它有助于碰撞电离过程。
图4不同电极间距的恒流MR;
(a)400 kA / m时测量,(c)模拟和不同接触
(b)400 kA / m时测量,(d)建模。
为了阐明这些结果,可以制定一个简单的模型,该模型包括对碰撞电离过程的阻挡和体积贡献。我们推测这个过程是由空穴引发的,这些空穴从氧化物Vinj上的电压获得足够的动能以电离中性硼原子[18]。另外,硅中的电场必须足够大,使得加速的空穴自由地撞击其他空穴,并且持续撞击电离过程。
特定的电场和磁场中,我们考虑确定载流子密度p(E,H)的动力学过程的平衡。空穴浓度的变化率由下式给出:
. (1)
右侧的第一项表示空穴释放速率,而第二项表示电离受体捕获空穴的速率。在此,pa 是受体浓度。At 是热产生的载体产生率,估计为2times; 104s-1[19]。Ai 是碰撞电离系数,其计算类似于Cohen和Landsberg [20]作为受体水平和漂移速度的深度的函数,即在注入硅后,直接设定等于空穴速度,v =(2eVinj / m)1/2。按照参考文献[20],Ai 随着受体水平的深度呈指数下降。在热电子发射和隧道效应的通过屏障的电流,和硅上的电压成正比
. (2)
. (3)
用Js 表示通过势垒的饱和电流,mu;表示迁移率,l表示晶片的厚度,w表示电极的宽度,d表示电极之间的距离。来自方程式(1)–(3),对于恒定电流,器件上的总电压可以分别求解为0和400 kA / m。对于每个电流和磁场,假设p在整个硅中是恒定的。利用Js 作为每种类型的Al / Si界面的拟合参数,这导致MR行为,如图4(c) 和4(d),定性地跟踪我们的实验数据令人惊讶。数据可以通过应该满足的两个条件来解释以获得高MR。首先,MR与(V- 2Vinj) / V [见图4(c) 中左下方,电极间距的线性增加],最大的电压降应该超过硅片。一旦硅上的电压占主导地位,MR就会饱和[见图4(c),在右边]。其次,氧化物层上的电压降必须足够高,以向碰撞电离过程所需的载流子提供动能,该过程受到磁场的影响。通过增加电流或降低饱和电流来满足这一条件[见图4(d)],也因此Vinj 和MR增加。
最后,我们的模型显示,这种小的磁场引起的受体水平变化导致传导的急剧变化。从1.8 meV的受主能级变化(包括足够大的电压以引发碰撞电离),我们推断出碰撞电离系数的变化约为80%(使用参考文献的分析[20]),解释最大恒定电流MR的正确数量级。然而,极大的恒定电压MR应该通过方程式(1)中未涵盖的重组和电离之间的不平衡相互作用来描述。因为新发布的漏洞成为该过程的一部分。尽管如此,我们仍然认为我们的传输模型捕获了硅中大MR的相关参
全文共6890字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[2133]
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。