
英语原文共 7 页,剩余内容已隐藏,支付完成后下载完整资料
基于单模光纤模式干涉仪的折射率传感特性
张亚勋,周艾,秦伯阳,邓洪昌,刘志海,杨军,袁立波
摘要:我们对单模光纤模式干涉仪的折射率传感特性进行了理论和实验研究。理论分析表明,单模光纤中不同模式之间的干涉对外部介质的折射率变化有截然不同的响应。芯层与低阶包层模式之间的干涉降低折射率灵敏度,而芯层与高阶包层模式之间或两种不同阶包层模式之间的干涉增加折射率灵敏度。采用大芯阶跃折射率多模光纤迈克尔逊干涉仪进行了实验验证。在基于单模-多模-单模的迈克尔逊干涉仪中,多模光纤作为一个模耦合器来激发单模光纤中的包层模。分别在氯化钠水溶液中测试了多模光纤不同长度的单模-多模-单模结构的折射率响应。实验结果与理论分析吻合良好。
索引词:包层模式、光纤模式干涉仪、光纤传感器、折射率灵敏度。
1.介绍
基于单模光纤(SMF)的光纤模式干涉仪作为折射率(RI)传感器,由于包层模式对周围介质折射率变化的依赖而具有特别的吸引力。各种不同的结构已经被报道用于构建测量折射率的模式干涉仪。其中包括突变锥对[1]、[2]、核偏置拼接[3]、[4]、双包层光纤[5]、光纤布拉格光栅(FBG)[6]、长周期光栅(LPG)[7]、[8]和芯径失配[9]-[13]。如果我们注意这些报告的折射率敏感性,我们可以发现一些调查中的折射率敏感性为负[1]、[3]-[5]、[7]、[12],而另一些调查的折射率敏感性为正[2]、[6]、[8]-[11]。其中,负正的折射率敏感性意味着蓝红波长随着外部的折射率增加而偏移。更有趣的是,即使是对于类似的构型[7][8][11]-[14]折射率敏感性也可能相反。我们认为这种现象如上述文献中,由于激发了不同的包层模式,这些包层模式对外部折射率有不同的响应。此外,大多数文献中,包层模式间的干扰被忽视了,只考虑了芯层模式和包层模式之间的干涉。然而,尤其在基于单模光纤的模式干涉仪中,很难仅激活单模光纤中的一种包层模式,不同包层模式之间的干涉对模式间的折射率灵敏度起着重要的作用。但遗憾的是,在我们所知范围内,还没有详细研究包层模式对模式干涉仪折射率灵敏度的影响。
在本文中,我们尝试用单模-多模-单模迈克尔逊干涉仪来解释折射率灵敏度的符号反转现象,并对基于单模光纤的模式干涉仪的折射率传感特性进行了一般描述。单模-多模-单模结构与多模光纤(MMF)作为传感光纤、单模光纤作为传输光纤的单模-多模-单模结构完全不同。在本研究中,传感光纤为单模光纤, 多模光纤作为模耦合器在传感单模光纤中同时激励芯层模式和包层模式。采用这种结构的原因是多模光纤-单模光纤结构比其他包层激励方法更容易激发高阶包层模式。此外,还可以通过改变多模光纤的长度来调整被激发包层模式的阶数。事实上,首次提出多模光纤-单模光纤结构激发包层模式是用于温度传感领域,[11]、[12] 这类结构的折射率响应早已经报道了 [13]-[16]。然而,在参考文献中。只给出了某些包层模式的折射率响应,没有研究包层模式阶数对干涉仪折射率传感性能的影响[13] -[16]。此外,在[13]和[14]中的结构敏感性与[15]和[16]中的相反。因此,在本研究中,我们主要研究包层模式对基于单模光纤的模式干涉仪折射率灵敏度的影响。通过选择两个不同长度的多模光纤,212um和2.1mm,在传感单模光纤中,不同顺序包层模式会被激发,正面和负面折射率敏感性两种都被获得。
论文组织如下。在第二部分,我们简要介绍了单模-多模-单模迈克尔逊干涉仪,给出了基于单模光纤的模式干涉仪折射率灵敏度的一般解析表达式。在芯层-包层模式干涉和包层模式间干涉的情况下,我们分别定义与模式色散相关的折射率灵敏度系数了。通过分析,芯层和包层模式对波长的依赖于有效折射率关系(ERI), 多个包层模式(HE11minus;HE1,16)折射率灵敏度系数被算出,结果表明,芯层模式与低阶包层模式的干涉信号系数为负,而芯层模式与高阶包层模式或包层模式之间干涉呈正关系。在第三部分,我们对不同多模光纤长度结构折射率敏感性进行了实验研究。实验结果验证了折射率敏感性的理论预测。在第四部分,我们对基于单模光纤模式干涉仪的折射率响应给出了一个概括性的结论。
2.折射率灵敏度的理论分析
A.基于单模-多模-单模结构的芯-包层模式干涉仪。
通常,基于单模光纤的模式干涉仪的折射率灵敏度主要由包层模式决定,因为它对周围介质敏感。因此,为了全面研究模式干涉仪对外部介质的响应,在传统单模光纤中,我们必须对包层模式进行尽可能多的激励。虽然包层模式可以通过突变锥度、核偏置拼接、小芯径差和光纤光栅等多种方法容易激发,但这些方法只能激发一种或几种包层模式。同时获得足够的低阶和高阶包层模式是困难的。由于阶跃指数多模光纤具有均匀的指数分布和较大的芯直径,可以在多模光纤-单模光纤剪接区域激发大量的包层模式。更重要的是,改变多模光纤的长度可以改变单模光纤的激励光场,这可能导致不同的包层模式的激发。因此,在本研究中,我们选择了基于单模-多模-单模结构的迈克尔逊干涉仪作为传感头。
图1 基于单模-多模-单模的迈克尔逊干涉仪原理图
基于单模-多模-单模的迈克尔逊干涉仪原理图如图1所示。短段多模光纤被拼接在两个单模光纤之间。一单模光纤作为导入/出光纤为光路传输,另一个剥去包层的单模光纤作为传感元件。传感单模光纤的末端被小心地切开,然后涂覆一层金色薄膜作为反射器。在单模-多模-单模结构中,由于模场失配较大,多模光纤起着模耦合器的作用,将导入/出单模光纤的基本芯层模式耦合到传感单模光纤的基本芯层模式和包层模式中。这里,单模光纤是传统单模光纤由长江光纤公司制造和纯石英芯多模光纤是一个功率传输光纤(Nufern MM-S105/125 - 22)芯/包层直径的105/125mu;m和数值孔径为0.22。多模光纤的大芯径可以保证传感单模光纤中高阶包层模式的激励。为了在多模光纤-单模光纤剪接点获得不同的入射光场,激发不同的包层模式分布,选取多模光纤切片长度分别为0.2 mm和2.1 mm左右。所有的光纤都是在“Auto SM/NZ/DS/MM”操作模式下用Fujikura电弧熔接机(FMS-60S)进行熔接的。
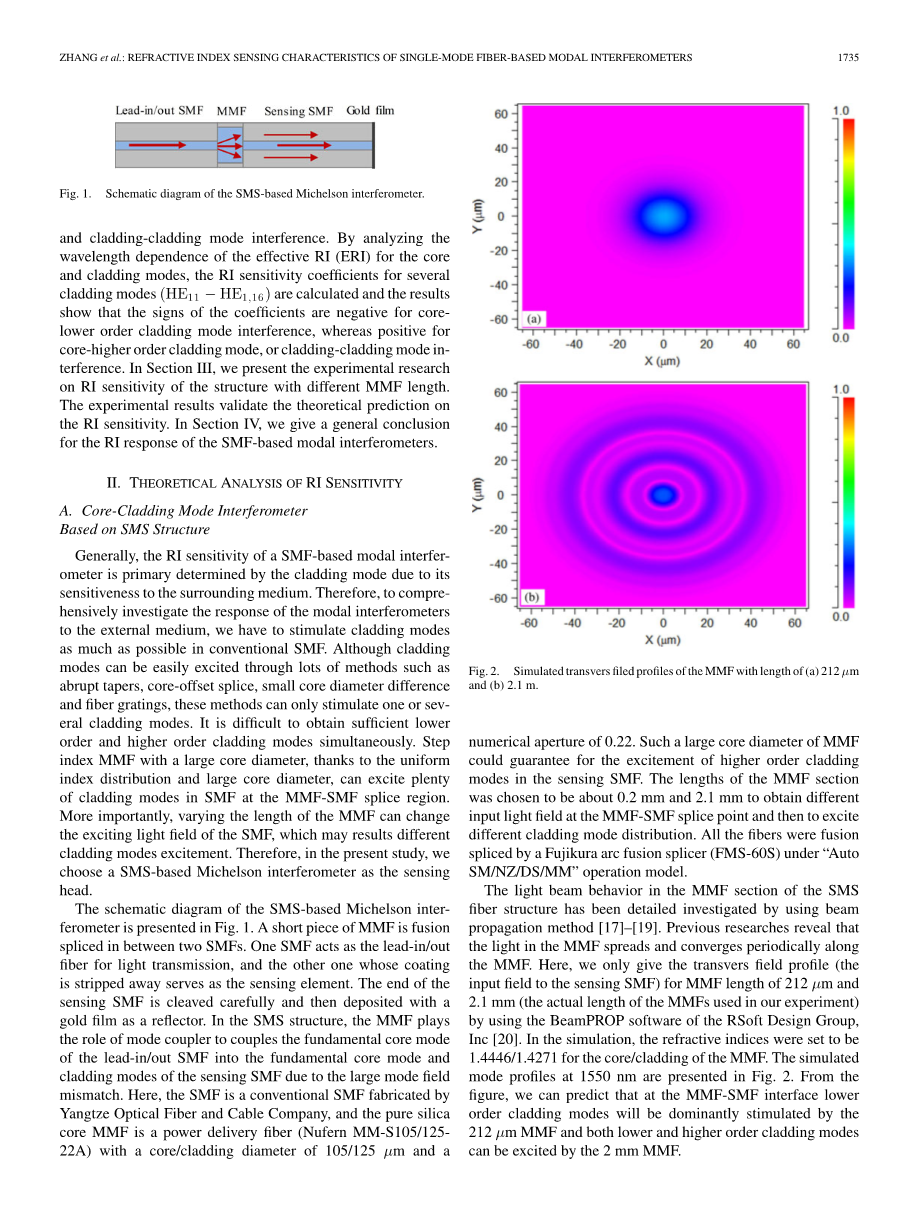
采用光束传播方法[17]-[19]对单模-多模-单模结构中的多模光纤段的光束行为进行了详细的研究。以往的研究表明,多模光纤中的光沿多模光纤周期性地扩散和收敛。在这里,我们通过使用RSoft设计集团公司[20]的BeamPROP软件只给出212mu;m和2.1mm长度的多模光纤横向场分布(传感单模光纤的输入段) (我们实验中多模光纤用的实际长度)。在模拟中,多模光纤的芯/包层折射率设置为1.4446/1.4271。图2给出了1550 nm处的模拟模式分布。从图中,我们可以预测,多模光纤-单模光纤界面,212mu;m 多模光纤主要激发低阶包层模式,2mm多模光纤激发低阶和高阶包层模式。
图2 多模光纤的长度212mu;m (a)和(b) 2.1mm模拟横向场轮廓
B.折射率敏感性
首先,我们考虑了基本芯层模式与m阶包层模式之间的干涉。破坏性干扰引起的传输倾角
满足相位条件[9]
(1)
其中和分别为基本芯层模式的ERI和m阶包层模式,L为传感单模光纤的长度,为外介质的折射率, 为第i个角的波长,i为整数。需要注意的是和都是波长的函数。有效指数的波长依赖性是由材料和波导色散引起的。随后将会显示,基本芯层模式与包层模式的ERI之差是决定灵敏度符号的关键参数。在这里,由于材料几乎相同,可以假设材料的色散对和有相同的影响,而波导色散是色散差的主要因素。
由(1)得到某一确定角 的波长可以表示为
(2)
对分别对外部折射率 B求导,得到透射角的折射率灵敏度的解析表达式
(3)
其中
(4)
定义x为芯层-包层模干涉的灵敏度系数。其中,为芯层模与m阶包层模的有效指数差,和为芯层模模与m阶包层模外部折射率的波长依赖关系。对于(4)的右边,和总是正的,因此x的符号由分母决定其符号取决于项。
为了定量分析其灵敏度,计算了芯层模和部分包层模的外部折射率。对于图1中的传感单模光纤,考虑到周围介质,它是一个三层结构。因为单模光纤的包层直径远远大于芯层直径,为简单起见,所建立指导模式的感应单模光纤引入到计算的是两层模式,而不是三层结构:一个由传感单模光纤的芯层和包层组成,计算HE11包芯模式,另一个是由传感单模光纤的包层和周围介质组成,计算HE1m包层模式。这两个模型的精确解可以在参考文献[21]中找到。
图3 芯层模式和几种包层模式的外部折射率的波长依赖关系。
芯层模式和包层模式的波长从1mu;m-1.6mu;m范围的外部折射率绘制在图3中。从上到下的曲线,对应的是芯层模式和、、、、、包层模式。这里,包层模式的径向数从第一个包层模式开始,而不是从芯层模式开始。在计算中,芯层和包层的直径和折射率被设置分别为8.2um,125mu;m,1.449和1.444。从图2我们可以看到,对于低阶包层模式我们有(),而对于高阶的包层模式有() .因此对于那些大于的包层模式,灵敏度系数x是负的。对于高阶包层模式,存在两种情况:和,对于第一种情况,x仍然是负的,对于第二种情况,x变为正。
事实上,(4)也可以写成的格式为
(5)
从分母上看,与群指数差在形式上相同,其中,和分别为芯层模式和m阶包层模式的群指数。从(5)中, x的符号只取决于的符号, 这与[22]中液化石油气的分析结果相吻合。
在实际应用中,在单模光纤中只激励一个包层模式是困难的,而基于单模光纤的模式干涉仪中的干涉通常是多模式干涉。因此,必须考虑两种不同阶包层模式之间的干涉。对于两个包层模式干涉,透射角的折射率灵敏度为
(6)
其中为第j(jlt;m)阶包层模式的外部折射率, 定义为包层模式干涉的灵敏度系数,表达式为
(7)
和对应于第一个16阶 包层模式在波长为1550纳米的计算结果,展示在表1。
表1 计算了前11种HE1m模式的折射率灵敏度系数
从表1中的计算结果,对于芯层-包层模式干涉,当包层模阶数mle;10时,折射率灵敏度系数是正的,当包层模阶数mgt;=11时,折射率灵敏度系数是负的。对于包层-包层模式干涉,灵敏度系数总是正的。由式(3)和式(6)可知,干涉仪的折射率灵敏度由各模式的外部折射率的灵敏度系数和依赖关系决定。因此,为了确定折射率灵敏度,计算了几种包层模式下外部折射率的外部折射率依赖关系,结果如图4所示。从图中,我们可以看到,每个包层模式的外部折射率随着外部折射率增加,这意味着。而且,高阶包层模的外部折射率比低阶包层模式的外部折射率增加的快,这表明(mgt;j)。因此,从(3)中,芯层-包层模式干涉的折射率灵敏度,当mle;10时是负的, mge;11时是正的,从(6)中,包层-包层模式干涉的折射率灵敏度总是正的。因此,基于单模光纤的多模干涉仪的最终折射率灵敏度由包芯模式干涉和包层模干涉两者共同决定。因此,灵敏度不仅取决于被激发的包层模式,而且取决于模式的功率分布。也就是说,不同的激励模式之间的功率分布可能导致不同的灵敏度。
图4 几种包层模式的外部折射率依赖关系。
为简单起见,我们考虑一个简单的情况下,芯层模式以及两种包层模式(mle;10)传感单模光纤的激发。有两种极端条件下:和(,和 分别是芯层模式和两个包层模式的能量)。在第一种情况下谱的形状是由芯模和包层模之间的干涉决定的,包层-包层模干涉对谱的调制较小,因此灵敏度主要表现为负的。在第二种情况下,光谱的形状是由两种包层模式之间的干涉决定的,芯-包层模式的干涉对光谱有轻微的调制,这导致了正灵敏度。在其他情况下,有些是正的,而对另一些则是负的。为了直观地说明功率分布和外部折射率对波长漂移的影响,模拟了芯层模式和包层模式和之间的干涉。计算结果如图5所示。图5(a)为:: = 0.45:0.1:0.45的情况,图5(b)为:: = 0.1:0.45:0.45的情况。从图5中我们可以看到,第一种情况下所有波长透射衰减的都发生了蓝移,第二种情况下发生了红移。一般来说,对于两种包层模式被激发的情况,灵敏度主要由能量相近的模式决定对于包层模式较多的情况,灵敏度比较复杂,很难对折射率灵敏度进行一般描述。
图5 当外部RI为1.34和1.36时,包层模式和,芯层模式的受激干涉光谱(a)和(b)
三.实验结果与讨论
A.基于单模-多模-单模结构的迈克尔逊干涉仪的光谱特性
在传感单模光纤获得不同的分布包层模式,两个基于单模-多模-单模的迈克尔逊干涉仪(单模-多模-单模1和单模-多模-单模2)与制造了长度为 212mu;m和2.1毫米的多模光纤。将单模-多模-单模结构中的传感单模光纤的长度设计为相同的(20 mm),以便于比较单模-多模-单模结构的光谱特性。将波长范围为1520 nm至1610 nm的宽带光耦合到导入/出单模光纤中,利用光学频谱分析仪(OSA)检测反射干涉光束。两个干涉仪的干涉光谱如图6所示。从图中可以看出,这两种干涉图都是不均匀的,这说明有不止一种包层模式被激发并与传感单模光纤的芯层模式发生干涉。即便如此,我们仍然可以清晰地观察到干涉条纹的间隔随多模光纤长度的增加而减小。
图6 具有不同长度的MMF的SMS迈克尔逊干涉仪的透射光谱,(a)212mu;m和(b)2.1 mm
图7 具有不同长度MMF的SMS迈克尔逊干涉仪的空间光谱
为了更直观地显示参与干涉的包层模式,将图6中的频谱傅里叶变换到空间频域,如图7所示。每个频谱的多峰验证了包层模式被激发并参与干涉的预测。单模-多模-单模2中的包层模数量大于单模-多模-单模1中的包层模数量。此外,单模-多模-单模2中高阶包层模的功率比单模-多模-单模1中高阶包层模的功率大。两种光谱的差异是由多模光纤的长度差异引起的传感单模光纤的输入
全文共8614字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[1195]


