利用区域映射相移干涉法进行快速局部波前校正
- 前言
我们提出了一种全新的基于面积映射相移干涉法的局部波前校正方法。在这篇论文中,我们提出了这个理论,然后通过实验将其与先前演示的基于光斑优化相位步进(sops)干涉法的方法进行了比较。我们发现AMPS在速度方面比SOPS干涉法快三倍,尽管在噪声环境中改进可能更大。AMPS产生的点扩展函数(PSF)与用于中度系统诱发像差的SOP相似,但对于较大像差产生的点扩展函数稍不理想。本文中描述的方法可能显现出对于相位步进解决方案没有足够速度这一问题的关键作用。copy;2011美国光学学会
- 正文
光学系统经常会出现象差,使振幅和分辨率降低到理想点扩散函数(PSF)预测的值以下。通常,校正的第一步是获得畸变波前图。对于某些应用,这是容易接近的,可以使用波前传感器(WFS)进行采样。在许多光学系统中,这是不可能的。例如,在多光子激光扫描显微镜(MPLSM)中,荧光场景的强度在信号上取决于焦距[1]。当光通过光学不均匀组织时,不同的光线产生不同量的延迟,特别是高数值孔径物镜时。为了解决这一问题,非确定性算法被用于搜索相位校正空间,以优化特定指标,如荧光强度[2–4]。然而,由于时间和镜像变形性的限制,通常只探测到较低的频率,因此这些可能在高空间频率相位变化时失败。其他方法使用WFS[5,6]从聚焦区域对背散射光的波前进行了采样,其缺点是背散射光束从介质种传播,不能完全代表聚焦点的状态。
近年来,确定性方法已被发展用于像差校正。Vellekoop等人通过改变空间光调制器(SLM)的每个像素的相位来优化CCD相机上的单个像素,从而实现了通过组织的最佳光传输[7]。Čižmaacute;r等人和Ji等人分别对光捕获[8]和MPLSM[9]应用了相关技术。最后,Bowman等人演示了一种敏感的方法,利用一个SLM作为一个棚屋-哈特曼WFS来显示一个焦点网格来测量和纠正像差[10]。
在本文中,我们分析了Čižmaacute;r等人和Ji等人提出的技术。在傅立叶光学方面,演示了一种基于相同仪器的全新的更快速的方法。我们强调两种方法都在一个位置优化焦点。这一点很重要,因为当通过畸变介质(如混浊生物样品)聚焦时,不同的点可能需要不同的校正[8]。
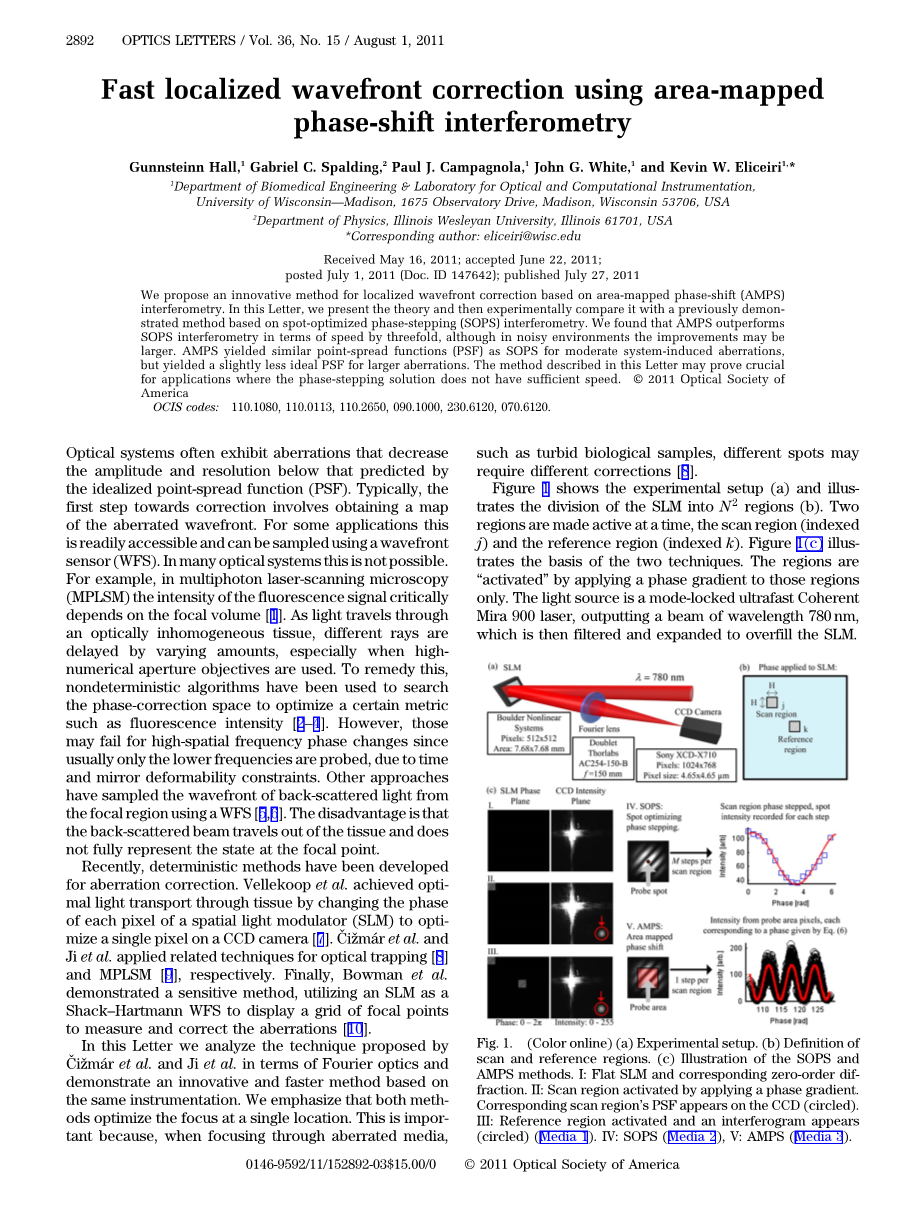
图1显示了实验设置(A),并说明了SLM划分为区域(B)。一次激活两个区域:扫描区域(索引J)和参考区域(索引K)。图1(c)说明了这两种技术的基础。这些区域仅通过对这些区域应用相位梯度来“激活”。光源是一个锁模超高速相干mira 900激光器,输出波长780nm的光束,然后对其进行过滤和扩展,使SLM充满。
本文提出了用傅立叶光学分析[8,9]方法的理论框架,在此基础上建立了新的方法。目标平面(SLM)光场[参见图1(b)]可写作:
应用傅立叶变换,图像平面(在CCD上)的辐照度为
这里我们定义(为了简化运算)
其中h是区域高度,dx和dy是扫描区域和参考区域之间的水平和垂直距离。函数表示干涉图可见的窗口,相位梯度参数tx和ty控制其位置。
我们称之为光斑优化相位步进(sops)波前校正法的方法只在扫描区域增加了一个相位。该相位从0阶跃至2pi;,单位为m阶跃,记录点()处的强度作为扫描阶段的函数,然后可以写为
通过拟合余弦项,可以确定相位偏移:
等同于最佳相位选择,使扫描和参考区域达到相位的拟合,是最佳聚焦的条件。通过迭代移动扫描区域并找到每个区域的相位偏移,可以找到整个SLM的相位图。SOPS方法的一个缺点是,它要求每个区域至少有三个相位步数m,以完全采样余弦函数。但是,更多的步进(以及数据点)会提高相位图的精度,因此速度较慢。
我们建议使用图像平面中的空间变化相位(创建干涉图[图1(c)v),而不是步进扫描区域的相位,以获得校正。这种方法将被称为面积映射相移(AMPS)方法。
为了利用这一信息,我们将等式(2)中余弦的空间变化相位项组合成一个单相项,如下所示:
探头区域内的每个像素都有一个相关值a和一个强度值。作为空间变化相位函数的强度可写为
通过将拟合到余弦,我们发现_a_拟合frac14;minus;Delta;_,通过与式(5)比较,我们得出
由于该方程中的所有项都已知,因此可以计算相位偏移。通过对所有区域重复此操作,可以获得整个SLM的校正图。两种方法的运行时间这样给出
在我们的设置中,每次迭代的时间约为55ms(18hz),对应于4times;4、8times;8和30times;30区域校正的0:88s、3:52s和49:5s,分别对应于AMPS(mfrac14;1)。相应的SOP校正需要至少三倍的时间才能实现优化。
为了验证,我们将AMPS与SOPS方法进行了比较。图2显示了随着区域数量的增加(增加波前细节)校正系统像差的结果。图2(a)显示了从两种方法中获得的波前。图2(b)显示了我们新方法的结果。图2(c)描绘了PSF峰值强度随波前细节增加而增加的情况。AMPS和SOP的峰值强度分别增加了83%和82%。此外,图中显示了全宽半最大值(FWHM)内像素的平均强度,并与峰值强度成相同变化趋势。最后,在图2(d)中,显示了PSF的径向轮廓,并与理论系统的径向轮廓进行了比较。这两种方法都具有几乎达到衍射极限的性能。
为了评估AMPS以校正较大的像差,我们在聚焦透镜前面插入一个像差玻璃[图3(a)]。两种校正方法均采用900(30times;30)区域,图3(b)显示了恢复的波前。图3(c)显示了对应于无校正(n/c)(Ⅰ)、安培校正(Ⅱ)和标准操作程序校正(III)的PSF。此外,图3(d)显示了径向剖面,并与理想系统剖面进行了比较。如果不进行校正,PSF的扩散性很强,强度很弱。AMPS和OPS都提供了显著的改进,并且与理想的系统配置文件相当。值得注意的是,在这种情况下,SOP的峰值强度比AMPS高23.74%。在PSF宽度(或分辨率)方面,由于像素大小的限制,我们的设置无法解决实验误差范围内的差异。
参考文献
1. W. Denk, J. H. Strickler, and W. W. Webb, Science 248,73 (1990).
2. P. N. Marsh, D. Burns, and J. Girkin, Opt. Express 11,1123 (2003).
3. M. Booth, M. A. A. Neil, and T. Wilson, J. Microsc. 192,90 (1998).
4. S. P. Poland, A. J. Wright, and J. M. Girkin, Appl. Opt. 47,731 (2008).
5. M. Rueckel, J. A. Mack-Bucher, and W. Denk, Proc. Natl.Acad. Sci. USA 103, 17137 (2006).
6. J. W. Cha, J. Ballesta, and P. T. C. So, J. Biomed. Opt. 15,046022 (2010).
7. I. M. Vellekoop and A. P. Mosk, Opt. Commun. 281,3071 (2008).
8. T. Čižmaacute;r, M. Mazilu, and K. Dholakia, Nat. Photonics 4,388 (2010).
9. N. Ji, D. E. Milkie, and E. Betzig, Nat. Methods 7, 141 (2009).
10. R. W. Bowman, A. J. Wright, and M. J. Padgett, J. Opt. 12,124004 (2010).
通过计算生成的多焦点衍射
1. 前言
多焦点光学元件在诸如具有调节能力的眼内透镜,激光光盘头,3-D图像形成系统的应用中有着重要的作用。文中提出的生成多焦点衍射的计算方法,已经用于在特殊类型相位非线性的基础上计算菲涅尔型多焦点透镜。多焦点镜头表示为薄透镜和非线性失真菲涅耳透镜的数学叠加。在此前提下,我们将非线性类型的选择归结为具有预定阶间能量分布的相位衍射光栅的槽形确定问题。特别的,我们已经对双焦点镜头和七焦点镜头进行了研究。
2. 介绍
为了多焦点的问题,我们使用分段衍射光学元件[1,2],它们的孔径由具有不同焦距的一组适当的衍射透镜型区段组成。 由于孔径段的配置彼此不同,因此在分段透镜的焦点中图像分辨率,出射光瞳的形式和视场是不同的。另一种方法是利用二元菲涅耳波带片的众所周知的多焦点特性[3]。 然而,这些区域平板不允许人们控制焦点之间的能量分布并形成预设数量的焦点。本文的主要贡献是推出了一种用于合成高效多焦点镜片的衍射方法,它们具有所需的焦点数量并且满足它们之间的预设功率分布。
- 多焦点镜头的阐述
计算生成的相位衍射透镜给人以实现光束的任意相位延迟的机会。 众所周知[3],对于薄光学元件,区域内有限高的相位纹理可以对很大范围变化的相位函数起到相位延迟的作用。在这种情况下,纹理高度与将相位函数模除2pi;后的数值成比例,并通过这些纹理高度生成相位变化。我们用此部分包含相位函数的计算来描述多焦点衍射透镜的透镜,能够得到将照明光束(波长为)转换成具有预定功率比的N个点的在光轴上的聚焦分布。
本节包含描述多焦点衍射透镜的相位函数的计算。 透镜必须以预定的功率比将入射光束(波长,)聚焦到分布在光轴上的N个点上。
(如图一所示)
图一
众所周知,任何非线性的相位都会产生额外的衍射级。 如果应用于菲涅耳透镜的相位,那些非线性预失真会产生几个焦点。 例如,二元菲涅尔波带片,是相位透镜的硬限幅型非线性应用的结果,给出了无限的焦点组。 然而,在这种情况下,照射光束功率无用地聚焦在不希望的焦点上。 必须强调的是,非线性类型确实影响了焦点之间的能量分布。 作者提出了选择特殊类型非线性的方法,用以确保在预定数量的焦点之间所需的能量分布。
让我们将多焦点镜头表示为具有以下区域相位菲涅耳型镜头:
这里(u)是入射镜头的光束的相位,u =(u,v)表示镜头平面中的正交笛卡尔坐标系中的坐标.函数
是镜头的近轴相位,两镜头分别具有焦距f1和f2。(u)这一项是用来补偿入射光束的相位。透镜相位(u)代入等式(1)起到沿光轴选择焦点坐标的作用。函数使透镜1的相位减小到[0,2x]的范围内。函数描述了相位(u)的非线性预失真(参见图2)。例如,任意每个周期具有个切口的达曼光栅都可以生成二元相位区域板。这种波带片具有个环而不是传统二元相区带板的每个环。因此,多焦点镜头描述为传统镜头(u)和非线性预失真的数学叠加。区域板可以是二阶或高阶梯度,或者甚至在区域中具有连续的非线性扭曲的微浮雕轮廓。我们将具有相位(1)的镜头称为“扭曲相位”镜头。
让我们考虑多焦点镜头(1)用于产生光强为光束的情况。薄的多焦点镜头的相位在光学上被添加到入射光束的相位(u)(在不变的幅度下)。因此我们可以在紧接着镜头平面后的位置写下以下形式的场:
图二 非线性映射关系变换
为了描述多焦点分布情况,让我们将函数在[0,2pi;]上做傅里叶级数展开得到如下(4)(5)式:
其中傅里叶展开的系数满足:
将代入到(4)式中并以2pi;为周期展开我们能将等式(3)写作如下形式:
我们可以将表达式(6)解释为一组具有焦距为
并且它们之间的功率分布为的近轴球面光束的叠加。
让我们假设,...,是与多焦点镜头设计中所需焦距相对应的索引,所以这就足够让我们在区间[0,2pi;]上定义一个函数,它的傅里叶级数展开(5)满足以下等式:
作者已经提出将预失真解释为具有周期2pi;和以,...,为顺序光强为,...,的N阶衍射光栅的相位函数。这种解释将多焦点透镜计算的问题减少到相位衍射光栅合成的众所周知的问题,其中衍射级之间具有预设的功率分布 [6,7,8]。 应该提到的是,衍射光栅是这里只是一个虚拟光栅。 它不是叠加在镜头上,而是仅用作数学点对点非线性处理。
- 双焦点镜头的计算和研究介绍
作为一个重要的例子,我们将考虑焦距为,的双焦镜头合成,并且每个焦点具有相等的功率。 孔径G是圆形的,半径为R. 在这种情况下,我们将,= ,= 代入表达式(7)中对于“扭曲相位”多焦点镜头的焦距,得到:
此外,我们将非线性预失真函数定义为二阶衍射光栅的相位函数:
按(4)的方法得到傅里叶展开的系数按如下所示:
并且。因此,超过81%的照明光束功率集中在系数l=1和l=-1的展开中。将等式(9),(11)代入等式(6),其中l =plusmn;1为非零项,得到平面照射光束下输出光场的下列表达式:
等式(12)描述了聚焦到两点(在近轴近似中)的所需过程。 我们已经对由“畸变相”双焦透镜形成的场强进行了计算机模拟,其依照等式(1),(2),(9),(10)相位函数。将其
全文共7301字,剩余内容已隐藏,支付完成后下载完整资料

英语原文共 11 页,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[274],资料为PDF文档或Word文档,PDF文档可免费转换为Word


