
英语原文共 7 页,剩余内容已隐藏,支付完成后下载完整资料
具有磁性和电性的单体硅纳米筒的光学光谱分析 声波
由高指数半导体或介电材料制成的纳米颗粒的共振电磁特性对于实现新型纳米天线和超材料是非常有希望的。在本文中,我们研究了位于二氧化硅衬底上的Si纳米圆柱体的光学共振。多极分析的实验散射光谱的多极分析,基于分解的离散偶极子近似,证实了硅纳米柱中电和磁偶极模式的共振激发。光的影响研究了光的极化和入射角对纳米基体散射特性的影响。结果表明纳米基体中电和磁模式的共振激发对入射角和光的偏振的依赖性允许入射角和光的偏振,可以控制和操纵该系统的散射光。这些所展示的硅纳米柱的特性可用于实现具有不同功能光学特性的电介质元表面不同功能的光学特性.
从米氏理论中可以看出,电介质粒子的第一和第二最低共振对应于磁偶极和电偶极项。对于更高的折射率,这些米氏共振的质量系数和它们的光散射效率会增加。由于这些特性,高折射率的介质颗粒被认为是创造具有负有效磁导率和介电常数的超材料的有希望的构件。据报道,介电超材料在微波和中红外频率下具有很强的磁和电反应的实验证明。最近,从理论上预测了硅球形纳米粒子在可见光谱范围和红外区域的强磁和电偶极共振响应,并在实验中得到了证明。利用硅纳米粒子的这些光学特性,人们提出了新的全介质光学纳米天线和光学超材料。最近,理论上和实验上表明,硅纳米粒子的电和磁偶极共振的光谱位置可以通过改变其形状来调整。例如,有可能通过改变硅纳米片的长宽比,在相同的光学频率上激发电和磁偶极共振。纳米片通过改变其长宽比来激发电偶极共振。这种可能性允许通过使用硅纳米盘或纳米盘来控制光散射特性。
这种可能性允许通过使用具有明确尺寸参数的硅纳米片或纳米圆柱体来控制光散射特性。这就是为什么最近对圆柱形介质纳米颗粒的光学特性进行了深入研究的原因之一。实验证明,在基底上制作的硅纳米圆柱体的二维周期性阵列,支持米氏共振,在所有可见光谱范围内产生几乎零的总反射。理论上考虑了位于不同基底上的圆柱形硅纳米颗粒的光学共振,并由正常入射光波照射。米氏共振对周期性硅纳米圆柱体阵列中的光吸收的影响已在文献中得到实验证明和研究。在本文中,我们从实验和理论上研究了位于二氧化硅基底上的单圆柱形硅纳米粒子的光学共振特性,并讨论了其对光吸收的作用。
激发的多极模式在其消光和散射光谱中所发挥的作用。同时还研究了光的偏振和入射角对散射图的影响。
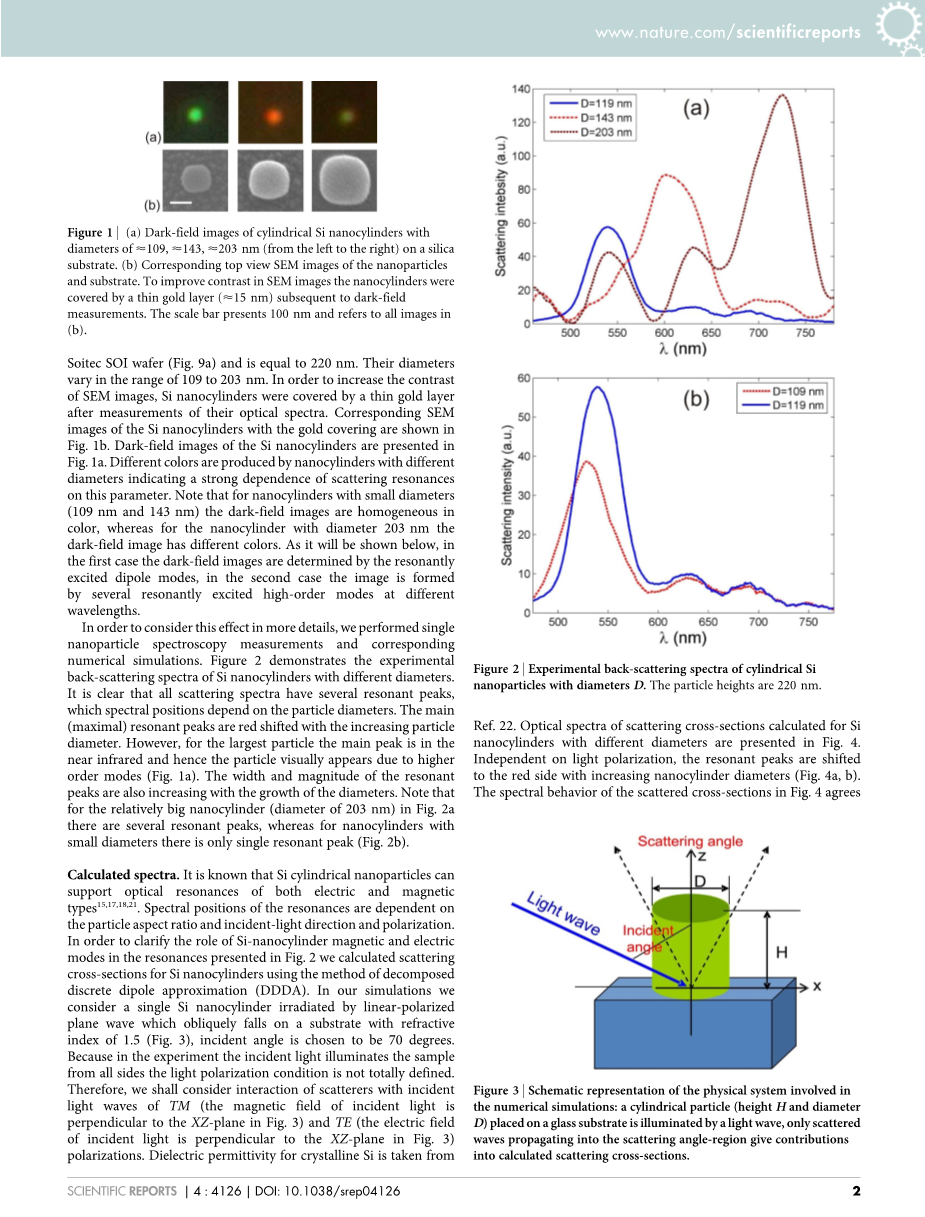
图一:(a) 在硅基上直径为asymp;109, asymp;143, asymp;203 nm(从左到右)的圆柱形硅纳米圆柱体的暗场图像。(b) 相应的纳米颗粒和基底的俯视SEM图像和基底的相应俯视SEM图像。为了提高SEM图像的对比度,在暗光测量之后,纳米颗粒被一层薄薄的金层(lt;15纳米)所覆盖。比例尺为100纳米,指的是(b)中的所有图像。
结果
图1显示了位于二氧化硅衬底上的制造的硅纳米圆柱体的扫描电子显微镜(SEM)图像。所有纳米圆柱体的高度由Soitec SOI晶圆上的硅层厚度决定(图9a),等于220纳米。它们的直径在109至203纳米的范围内变化。为了增加SEM图像的对比度,在测量了它们的光学光谱后,Si纳米颗粒被一层薄薄的金层所覆盖。图1b显示了有黄金覆盖的硅纳米圆柱体的相应的SEM图像。图1a中显示了硅纳米柱的暗场图像。不同直径的纳米圆柱体产生不同的颜色,表明散射共振对这个参数有很强的依赖性。请注意,对于小直径的纳米柱(109纳米和143纳米),暗场图像是同色的,而对于直径203纳米的纳米柱,暗场图像有不同的颜色。如下所示,在第一种情况下,暗场图像由共振激发的偶极子模式决定,在第二种情况下,图像由不同波长的几个共振激发的高阶模式形成。
为了更详细地考虑这种效应,我们进行了单纳米粒子光谱学测量和相应的数值模拟。图2展示了实验性的不同直径的Si纳米颗粒的背散射光谱。很明显,所有的散射光谱都有几个谐振峰。其光谱位置取决于粒子的直径。主要的(最大的)共振峰随着颗粒直径的增加而发生红移。然而,对于最大的颗粒来说,主要的峰值是在近红外,因此颗粒在视觉上是由于高阶模式而出现的(图1a)。共振峰的宽度和大小也随着直径的增加而增加。请注意,对于图2a中相对较大的纳米圆柱体(直径为203纳米),有几个共振峰,而对于小直径的纳米圆柱体,只有一个共振峰(图2b)。
图2--直径为D的圆柱形Si纳米颗粒的实验性背向散射光谱。粒子高度为220nm。
图3-数值模拟中涉及的物理系统示意图:一个圆柱形粒子(高度H和直径D)放在玻璃基板上被光波照射,只有传播到散射角区域的散射波才有贡献。贡献到计算的散射截面中。
计算光谱
众所周知,硅圆柱形纳米粒子可以支持电和磁两种类型的光学共振。共振的光谱位置取决于粒子的长宽比和入射光线的方向和偏振。为了澄清图2所示的Si纳米柱磁和电模式在共振中的作用,我们使用分解离散偶极子近似(DDDA)的方法计算了Si纳米柱的散射横截面。在我们的模拟中,我们考虑由线性极化的平面波照射单一的硅纳米柱,该平面波斜落在折射率为1.5的衬底上(图3),入射角被选择为70度。因为在实验中,入射光从四面照射样品,光的偏振条件不完全确定。 因此,我们将考虑散射体与入射光波的TM(入射光的磁场垂直于图3中的XZ平面)和TE(入射光的电场垂直于图3中的XZ平面)极化的相互作用。结晶硅的介电常数取自文献。图4显示了对不同直径的Si纳米柱计算的散射截面的光学光谱。独立于光的偏振,共振峰随着纳米柱直径的增加而转移到红色一侧(图4a,b)。共振的光谱位置也是独立于光的偏振的。例如,对于D=150纳米的纳米圆柱体,第一个共振的主要区别是图4a和4b所示的第一个共振之间的主要区别仅在于其两个肩部的相对值(在TE极化情况下,lambda;= 675纳米的第二个肩部比TM极化情况下更明显)。这种趋势对于直径较小的纳米圆柱体是保持的。然而,对于直径为D= 90 nm的纳米圆柱体,这种差异大大减少(图4c),散射截面与图2b中的实验光谱一致。尽管图2中的实验光谱和图4中的理论数据在质量上是一致的,但还是有明显的差异。由于在制造过程中在硅纳米粒子上产生了一个小的氧化壳,我们实验中的纳米圆柱体的直径要比模拟中的大。因此,硅纳米粒子的有效尺寸,这决定了共振的位置在实验中减少了。
为了澄清图4中主要谐振峰的来源,我们将多极分解应用于散射电场,并将针对纳米圆柱体的不同多极矩分别计算的散射截面与一般散射截面进行比较。在我们的模拟中,我们计算了纳米圆柱体相对于其质心的多极矩。图5显示了直径为100纳米的Si纳米管的这种比较结果。第一个低频共振(波长lambda;=590纳米)对应于纳米柱的磁偶极(MD)矩的激发,与光的偏振无关。图5a中的肩部和图5b中的峰值在相同的lambda;=540纳米处,基本上是由纳米胶体的电偶极(ED)矩决定。在TE极化的情况下,MD散射截面有两个共振峰,对应于纳米柱MD的平面内分量(lambda;= 590 nm)和平面外分量(lambda;= 520 nm)的共振激发。请注意,一个磁四极(MQ)共振出现在两个极化的宽ED和MD共振的背景上。它对计算的散射光谱的影响相对较弱。图5中总散射截面和多极散射截面的共振峰位置之间的差异是由多极场对散射角80°计算的总散射截面的干扰贡献来解释的,如图3所示。
尽管图4中显示的不同光偏振的散射截面有一定的相似性,但在多极激发方面有重要的区别。在大入射角的倾斜光入射下,光激发的主要偶极子成分是TM极化的面外(z-)分量和MD的面内(x-)分量,反之则是TE极化。由于平面外的偶极子不会正常辐射到基底表面,所以散射角相对较小的散射截面(图3和图4)基本上由ED和MD的平面内分量决定。因此,我们看到图4a和4b中的相应散射截面有相似之处。如果考虑到全消光和全(向所有方向)散射截面,这种情况就会发生明显的变化。从图6可以看出,TE极化情况下的消光和散射截面的值比TM极化的小得多。在后者的情况下,ED矩的主要(平面外)成分和唯一(面内)分量是共振的被同一波长区域的光激发,增加了消光和散射(图6a)。在TE极化的情况下,主要的(面外)分量(lambda;= 520 nm)和面内分量(lambda;= 5 0 0 nm)的共振。面内分量(lambda;=590 nm)的MD矩共振是在ED共振之外实现的。在ED共振之外实现(图6b)。此外,平面内的ED分量对消光和散射截面的贡献在图中也是如此。图6b中的散射截面比图6a中的平面外ED分量的贡献要小得多,这是因为圆柱形纳米材料的ED极化性的相应分量之间的差异。圆柱形纳米粒子的偏振性张量之间的差异。比较图中的消光和 比较图6中的消光和散射截面,可以看到相对的光对TM极化的吸收较弱。
图4 散射角为80度的锥形区域内的散射截面的计算光谱(图3)的硅纳米圆柱体。(a) TM极化光平面波的散射。(b)TE偏振光平面波的散射。(c) 对TM极化和TE极化入射光计算的直径为D=590 nm的Si纳米柱的散射截面(SCS),绿色曲线是对偏振平均的计算。所有纳米柱的高度等于220nm,入射角度等于70度。光的波长。
图5 - 散射角为80度的Si纳米管在(a)TM偏振和(b)TE偏振的光波照射下进入锥形区域的总散射截面的计算光谱(图3)。纳米圆柱体的直径等于100nm。其他参数见图4。图中还显示了对纳米柱的不同多极矩分别计算的散射截面呈现。ED - 电偶极;MD - 磁偶极;EQ - 电四极;MQ - 磁四极。
图6 - 计算出的全消光光谱和散射截面的Si纳米管被(a)TM偏振和(b)TE偏振的光波照射。纳米圆柱体的直径等于 为100nm。其他参数见图4。贡献 纳米圆柱体的电偶极(ED)和磁偶极(MD)矩的贡献 对消光截面的贡献也被列出。
入射角的影响。
图5中计算的Si纳米管的消光截面是入射角的函数。图5中作为入射角和波长的函数计算的Si纳米管的消光截面在图7中展示了两个偏振的情况。可以看出,对于小的入射角(从0到30度),两个偏振的消光光谱非常相似。由波长为520纳米和590纳米的光激发的主要共振分别对应于纳米柱的面内电偶极矩和面内磁偶极矩。对于大于30度的入射角,存在着主要的差异。对于TM极化光,lambda;=590纳米处的截面开始增加,在入射角60度左右达到最大值(图7a)。这种效应是由散射体的平面外电偶极和平面内磁偶极矩的增加所解释的。请注意,这两种偶极子模式的共振波长是重合的,但平面外电偶极子共振明显比磁偶极子共振宽(图6a)。对于大于75度的入射角,由于总入射电场和磁场的强烈减少,所有的共振都变得很弱(在这个角度区域,两个极化的反射系数接近,因此总的外部电场和磁场接近零)。相反,在TE极化的情况下(图6b),消光(散射)截面的谐振值随着入射角的增加而减少。
电和磁的共振激发的依赖性偶极子模式的共振激发对入射角和光的偏振的依赖,允许控制和塑造系统中的散射光。图8展示了在固定入射角度下通过改变偏振来改变光散射模式的可能性。对于TM极化,有一个强烈的不对称散射到基底(图8a),由于Si纳米管的共振激发的面外电偶极矩和面内磁偶极矩产生(散射)场之间的干扰。它呈现了位于玻璃基底上的Si纳米柱的Kerker型散射。在TM极化的条件下,对于大的入射角,我们有一个情况,在质量上类似于当硅纳米盘被线性偏振光正常照射的情况。在这些条件下,电偶极子和磁偶极子共振可以在同一光谱区域被激发(如图6a所示),由于电偶极子和磁偶极子散射场之间的干扰,导致了高度定向散射图案。请注意,在两个具有失谐电偶极反应的金属纳米粒子系统中可以观察到类似的不对称的电磁场分布。在TE极化情况下的对称散射模式(图8b)是由磁偶极矩的面内分量决定的。图8中白色虚线圈外的黑色区域,当theta;gt;pi;/2是禁光区,由临界角决定,theta;c=pi;-arcsin(1/n2)asymp;138°,其中n2是基底的反射指数。
图7-图5(高度为220纳米,直径为100纳米)的Si纳米圆柱体的消光截面(mu;m2),作为入射角和波长的函数计算(a)TM极化和(b)TE极化的入射光。(a)中的箭头显示了偶极子模式,它对消光截面有主要贡献。虚线对应于图6中的消光光谱。箭头表示相应多极矩的谐振贡献。
结论
综上所述,实验证明,直径在109至203纳米范围内的圆柱形硅纳米粒子在二氧化硅衬底上有220纳米的高度。203纳米,高度为220纳米的圆柱形硅纳米粒子放置在二氧化硅基底上具有在可见光谱范围内有共振的光学反应。基于分解的离散偶极子近似的理论分析表明,硅纳米圆柱体的光学特性是由它们的磁和电偶极决定的。被入射光激发。随着纳米筒直径的增加,偶极子共振被转移到红外区域。传播方向和入射光的波长对 考虑了传播方向和入射光波长对Si纳米圆柱体的电和磁模式的共振激发的影响。主要关注的是 当电偶极模式和磁偶极模式在可见光谱范围内被共振激发的情况 在可见光谱范围内被激发。它已经证明了 总消光和散射截面以及散射指向性在很大程度上取决于Si纳米柱的方向 相对于光的入射方向和它的偏振有很大的关系。研究发现,散射光的指向性可以由入射光的偏振来操纵 散射光的指向性可以由入射光的偏振来操纵,这是因为电偶和磁偶的同时谐振 由于Si纳米柱的电偶极和磁偶极模式的同时共振激发,散射光的指向性可以被入射光的偏振所操纵。所展示的硅纳米基体的光学特性可用于 可用于实现多功能的介电元表面和光学器件,用于纳米天线和传感应用。进一步的研究将集中在基于高阶多极模式的共振激发的硅纳米柱的光学特性上。
图8|以球面坐标显示的散射指向性(a.u.),对图3所示系统进行计算:高度为220纳米、直径为100纳米的硅纳米管被波长为590纳米的光平面波照射,入射角为65度。极性角theta;isin;[0,pi;]由径向距离表示,而方位角theta;isin;[0,2pi;]则显示在图中平面。圆的中心theta;=0对应于基体上方的法向散射;圆的边界h 5 p对应于进入基体的法向散射。基材上方(下方)的散射对应于白色虚线圈内(外)的区域,对应于theta;=pi;/2。(a)
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[604052],资料为PDF文档或Word文档,PDF文档可免费转换为Word


