
英语原文共 5 页
基于保偏布拉格光纤光栅的法布里-珀罗干涉传感器
摘要 - 光纤布拉格光栅(FBG)已被用作传感器头,用于测量温度和静态应变。然而,在单模光纤上构建的标准FBG传感器在两者兼有的条件下都不能很好地工作,温度和应变因传感器而独立变化他们之间的交叉敏感性。 交叉敏感问题可以通过使用在保偏光纤(PM-FBG)上构建的FBG代替标准FBG来解决。 在本文中,我们报告了同时测量温度和静态应变的分辨率的改进,介绍了用PM-FBG(PM-FBG-FPI)构成的法布里-珀罗干涉仪作为传感器头。 PM-FBG-FPI反射的精细结构光谱可以实现波长漂移的高分辨率检测。通过实验证明了所得到的高分辨率测量结果。
索引术语——法布里 - 珀罗干涉仪,光纤布拉格光栅,光纤传感器
I. 介绍
因为FBG传感器有重量轻,体积小,抗电磁干扰等的优点,FBG传感器已被广泛使用[1]–[3]。FBG反射特定波长的光,该反射波长,称为布拉格波长,会因为温度变化或施加的应变而发生变化。该布拉格波长偏移可用于测量温度,应变,声压和固体振动。然而,因为FBG传感器具有温度变化和应变之间的交叉敏感性,传感器不能在温度和应变均独立变化的条件下使用。
为了克服这种交叉敏感性问题,国内外已经提出并使用了各种测量方法。 组合多个光栅可以区分温度变化并应用应变[4]。 FBG纤维内短Fabry-Perot腔也可以用于同时测量温度和应变[5],[6]。 使用写入高双折射光纤的FBG还可以同时测量温度和应变[7]- [9]。 一些着有特殊结构的FBG[10],[11]被提出作为传感器头同时测量温度和应变。
用于同时检测两个被测量的光纤光栅传感器的测量分辨率,最小可检测变化往往低于为单个被测量设计的FBG传感器的测量值。例如,在上述同时测量方法中,使用Duet al提出的传感器,温度分辨率最高达到的是0.3。[5] 但该传感器的应变分辨率低至30mu;ε。由Patricket al [4]提出的方法,提供最高的应变分辨率9mu;ε和1.5的低温度分辨率。采用目前基于光纤光栅的同步测量方法,均无法同时获得温度和应变高测量分辨率。
通过将不同的传感技术与基于光纤光栅的传感相结合,可以改善同时测量的分辨率,以换取FBG传感器的一些优点。一个典型的例子是,组合了FBG传感器和稀土掺杂光纤传感器的组合传感器[12]。 该传感器的分辨率为0.3和4.9mu;ε。但是,由于该传感器长度是FBG传感器长度的十倍,因此其空间分辨率低于FBG传感器的空间分辨率。此外,光纤只能包含一个组合传感器,而许多FBG传感器可以放在光纤中。
最近,我们提出了[13]基于FBG的高分辨率传感器,可同时测量温度和静态应变。我们使用法布里-珀罗干涉仪构造了两个FBG,这两个FBG用保偏光纤(PM-FBG-FPI)作为传感器头。 在PM-FBG-FPI中,在PM-FBG的反射光谱中出现尖锐的透射率峰值。PM-FBG-FPI反射光谱的精细结构能够实现波长漂移的高分辨率检测,其性能与FBG法布里-珀罗干涉仪一样[14]- [17]。
在本文中,我们描述了PM-FBG-FPI传感器的细节。 为了精确表征PM-FBG-FPI,我们改进了实验装置,以稳定PM-FBG-FPI周围的温度,并在PM-FBG-FPI上施加精确的静态应变。改进的设置也用于实验证明温度和应变的同时测量。
II.原理
PM-FBG有两种类型的反射光谱[7]。FBG的反射率达到最大值的Brag波长,由光栅周期和有效折射率决定。由于保偏(PM)光纤具有对应于两个正交偏振分量的两个折射率,因此如果FBG被写入PM光纤,则FBG具有两个布拉格波长。
使用两个布拉格波长,PM-FBG可用作同时测量温度和应变的传感器。两个布拉格波长对温度和应变有不同的依赖性。假设布拉格波长对应较高的折射率是,对应于较低折射率的布拉格波长是。 ,,温度变化Delta;T和施加应变ε之间的关系由下式给出:
(1)
(2)
其中和是温度变化和应变应用之前的布拉格波长,而,,和分别是温度变化和应用应变的波长漂移系数。因此温度变化Delta;T和施加应变ε可以通过下式获得:
(3)
具有高双折射的法布里-珀罗干涉仪是通过写入两个相隔一段距离的FBG来构造PM光纤[18]。然后干涉仪(PM-FBG-FPI)在其反射光谱中具有尖锐的透射率峰值。
这个高峰由对应于两个折射率的两组组成。使用两组透射率峰值可以实现高分辨率同时测量。当PM-FBG-FPI周围的温度变化和/或应变施加在PM-FBG-FPI上时,峰经历波长漂移。对于这些峰值,波长偏移系数为温度变化和应用的应变与布拉格波长相同PM-FBG。因此,使用类似于Eq(3)的等式,温度变化和施加的应变可以通过测量峰的波长偏移来确定。由于透射峰值的带宽窄于来自PM-FBG的反射峰值的带宽,因此可以以高分辨率估计峰值的波长偏移。因此,通过使用PM-FBGFPI传感器,可以预期温度和应变的高分辨率同时确定。
III. 实验和结果
PM-FBG-FPI是通过两个长度为1mmPM-FBG制造的,FBG之间的距离为10mm。PM-FBG-FPI的总长度为12 mm。 通过用相位掩模将紫外光曝光到PM光纤上来进行制造。PANDA纤维(Fujikura SM15-PS-U25A)用作PM纤维。
图1显示了用于表征制造的PM-FBG-FPI的实验装置。光源是波长可调激光二极管,调谐分辨率为0.1 pm。调节来自光源的入射光的偏振状态使用偏振控制器以均衡两个偏振分量的量。通过使用光纤耦合器将入射光分成两部分。
图1.实验装置。 TLD:可调谐激光二极管; ISO:光隔离器;PLC:偏振控制器; FC:光纤耦合器; PD1:用于输入的光电探测器监测; PD2:用于测量透射光的光电探测器
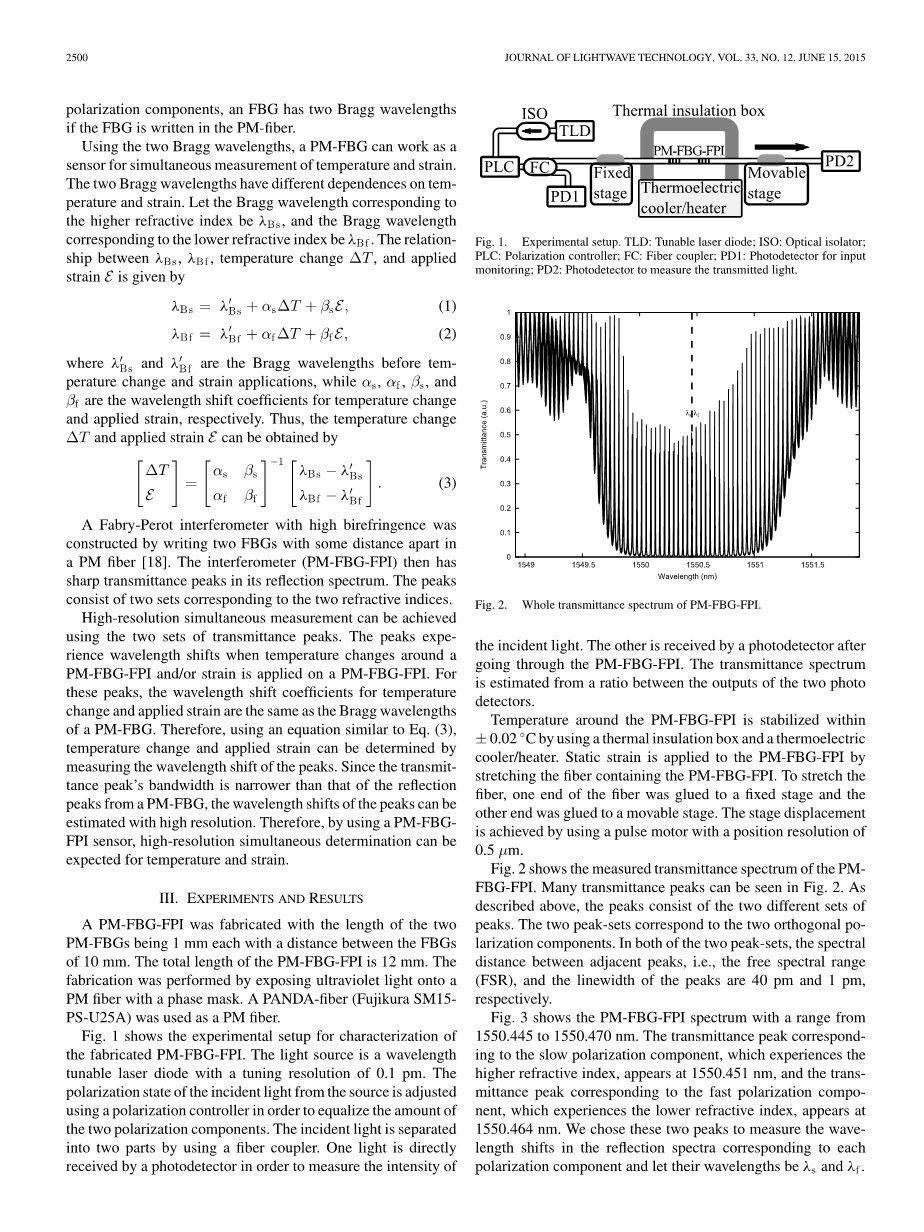
图2. PM-FBG-FPI的整个透射光谱
光检测器直接接收一束光,以测量入射光的强度。另一部分的的光是在通过PM-FBG-FPI后由光电探测器接收的。根据两个光电检测器的输出之间的比率估计透射光谱。
通过使用隔热箱和热电冷却器/加热器,PM-FBG-FPI周围的温度稳定在。通过拉伸含有PM-FBG-FPI的纤维将静态应变施加到PM-FBG-FPI。 为了拉伸纤维,将纤维的一端粘合到固定台上,将另一端粘合到可移动台上。 通过使用位置分辨率为0.5mu;m的脉冲电机实现平台位移。
图2显示了PMFBG-FPI的测量透射光谱。 在图2中可以看到许多透射率峰值。如上所述,波峰由两组不同的峰值组成。两个峰值组对应于两个正交偏振分量。在两个峰值组中,相邻峰值之间的光谱距离,即自由光谱范围(FSR)和峰值的线宽分别为40pm和1pm。
图3显示了PM-FBG-FPI光谱,其范围为1550.445至1550.470nm。对应于经历较高折射率的慢偏振分量的透射率峰值出现在1550.451nm处,并且对应于经历较低折射率的快速偏振分量的透射率峰值出现在1550.464nm处。我们选择这两个峰来测量对应于每个偏振分量的反射光谱中的波长偏移,并使它们的波长为和。
为了评估PM-FBG-FPI的温度依赖性,我们将PM-FBGFPI周围的温度从30改为80°C,使用热电冷却器/加热器以10°C为步长。我们在温度变化期间测量了两个峰值波长和。对于每个实验条件,峰值波长测量进行十次。
图4显示了温度依赖性测量的实验结果。在图4中,清楚地显示了两个峰值波长随温度变化线性移动。我们还显示了峰值波长之间的差值在图5中。可以看出差值增大与温度升高成比例。这是因为对应于慢速的峰值的波长偏移
偏振分量小于对应于快轴偏振的峰值。波长漂移从结果得到的系数和alpha;f是10.15plusmn;0.01和10.56plusmn;0.01 pm /°C
图3.PM-FBG-FPI光谱,范围为1550.445至1550.470nm
图4.温度变化与峰值波长的变化
图5.温度变化与峰值之间的波长差异
图6.应用的应变与峰值波长的变化
对于PM-FBG-FPI的应变依赖性测量,移动阶段逐步从0以100微米的步长移位到1000mu;m。由于光纤末端之间的初始距离为1米,因此施加的应变从0到1000mu;ε变化。我们在应变变化期间测量了两个峰值波长和。对于每个实验条件,峰值波长测量进行了十次。
图6显示了应变测量的实验结果。清楚地表明,波长随着施加的应变的增加而线性增加。我们还显示了图7中峰值波长lambda;f鈭舍difference之间的差异。可以看出,差异与增加的应变成比例地减小。这是因为对应于慢偏振分量的峰值的波长偏移大于对应于快轴偏振的峰值的波长偏移。如果在PM-FBG-FPI上施加超过1000mu;ε的应变,则图7中所示的差值可以为零并且达到负值。从该结果获得的波长漂移系数和为1.1870plusmn;0.0008和1.1784plusmn;0.0008pm /mu;ε。
我们通过实验证明可以使用PM-FBG-FPI同时测量温度和应变。在该实验中,施加在光纤上的静态应变分别为0,100,200和300mu;ε,PM-FBG-FPI周围的固定温度为40°C。我们在应变变化期间测量了两个峰值波长lambda;s和位置f。 然后在50和60℃的温度下重复相同的步骤。对于每个实验条件,峰值波长测量进行十次。
测量结果如图8所示。均方根值测量误差为0.5和5mu;ε。测量误差由式(3)中所用的波长系数和峰值波长的检测误差决定[19]。在此前的工作中,Omichi[9]等人报道提出用单个PM-FBG传感器工作,波长系数几乎相同,我们的PM-FBG-FPI传感器以及系数如下:
,,且。对于PM-FBG传感器,测量误差为plusmn;2和plusmn;20。因此,实验结果表明,从峰值波长的检测中减少了测量误差。
4.结论
我们提出了一种用于高分辨率同时测量温度和应变的新型PM-FBG-FPI传感器。我们已经评估了制造的PM-FBG-FPI的透射光谱及其对温度和应变的依赖性。PM-FBG-FPI具有良好的透射率峰值。峰值由对应于两个正交的两组峰值组成偏振分量。对于两个峰值集,FSR线宽分别为40和1 pm。通过实验获得两个峰值组的波长偏移系数分别为10.15plusmn;0.01和1.1870plusmn;0.0008为峰值设定对应于慢极化,10.56plusmn;0.01和1.1784plusmn;0.0008对于与快速极化相对应的峰值组。使用PM-FBG-FPI同时测量温度和应变已经通过实验证明。测量误差的rms值分别为0.5°C和5mu;ε。这些结果实验证明,所提出的PM-FBG-FPI传感器具有0.5°C和5mu;ε的高分辨率。
致谢
作者要感谢K. Omichi和R. Nomura(Fujikura Ltd.)制造了PM-FBG-FPI。
参考文献
[1] K. T. V. Grattan and B. Meggitt,Optical Fiber Sensor Technology: Advanced Applications-Bragg Gratings and Distributed Sensors.NewYork,
NY, USA: Springer, 2000.
[2] Yin and Shizhuo,Fiber Optic Sensors, Second Edition (Optical Science
and Engineering). Boca Raton, FL, USA: CRC Press, 2012.
[3] J. M. Lacute; opez-Higuera,Handbook of Optical Fibre Sensing Technology.
New York, NY, USA: Wiley-Blackwell, 2002.
[4] H. Patrick, G. Williams, A. Kersey, J. Pedrazzani, and A. Vengsarkar,
“Hybrid fiber Bragg grating/long period fiber grating sensor for
strain/temperature discrimination,”IEEE Photon. Technol. Lett.,vol.8,
no. 9, pp. 1223–1225, Sep. 1996.
[5] W. Du, X. Tao, and H. Tam, “Fiber Bragg grating cavity sensor for simultaneous measurement of strain and temperature,” IEEE Photon. Technol.
Lett., vol. 11, no. 1, pp. 105–107, Jan. 1999.
[6] R. Aashia, K. V. Madhav, B. Srinivasan, and S. Asokan, “Straintemperature discrimination using a single fiber Bragg grating,”IEEE Photon. Technol. Lett., vol. 22, no. 11, pp. 778–780, Jun. 2010.
[7] C. M. Lawren


