
英语原文共 13 页
基于自调试MRAS方法通过空间谐波去耦和传感器缩放、偏移和正交校正提高位置传感器精度
Caleb W.Secrest,Jon S.Pointer,Michael R.Buehner(IEEE成员)和Robert D.Lorenz(IEEE生活研究员)
摘要—采用模型参考自适应系统(MRAS)技术对多个非理想传感器特性进行去耦,提高矢量位置测量的精度。所考虑的非理想传感器特性包括:信号比例误差(矢量分量上的振幅不平衡)、信号偏移、传感器矢量分量之间的不完全正交性(正交误差)以及叠加在基本传感器输出上的额外空间谐波。给出了仿真和实验结果,对所提出的基于MRAS的解耦方法进行了评价。这里介绍的方法可以应用于多种形式的基于矢量的位置测量和估计,例如使用磁阻传感器、正弦/余弦编码器、分解器或无传感器(无传感器)方法。这些方法可以实时实现,并且非常适合基于矢量的位置传感器的自调试,以提高传感器的精度。
索引—交流电机驱动、磁阻位置传感器、模型参考自适应系统(MRA)、位置测量、分解器、自感(无传感器)控制、传感器谐波、正弦/ 余弦编码器。
命名法
转子机械位置
,转子机械速度
理想的传感器矢量相角。
观察者估计位置错误。
转子物理惯性
运动观察器控制器获得。
模型参考自适应系统(MRAS)自适应控制器增益
X 传感器输出矢量的实部。
Y 传感器输出矢量的虚部。
传感器输出矢量。
传感器信号偏移项。
空间谐波数。
位置测量误差的分量。。
第h个传感器谐波的大小。
第h个传感器谐波的相位。
样本期。
复数。
估计的物理参数
一、引言
理想情况下,基于矢量的位置传感器输出两个正交信号,其中一个与传感器角度的正弦相关,另一个与传感器角度的余弦相关。这些信号一起产生一个旋转矢量,该矢量的相位与机轴的角位置相关。输出旋转矢量的位置传感器,如正弦/余弦编码器、分解器和磁阻位置传感器,广泛应用于机器运动控制应用中。在反电动势(EMF)和空间显著性跟踪中,利用机器的磁特性使机器成为基于矢量的位置传感器[1]。在[2]中,研究表明,即使是基于霍尔效应的位置测量和增量光学编码器的离散性质,也可以解释为包含显著空间谐波含量的旋转矢量。在实际应用中,基于矢量的位置传感器输出可能包含标度误差(幅度不平衡)、正交误差、信号偏移误差和附加空间谐波。这些误差可能是传感器结构本身(例如,使用基于霍尔效应的位置测量或增量光学编码器时的离散位置信息)、对称性的实际制造限制(例如,由齿/槽效应和离散绕组引起的分解器或机器中的电感谐波)或在信号调节和采样期间发生(例如放大器和/或数字偏移和缩放误差)。此外,这些误差可能随温度或年龄而随时间推移而漂移,如果不考虑这些非理想的传感器特性,则会产生严重依赖于SPA的测量误差[3]。
有多种方法可以减少传感器引起的测量误差。有些方法依靠椭圆在传感器输出向量旋转时对图像进行最小二乘拟合[4]-[6]。另一种方法将传感器矢量分解为正序和负序分量,以提取基本上没有偏移、振幅和正交误差的矢量[7]。在[8]中,利用永磁同步电机(PMSM)的D轴电流提取传感器的振幅和正交信息。在[9]中,提出了基于三角分析的自适应抑制偏移、振幅和正交误差影响的方法。虽然[4]-[9]中的方法提高了传感器的精度,但这些方法忽略了传感器额外的空间谐波,使其不适用于谐波含量较大的传感器,或者在交流电机中存在多个空间谐波时,用于基于空间显著性跟踪的自感知[1]。在[10]中,内插和查找表用于校正锁相环(PLL)的参考模型,但未直接识别误差源,且PLL具有固有的滞后特性。
适当形成的矢量跟踪Luenberger类型的观测器提供速度和位置估计的零滞后滤波,并已被证明是圆弧切线计算的一种降噪替代方案,以及矢量跟踪状态滤波器(PLL)的零滞后替代方案[11]。以前的工作提出了一种矢量跟踪的解耦形式,即在交流电机中存在多个空间凸度时,采用Luenberger型观测器来改进基于自感知的转子位置估计[1]。交流电机中的多个空间凸起类似于外部位置传感器输出中存在额外的空间谐波。在[1]中,研究表明,除一个多个空间凸度以外的所有空间凸度的解耦都会提高转子位置估计精度和估计动力学[12]在使用极低分辨率霍尔效应位置传感时,利用[1]中提出的解耦技术来提高位置估计精度。在[1]和[12]中,谐波去耦不具有自适应性,因此不考虑运行期间传感器性能的变化。
本文研究了一种磁阻式位置传感器,提出了一种基于MRAS的自适应估计和解耦传感器信号偏移、标度和正交误差以及附加空间谐波分量的方法。使用[1]中提出的矢量跟踪观测器的去耦形式,将非理想传感器特性与传感器输出矢量去耦。基于MRAS的解耦的最终结果是提高了转子位置测量/估计精度。本文所提出的方法可应用于多种形式的矢量位置测量,如使用磁阻传感器、正弦/余弦编码器、旋转变压器或无传感器(无传感器)方法。这些方法可以实时实现,非常适合于基于矢量的位置传感器的自调试,以提高传感器的精度。介绍了磁共振成像结构的发展,并进行了仿真和实验评价。
- 模拟非传感器特性和导致位置估计误差
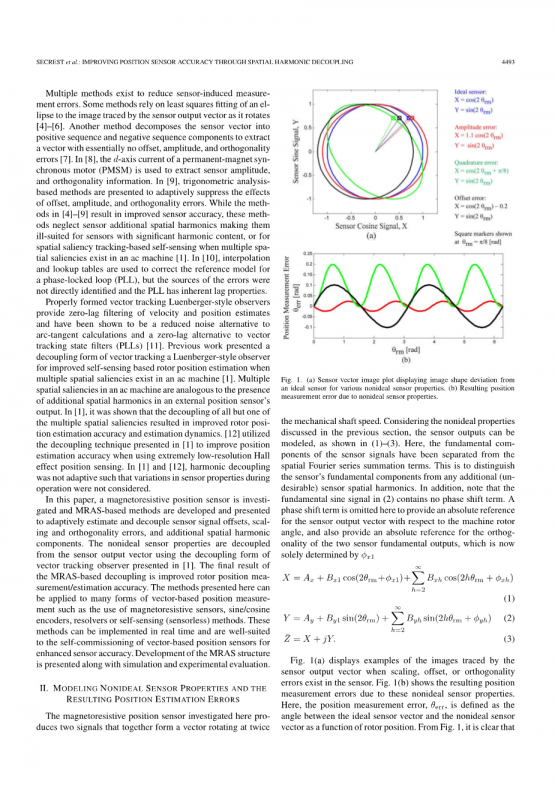
图 1 (a)传感器矢量图像图显示各种非理想传感器特性的理想传感器的图像形状偏差。(b)由于非理想传感器特性导致的位置测量误差。
这里研究的磁阻位置传感器产生两个信号,共同形成一个以两倍机械轴转速旋转的矢量。考虑到前一节讨论的非理想特性,传感器输出可以建模,如(1)-(3)所示。在这里,传感器信号的基本成分已经从空间傅立叶级数和项中分离出来。这是为了区分传感器的基本组件和任何其他(不需要的)传感器空间谐波。此外,请注意(2)中的基本正弦信号不包含相移项。这里省略了相移项,以提供传感器输出矢量相对于机器转子角度的绝对参考,并为两个传感器基本输出的正交性提供绝对参考,这两个传感器基本输出现在完全由决定。
图1(a)显示了当传感器中存在缩放,偏移或正交误差时传感器输出矢量跟踪的图像的示例。图1(b)显示了由于这些非理想的传感器特性导致的位置测量误差。在这里,位置测量误差err定义为理想传感器矢量和非理想传感器矢量之间的角度,作为转子位置的函数。从图1中可以清楚地看出对于所研究的传感器,信号偏移误差主要产生第二空
间谐波位置测量误差。此外,信号缩放和正交误差都会产生第四空间谐波位置测量误差。在[3]中,涵盖了由非理想传感器特性引起的位置测量误差背后的数学。
图 2(a)传感器矢量图像图,显示各种附加传感器空间谐波的图像形状;(b)由于额外的传感器空间谐波引起的位置测量误差。
图2(a)显示了当传感器输出中存在附加空间谐波时由传感器输出矢量跟踪的图像的示例。图2(b)显示了由于这些非理想传感器特性导致的位置测量误差。从图2中可以推断,由于第h个传感器空间谐波分量,位置测量误差的基本分量将会跟随(4)。同样,在[3]中介绍了由附加传感器空间谐波分量引起的位置测量误差背后的数学模型。
(4)
表I总结了这里讨论的传感器特性和基本空间谐波分量每个因素产生的系统位置测量误差。
图 3 Nonideal传感器属性缩放和解耦MRAS系统级框图。
图 4 一般MRAS框图[13]。
图 5 (左)物理位置传感器模型(右)Luenberger式矢量跟踪运动观测器的解耦形式,包括基于MRAS的非理想传感器属性估计和解耦结构及其输入/输出信号的放置。 MRAS组件以彩色显示。
- 基于MRAS的非理想传感器性能估计与解耦研究进展
一般的磁共振成像结构如[13]所示,如图3所示。在MRAS结构中,“参考模型”表示理想的实际过程行为。MRAS结构计算实际物理过程输出和参考模型输出之间的误差。然后将产生的“模型参考误差”(MRE)乘以实际过程的输入(或输入函数)。该乘法的目的是提取与特定已知的实际过程输入相一致的MRE组件。由此产生的“MRE的相干功率”(CPMRE)然后被传送到一个具有比例和积分项的自适应控制器。然后,自适应控制器的输出用于操作过程参数估计的缩放,或将有助于CPMRE的过程项解耦。MRAS结构的目标是驱动实际的流程行为与参考模型的行为相匹配,从而将CPMRE驱动为零。
- 基于MRR的非理想传感器特性解耦概念框图
图4将图3的重新表述为一个特定于非理想传感器特性去耦的图。物理磁阻位置传感器表示“实际过程”。注意,非理想特性的去耦发生在传感器的测量输出上,而不是实际过程的输入上。回到(1)和(2),对于正在调查的传感器,期望传感器输出产生以两倍机械速度旋转的单位矢量(即(hgt;1);)。该理想传感器模型将用作参考模型,将物理传感器输出(去耦后)与之进行比较。然后,将MRE计算为单位矢量参考模型与去耦后物理测量传感器输出之间的相位差。从表一可以看出,每一个非理想的传感器特性都会产生一个可预测的、系统的空间谐波位置测量误差。通过将MRE与这些已知的空间谐波位置测量误差函数相关联,可以提取出与每个特定非理想传感器特性相一致的MRE。产生的CPMRE信号将被发送到自适应控制器,其输出将使每一个非理想传感器特性解耦,从而对MRE起作用。该过程如图4所示。
- 矢量跟踪观测器的解耦形式
图5(左)物理位置传感器模型(右)Luenberger式矢量跟踪运动观测器的解耦形式,包括基于MRAS的非理想传感器属性估计和解耦结构及其输入/输出信号的放置。 MRAS组件以彩色显示。
在[1]中提出并使用的Luenberger型矢量跟踪运动观测器的解耦形式如图5所示。运动观测器的输入是传感器的测量输出,观测器的输出即是传递给电流调节器和运动控制器的位置反馈信号。图5也显示了MRAS结构相对于矢量跟踪运动观测器的位置。还显示了一些关键的MRAS结构组件和信号。其左侧是物理位置传感器的模型。传感器的输入是实际的转子轴位置,“传感器输出”是传感器产生的两个信号,这两个信号共同构成观察者跟踪的矢量。“传感器输出”包含“基本传感器输出信号”和“传感器缩放、偏移、正交性和附加空间谐波”分量的叠加。MRAS结构的目标是估计一个“缩放和去耦矢量”,该矢量与“传感器缩放、偏移、正交性和附加空间谐波”矢量相等或相反,这样当缩放和去耦矢量与被测传感器输出求和时,只剩下基本(理想)传感器输出分量。
MRAS结构的单位矢量参考模型已经作为运动观测器结构的一部分存在,并在图5中标记。参考模型的输入是估计的转子轴位置,输出是以两倍机械速度旋转的单位矢量。MRE可以从矢量跟踪观测器的矢量交叉积中提取出来。矢量交叉积的输出与去耦后的传感器输出矢量与单位矢量传感器模型之间的角度正弦成正比。在单位矢量传感器模型跟踪传感器输出矢量的情况下,两个矢量之间的角度将足够小,从而应用小角度假设,矢量交叉积的输出可以被视为近似等于两个矢量之间的角度。
MRAS结构的其余部分:MRE的相干功率计算、自适应控制器以及传感器缩放和去耦矢量的公式如图6所示,将在以下章节中讨论。
- 基于MARS的信号偏移校正和传感器二次谐波去耦
参考图1、2和表1,计算MRAS结构内的CPMRE所需的谐波函数是已知的。偏移误差和传感器的二次谐波(h=2)会产生与机器转子位置的二次空间谐波相关的位置测量误差。因此,与第二空间谐波旋转单位矢量(即与相关)相关的MRE可以通过将传感器偏移项(即传感器和项)去耦以及将与相关的传感器第二谐波项去耦来降低。实际上,对于偏移误差和传感器的二次谐波分量,不需要包括去耦项。通过只处理传感器信号的偏移项,传感器的二次谐波引起的位置测量误差也将被解耦。也就是说,通过将MRE与关联,并使用结果仅操
图 6 用于估计传感器信号偏移,幅度和正交性误差以及第h个空间谐波去耦的详细MRAS结构。
纵信号偏移项,可以将来自偏移误差和传感器二次谐波的净测量误差作为解耦量。
图6示出了信号偏移解耦矢量的MRAS公式。如前所述,MRE与第二空间谐波旋转单位矢量相关,并且得到的CPMRE通过具有增益K1和K2的自适应控制器。结果是一个偏移解耦矢量(),它将正确地解耦信号偏移误差和传感器的第二个空间谐波。另外注意,为了MRE的相干功率在自适应控制器内一致地累积,必须考虑机器旋转方向。图6显示了MRE与估计转子速度符号的乘积。
更好地理解信号偏移解耦矢量(即)如何同时解耦信号偏移误差和传感器的二次谐波分量,考虑仅包含这两个非理想特性的传感器。
注意,在适当的去耦之后,传感器输出的虚部Y除以传感器输出的实部X得必须等于被测角的正切。该陈述可以用数学表达,如(5)所示。(5)中的Xo和 Yo项表示从MRAS结构输出的信号偏移解耦矢量分量。鉴于(5)对于所有角度都必须为真(即0le;lt;2)并且可以选择角度并代入(5)求解之间的关系。这些关系如(6)和(7)所示
等式(6)和(7)表示信号偏移去耦矢量分量的闭合形式解,其将同时解耦信号偏移误差和传感器的二次谐波分量。请注意,这些封闭形式的解决方案仅为完整性而提供,并且MRAS结构自动收敛于正确的X0和Y0矢量分量,而无需实验或知道Ax,Ay,B2和。
图 7 传感器误差解耦矢量(品红色),当添加到测量的传感器输出(红色)时,产生理想的传感器相位关系(蓝色/点缀黑色)
图7显示了传感器偏移去耦矢量校正传感器偏移(参见图7(a))和去耦传感器二次谐波项(参见图7(b))的示例。请注意,图7显示了非理想的传感器属性,为了清晰起见,它们是独立地进行解耦的,但实际上,本文讨论的所有传感器错误都可以同时存在,并且仍然可以通过MRAS成功地进行解耦。然而,MRAS确实假定在正弦(y)和余弦(x)信号上,传感器谐
资料编号:[6021]
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


