
英语原文共 8 页,剩余内容已隐藏,支付完成后下载完整资料
Francesco DAgostino,Claudio Gennarelli,Rocco Guerriero,Giovanni Riccio,Catello Savarese
通过平面宽网格扫描获得的近场测量辐射功率的评估
UDK 621.396.677
IFAC 4.3.2
初步交流
本文设计了一个完整的程序,用来评估被测天线的辐射功率,通过创新的平面宽网格扫描收集的非冗余近场测量数据来实现。当天线在后半空间的辐射功率可忽略不计时,可用来评估天线的方向性。这种方法是利用了一个封闭式公式,根据远场球上辐射强度样本的数值计算其总辐射功率。这些数值是通过探针补偿近场-远场变换公式来确定的,用最优采样插值公式进行评估,通过数值模拟评估了该方法的有效性。
关键词:方向性评估、NF-FF变换、电磁场的非冗余采样表示、平面宽网格扫描
- 介绍
众所周知,发射系统的方向性函数描述了辐射强度的变化,这种强度是单位立体角的辐射功率,在空间中有方向性。因此,它的评估给出了关于天线容量的信息,来把辐射集中在一个给定的方向上。当使用专门的高性能通信链路和雷达系统的辐射结构时,这样做是很重要的。
根据其定义,方向性评价的关键点是总辐射功率的计算。它要求辐射强度达到在整个4pi;的固体角上的积分。然而,对于大多数实际天线,辐射强度函数的数学表达式(如果有的话)非常复杂,不能用解析方法进行积分。因此,利用现代计算设备的数值方法是很有必要的,比如在波长非常大的辐射系统中,当计算辐射强度很困难时,它们就会变得耗时。
文献中提供的大多数解决方案都是近似的,不适用于任何类型的受测天线(AUT)(参考文献[1,11]中的选定书目)。Dich在[12]中得到了一个由远场球上固定点的辐射强度,以此确定总辐射功率的公式。它是基于电磁(EM)场的球面波膨胀理论和[13]中的理论。它允许从模拟或测量数据方面进行方向性估计。[14]中提出了一个简单、快速、准确的采样插值(SI)公式。它与Dich的解决方案具有相同的优点,只需较少的数据量而不会失去准确性。该公式的推导基于发射天线辐射的电磁场的空间带限特性[15]和非冗余采样表示[16],采用辐射强度的采样扩展来减少求和的表面积分。这种公式只依赖于AUT的大小,因此为模拟或测量数据计算方向性提供了一种有效的方法。
如果不能以解析形式获得辐射模式,那么可以通过在AUT远场(FF)区域的球面上的测量来获得辐射模式。为了进行精确的天线测量,尽可能通过在消声室减少不可控环境条件带来的影响。然而,在处理电大天线时,由于无法满足远场FF的距离要求,只能进行近场(NF)测量,并且必须通过NF-FF转换技术恢复FF数据。其中,采用平面扫描的天线非常适合于辐射铅笔束图案的定向天线。实际上,对于笔形波束天线,后半空间的辐射功率(zlt;0)可以忽略不计,总辐射功率与前半空间的辐射功率基本一致。
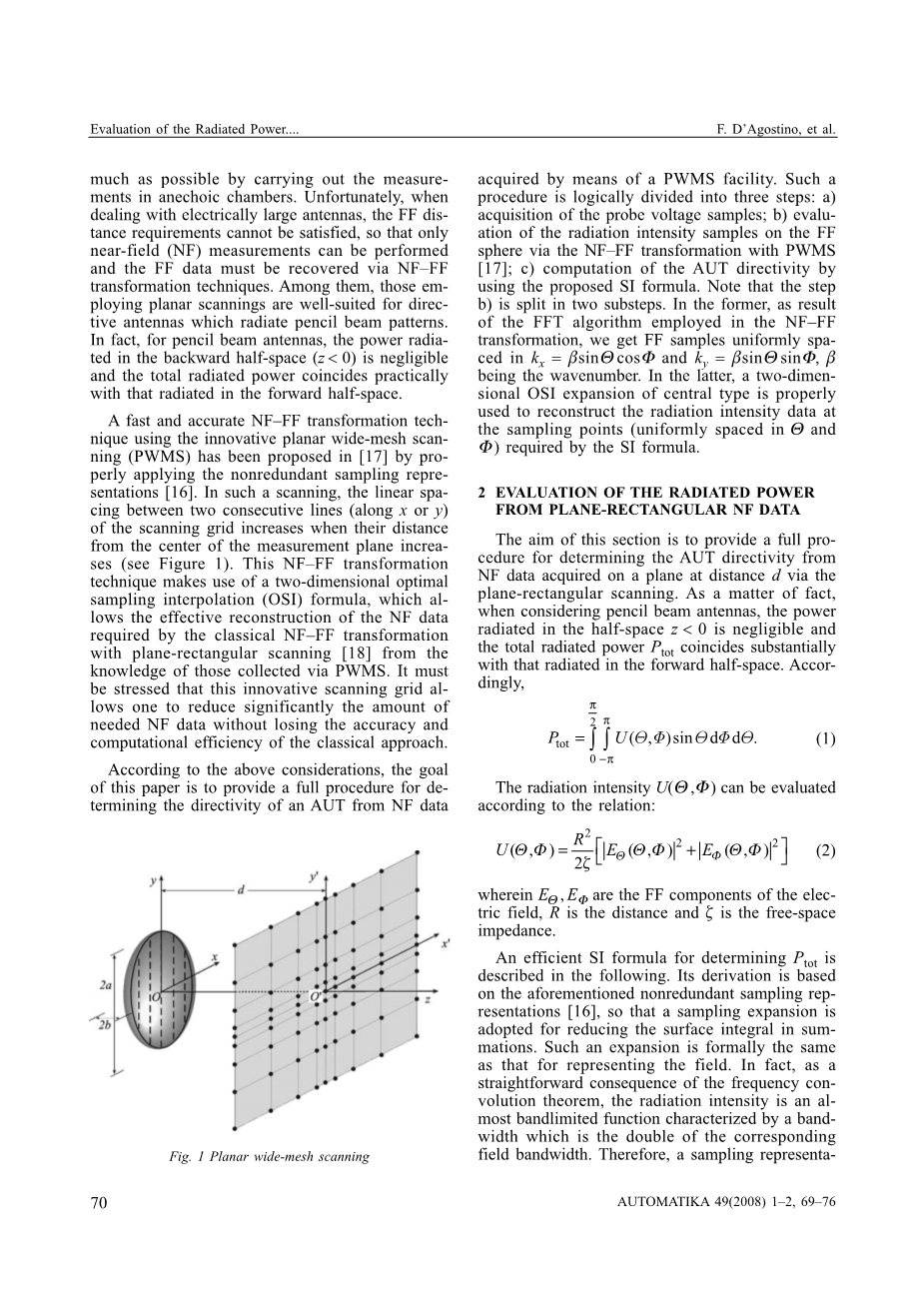
一种使用创新的平面宽网格扫描(PWMS)的快速准确的NF-FF变换技术,已在[17]中通过适当应用非冗余抽样表示提出[16]。在这种扫描中,扫描网格的两条连续线(沿x或y)之间的线性间距随着与测量平面中心的距离的增加而增加(见图1)。这种NF-FF转换技术是利用二维最佳采样插值(OSI)公式,通过PWMS收集到的信息,利用平面矩形扫描[18]有效地重建经典NF-FF转换所需的NF数据。必须强调的是,这种创新的扫描网格可以显著减少所需的NF数据量,而不会失去和经典方法类似的准确性和计算效率。
根据上述考虑,本文的目标是提供一个完整的程序,来确定AUT的方向性和从NF数据获得一个PWMS设施。这样的程序逻辑上分为三个步骤:a)采集探头电压样本;b)通过PWMS的NF-FF变换评估FF球面上的辐射强度样本[17];c)使用所提出的SI公式计算AUT方向性。请注意,步骤b)分为两个子步骤。在前一种方法中,通过对NF-FF进行快速傅立叶变换,我们得到了以kx=beta;sinTheta;cosPhi;和ky=beta;sinTheta;sinPhi;为单位的均匀分布的FF样本,beta;为波数。在后者中,适当地使用中心型的二维OSI扩展来重建SI公式所要求的采样点(均匀间隔为Theta;和Phi;)的辐射强度数据。
图1 规划广域梅斯扫描
- 平面矩形NF数据辐射功率的评估
本章的目的是提供一个完整的程序,通过平面矩形扫描在距离d的平面上获取NF数据来确定AUT方向性。事实上,在考虑笔形波束天线时,半空间zlt;0的辐射功率可以忽略不计,总辐射功率Ptot与前半空间的辐射功率基本一致。因此,
辐射强度U(Theta;,Phi;)可根据以下关系进行计算:
其中,ETheta;,EPhi;为电场的FF分量,R为距离,zeta;为自由空间阻抗。
下面描述了一个用于确定Ptot的有效SI公式。其推导基于上述非冗余采样表示[16],通过采用采样展开来减少求和中的表面积分。这种展开形式与表示场的展开形式相同。事实上,由于频率卷积定理,辐射强度是一个近似带限函数,其特征是带宽是相应场带宽的两倍。因此,只要采样间隔减半,仍然可以使用采样表示法。
根据[16]中的理论结果,我们将AUT看作是封闭在小凸面sum;中的,因为该凸面有旋转对称性,引入”还原电场”这一概念:
其中相位函数y(xi;)和观测面上曲线的最佳参数xi;必须确定。当用带限函数近似F,空间带宽超过临界值Wxi;[16]时,相应的带限误差可以忽略不计。因此,选择一个等于chi;′Wxi;的带宽可以有效地控制这种误差,其中,对于电性较大的天线,chi;′略大于单位的放大因子。
在这种情况下,观测面是FF球面,可以用子午线和平行线来描述。根据上述结果[16],子午线上的样本数仅取决于sum;的最大尺寸2a,而平行线上的采样率与其位置和最大横向尺寸2rho;max of sum;有关,即:
——经络
——平行线
因此,可以适当地使用以下基数级数(CS)展开来表示辐射强度:
(6)
其中
(8)
(9)
Int[x]给出x的整数部分,DJ()是Dirichlet函数,则
为了保证相对theta;的带限误差常数,需要用(9)中的theta;改变放大带宽因子chi;*。
值得注意的是,在本文所考虑的铅笔束天线的情况下,rho;max=a和展开式(6)是[14]中的截短版本。通过将(6)代入(1)并颠倒积分和求和顺序,得出:
现在,考虑到
我们可以得到
其中
在一些简单的分析操作之后,对这种积分进行评估:
其中
当平面矩形扫描获得的NF数据通过恢复SI公式(13)的使用来辐射强度样品,如前所述,必须使用适当的OSI扩展来确定所需采样点的辐射强度数据。
为了方便读者阅读,下面介绍了平面矩形扫描[18]的标准探针补偿NF-FF变换的关键步骤。在这种扫描中,NF数据的样本间隔是
lambda;是波长。根据这种情况,AUT辐射场的FF分量ETheta;,Phi;(Theta;,Phi; )与以下有关:1)两组独立测量(第二组探针旋转90°)时,探针输出电压VV和VH的傅立叶变换IV和IH;2)FF分量Ersquo;Theta;V、Ersquo;Phi;V和Ersquo;Theta;H、Ersquo;Phi;H。当用作发射天线时,探头和旋转探头辐射的关系是:
其中
现在,通过平面矩形NF-FF变换中使用的FFT算法进行探针电压的傅立叶变换,因此,得到AUT远场组件已知在指定的kx和ky值
其中Nx和Ny是沿x和y的测量点数。
一个二维的OSI方案可以在给定的方向Theta;,Phi;上得到ETheta;,Phi;。其数学论证依赖于AUT远场与探头电压的傅立叶变换。因此,如果这些电压在|x|gt;Lx和|y|gt;Ly条件下可以忽略不计,根据奈奎斯特采样定理,I~V,H = IV,H e—jbeta;cosTheta;在由间距分隔的点的矩形格点上可以从其样本中重建。
因此,可以使用以下OSI扩展来重建IV,H,其值为kx和ky,对应于方向theta;,Phi;:
其中sinc(tau;)是sin(tau;)/tau;函数,2qtimes;2p是保留样品的数量,n0和m0是最接近输出点左侧的样品的指数,
NXNYgt;NxNy是NF数据的总数(综合了用于“零填充”的数据)。此外,
是Knab的采样窗口函数[19],其中tau;0=sDelta;tau;和mu;=1minus;1/chi;,chi;gt;1是允许在使用OSI算法时控制截断误差的过采样因子。注意沿kx插值时,tau;0=qDelta;kx和chi;=NX/Nx,而沿ky插值时,tau;0=pDelta;ky和chi;=NY/Ny。
第三章 从PWMS样本到平面矩形NF数据
当通过PWMS获取NF测量值时[17],前一节的结果可用于评估AUT的辐射功率。让我们考虑一个非定向探头扫描一个距离AUT中心d的平面,假设它是笛卡尔坐标系x,y的原点(见图1)。对于这种探头,电压与AUT辐射场的有效空间带宽相同。最后一个假设为准平面,通过选择与大半轴和小半轴等于A和B的最小扁椭球重合的曲面sum;(包围它),可以得到一个有效的源模型(图1)。因此,引入“降压”,V(xi;)作为被测电压比较方便。
如果观测曲线是一条径向线,作为x′(或y′)轴,通过采用观测点P(xi;)和sum;得到子午线平面间的交点曲线的椭圆长度,其结果为[16]:
式中,E(|)是第二类椭圆积分,是椭球偏心率,是椭圆坐标,r1,2是从P到焦点的距离,2f是焦距。
为了将二维插值方案分解为沿直线的一维OSI扩展,必须采用(27)给出的相同参数xi;(eta;)来描述所有平行于x′(y′)轴的直线。因此,它们上的样本间距与x′(y′)轴相同(见图1)。这对应于使用本地带宽恒定的参数。由于最后一个总是小于或等于Wxi;,因此不进一步说明。这样得到的网格在离开中心时越来越宽。对于相位函数gamma;,可以证明表达式(26)仍然有效。以下OSI扩展可用于插入降低的电压样本:
其中
是样品,指样品的指标是否最接近输出点,2qtimes;2p为留样数,且
此外,
是Tschebyscheff抽样函数[16],其中TM()是次数M=Mrsquo;rsquo;minus;Mrsquo;、以及x0=qDelta;xi;或pDelta;eta;的tschebyscheff多项式。
OSI公式(28)可用于测量平面任何点的电压,特别是在用平面矩形扫描进行经典探针补偿NF-FFf变换后所需的电压[18]。
第四章 数值试验
下面是两个数值试验,以评估所提出技术的有效性。前一个示例是指半径等于15.6lambda;的均匀平面圆形阵列(图1)。它的元素,基本惠更斯源,沿y轴线性极化,径向和方位间距为0.6lambda;。测量平面距离AUT中心10lambda;,样品位于80lambda;times;80lambda;的正方形内,与防护样品分开。该阵列由一个长轴和短轴分别等于16lambda;和2lambda;的扁椭球体组成。探头选用工作在10GHz的开口波导WR-90矩形波导。值得注意的是,p=q=6和chi;=chi;′=1.20用于重建NF-FF变换所需的平面矩形NF数据[18]。重建的E平面图如图2所示。
图2 E面形(phi;= 90°);实线:精确;交叉:从PWMS数据重建
图3 FF的振幅分量ETheta;在Phi;= 60°;固线:精确;交叉:从PWMS数据重建
图4 FF的振幅分量EPhi;在Phi;= 45°;固线:精确;交叉:从PWMS数据重建
为了证明FF插值的有效性,图3和图4分别报告了Phi;=60°和Phi;=45°切割平面上的FF分量ETheta;的重建。可以看出,回收率非常准确。注意,在FF插值中假设p=q=6且chi;=512/250=2.048。
表1将(13)应用于NF-FF变换重建,归一化辐射强度最大值的FF数据,通过所产生的前半空间总辐射功率值与其他技术所得值进行了比较。如图所示,结果评估了程序的有效性。
表1
为了在更恶劣的条件下测试该技术的性能,可以改变阵列元件的激励以获得SLR=40dB的Tschebyscheff样。相应的结果如表2所示,在这种情况下,还应确认PWMS设施收集的NF数据进行测量,来确定AUT方向性的拟议程序的准确性。
表
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[20236],资料为PDF文档或Word文档,PDF文档可免费转换为Word


