贝尔格莱德冬季和夏季极端气温的日变化外文翻译资料

 2022-12-16 11:12

英语原文共 12 页，剩余内容已隐藏，支付完成后下载完整资料

贝尔格莱德冬季和夏季极端气温的日变化

M.Unkascaron;ević,I.Toscaron;ić

共11张图

2006年11月13日初稿，2007年10月27日刊登，2008年4月28日在线出版。

斯普林格2008

摘要

在此研究中，用广义极值分布和广义帕累托分布拟合贝尔格莱德冬季绝对最低气温和夏季绝对最高气温。研究人员发现这两种分布都是合理的。运用广义极值拟合冬季绝对最低气温时把趋势包含和北大西洋涛动指数作为位置参数变量，这显著改善了模型的变量纳入。运用广义极值分布和广义帕累托分布预计的100年反转水平和10年重现期在冬夏季节都是适用的。

１引言

人们越来越关注和重视极端气温及其变化的研究（伊斯特林等，2000；巩等，2004）。受极端事件的影响，经济损失以指数方式增长，人们生活中的损失成倍增加，这使人们注意到极端事件可能正在以一定频率增加。

自1861年以来全球地表平均温度开始上升。20世纪以来，全球气温以0.6plusmn;0.2℃的幅度增长（IPCC2001）。这种增长和最高气温的上升是紧密联系的（伊斯特林和霍尔顿1997）。

尽管对于近期气候的极端值和变异趋势的评定是有争议的，但温特斯韦克等（1996）的研究表明：普遍升温更易于导致夏季极端高温事件的增多和冬季极端低温事件的减少（例如，一些地区的霜日）。

极值原理的广泛使用为假设极端事件频率（最大或最小）遵循3种分布类型（网贝尔，弗雷歇或威布尔分布）之一的渐进定理提供了理由。把一个家族分布的单一描述称为广义极值分布（科尔斯2001；里斯和托马斯2001；Beirlant等2004）。

若日常资料可以获得，广义帕累托分布可以推广使用。广义帕累托分布较广义极值法是有优势的，因为它不但可以更好适应重尾分布而且可以考虑到更多的极端事件，但广义帕累托分布法在分析中就选择临界值和考虑可能的相关极值而言有两个缺点。即，那些与时间相关的事件。通常，把数据应用于一个分块的过程来解决这个问题。广义帕累托分布不仅可以用于分析气象学和水文学中的极值事件而且可以用于分析这些事件导致的灾害。（卡茨等2002；史密斯2003；博尔迪等2007）。

本研究既分析了贝尔格莱德1888-2003年间的冬季绝对最低温度和夏季绝对最高温度也分析了贝尔格莱德1936-2003年间冬季日最低温和夏季日最高温。尽管观察报告从1888年开始，但研究人员对于1936-2003年间最可靠的日常数据也进行了详细检查。为了检验这些分析，极端事件R程序包被使用，因为它开放性的资料，尤其是它不仅能很好地适应天气和气候应用，并且有在参数中纳入协变量的可能性。

本文的结构如下：第2部分是研究中的资料描述，第3部分是一些极值分布，第4部分是广义极值分布和广义帕累托分布对极端温度的适应性，第5部分是结论。

2资料

本文采用的是市中心公园贝尔格莱德气象台的资料。贝尔格莱德属大陆性气候区：日最低气温在1或2月份，日最高气温在7或8月份。此站的海拔高度在131.6米以上，地理坐标为 Psi;=44°48′N，lambda;=20°28′E。绝对最低和最高温度是用施耐德温度计测量的。这些测量技术和关键技术是由国家气象服务局控制的。在研究期间无站点的移动，资料组也未丢失任何记录。按照亚历山大德森的测试（1995）温度级数是齐次的。

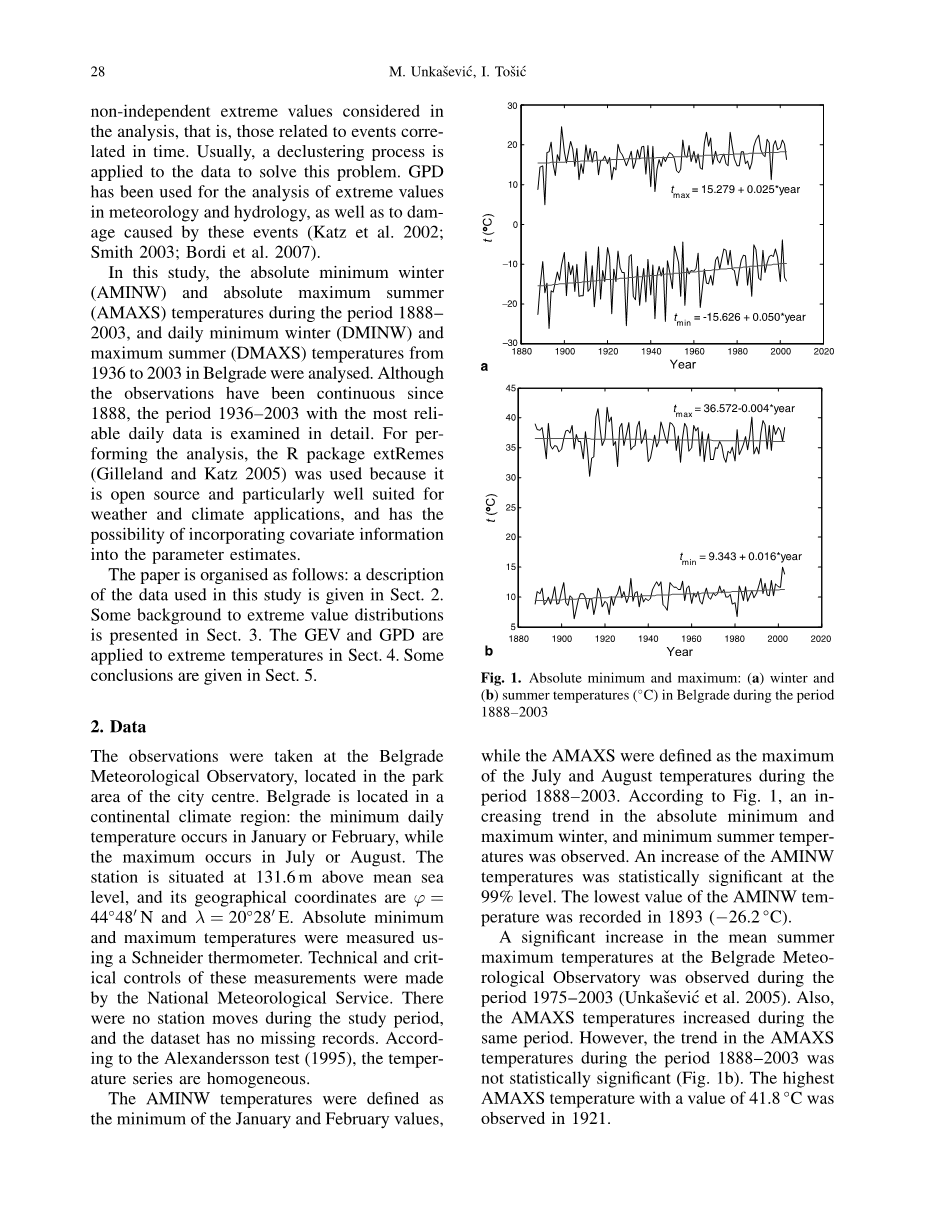
图1.贝尔格莱德1888-2003年间绝对最低和最高气温（℃）:（a）冬季和（b）夏季气温.

在1888-2003年期间冬季绝对最低气温是以1月和2月气温的最低气温定义的，而夏季绝对最高气温是以7月和8月气温的最高温度定义的。图1观测的是冬季绝对最低气温和夏季绝对最高气温的增长趋势。冬季绝对最低气温的增长在统计学上有99％的显著性水平。冬季绝对最低气温值（-26.2℃）是在1893年观测到的。

研究人员观测到在1975-2003年这一时期贝尔格莱德气象台的夏季平均最高温显著上升。（Unkascaron;ević等，2005）然而，1888-2003年间夏季绝对最高温的变化趋势在统计学上并不显著（图1.b）。在1921年观测到了夏季绝对最高温为41.8℃。

严等(2002)的研究表明，单站的结果在大范围内是具有代表性的，这意味着单站极值的研究结果也是大范围地区极值变化的结果。

3数据分析

3.1广义极值分布

广义极值分布来源于极值的特性描述。令x1,x2,hellip;为一个具有共同分布函数的独立变量序列，并令Mn=max(x1,x2,hellip;xn)。线性化后Mn的分布由广义极值分布序列中的公式按下面形式给出：

（1）

定义,

其中-infin;＜mu;＜infin;，－infin;＜xi;＜infin;。mu;，sigma;，xi;分别为位置，范围，形状参量。极值类型由xi;决定。xi;﹤0时为威布尔分布，xi;=0时为网贝尔分布，xi;﹥0时为弗雷歇分布。xi;值在确定尾部反应时是显性的；xi;﹤0符合最大值分布，xi;﹥0符合重尾增长分布。

等式（1）假设数据是时间段中的最小或最大值。mu;，sigma;和xi;的估计值由最大似然函数得到，（1）中的独立块极限z1,hellip;zn为：

在确定极端事件的反转水平时考虑随机变量的极值是很有意义的。反转水平Zp的定义以超过平均1/p年为标准（p是极端事件发生的频率）。对于（1）中给出的广义极值分布，反转水平由下面等式给出：

其中yp=-㏒(1-p)。delta法中变量

其中V是估计参量（mu;，sigma;，xi;）和

的协方差矩阵。

为了得到形状变量的似然函数,令xi;=xi;0并且把剩余参量mu;，sigma;的可能性增加到最大限度。（科尔斯2001）为得到近似置信区间，仍旧用xi;作为对数似然函数相应的最大值。

我们可以任意规定反转水平得到置信区间，这就要求对广义极值分布模型再参数化，以使ｚｐ成为考虑到剩余参量的最大化而得到对数似然函数模型参数中的一个值。

3.2广义帕累托分布

我们很自然地认为xi超过某些上界u时就会发生极端事件。对于足够大的u，X-u分布函数是由

近似确定的，设，,其中

(5)式确定的分布组被称为广义帕累托分布组。广义帕累托分布的尺度参数临界值（u﹥u0）的表示遵循（6）式sigma;u=sigma;u0 xi;（u-u0）。所以xi;ne;0时尺度参数是变化的，改进的尺度是由广义帕累托分布的尺度参数sigma;*=sigma;-xi;u，再参数化得到的，这个参数关于u是近衡量。

假设参数delta;和xi;是符合广义帕累托分布模型的量，对于超过临界值u的参数用变量x表示。即，对于,有

其中，zeta;u= Pr{X﹥x}。因此，标准（超过每一个平均观测值m）的解决方案为

其中xm是m-观测值的反转水平。如果每年有ny个观测值,N表示年数，它遵从m=Ntimes;ny.因此，N年的反转水平由下式确定：

对参数和反转水平较好的估计来自于似然函数。对于反转水平再参数化是有必要的。从（9）式可以看出，它遵循下式：

用（5）式计算使得一元参数似然值是xi;为最大值时。作为的函数，这是对于m-观测值的反转水平的似然估计。

图2.适合贝尔格莱德冬季绝对最低温度的广义极值分布诊断图（负转换）

4季节极端温度的分析

4.1广义极值分布的应用

贝尔格莱德冬、夏季极端气温资料由116个日最低、最高温度数据组成（也就是，成批的最小或最大值）。

图3.适合贝尔格莱德夏季绝对最高温度的广义极值分布诊断图（负转换）

图4.适合贝尔格莱德冬季绝对最低温度的广义极值分布对数似然的轮廓图（负转换）：（a）100年反转水平，（b）10年反转水平（c）轮廓参数。垂直虚线标记95％的置信区间。上界线表明对数似然轮廓的最大值， 对数似然轮廓值和95％的置信区间相交于最低点。

为了使广义极值分布适应于冬季绝对最低温度，最常用的方法是使min(x1,hellip;,xn)=-max(-x1,hellip;-xn),也就是，广义极值分布适应于这些资料的负值。

冬季绝对最低温度和夏季绝对最高温度的广义极值对数可能性的最大化使得估计值分别为（micro;，sigma;，xi;）=（-10.56,4.14，-0.07）和（micro;，sigma;，xi;）=（35.54,2.27，-0.30）。冬季绝对最低温度的标准误差为0.44,0.32,0.16，夏季绝对最高温度的标准误差为0.23,0.16,0.06。结合估值和标准误差，对冬季绝对最低温度而言mu;的近似95％的置信区间为（-11.43，-9.70），sigma;的为（3.50,4.77），xi;的为（-0.23,0.09）。对夏季绝对最高温度而言对每个参量近似95％的置信区间分别为（35.09），35.99），（1,95,2.59）和（-0.41，-0.19）。冬季绝对最低温度中xi;的负值（-0.07）比夏季绝对最高温度（-0.30）要小（绝对值）。根据xi;的负值可以得出结论：威布尔分布适应冬季绝对最低温度和夏季绝对最高温度，这就意味着最低、最高温度存在着极值。

图5.和图4表示的意义一样，只是此图表示的是夏季绝对最高温

适合贝尔格莱德冬季绝对最低温度和夏季绝对最高温度的广义极值分布模型精确度估计的多方面的诊断图分别为图2和图3。或然率和分位数表明合适模型的正确性：一组图上的点是近似线性的。作为参量xi;的一系列负值，反转水平曲线是非线性的。相应密度的估计和资料的直方图是一致的。资料的广义极值概率密度函数的优度检验方法是：卡方检验法和拟合优度检验法。冬季绝对最低温度（22.26﹤24.99）和夏季绝对最高温度（10.55﹤15.51）的条件是xn2le;xn20.05。四个诊断图都支持良好的广义极值分布模型。

4.11反转水平

计算冬季绝对最低温度和夏季绝对最高温度的反转水平是很有意义的。这些图是左下方的图2和图3（通过delta法估计的的95％的置信界限（等式3））。

delta法假设参数估计是匀称的，对于普轮廓参量并不总是这种情况。置信区间的较高精确度通常可以用100年的反转水平的似然函数得到。估计冬季绝对最低温度的反转水平为-26.8℃，有着95％的置信区间（-34.3，-23.5）。夏季绝对最高温度95％置信区间为（40.7,24.5）。冬季绝对最低温度和夏季绝对最高温度的10年反转水平为分别-19.2℃和39.3℃。（图4b和图5b）。图4C和图5C显示冬季绝对最低温度和夏季绝对最高温度xi;的的对数似然函数95％的置信区间分别为（-0.21,0.10）和（-0.39，-0.17）。这些图表明：（a）100年反转水平是非对称的，（b）10年反转水平是非对称的（c）形状参量是非对称的。由于对数似然性表示非对称性之间的差异，而且高标准的过程中数据提供了越来越弱的信息使得（a）和（b）之间上升的幅度有差异，且其程度的增加伴随着返回期的增长。

4.12协变量

北大西洋涛动与北半球冬季气温特殊模式和降水异常相联系(Vinther等2006)。根据Castro-Diacute;ez等（2002），欧洲南部的气温不仅对北大西洋涛动的位相敏感而且对北大西洋涛动活动中心的精确位置敏感。北大西洋涛动的影响（Hurrel 1995）是通过研究包含彭塔德尔加达和雷克雅未克间压力差的判断北大西洋涛动指数得到的。研究人员发现贝尔格莱德冬季绝对最低温度的增长和北大西洋涛动指数的相关系数为0.34（图6）。这个结论是通过模拟冬季绝对最低温度的更加复杂的合并协变量的极值模型的广义极值分布检验的。包含北大西洋涛动指数的位置参数（mu;）的广义极值分布如下：

其中mu;0（-14.13）和mu;1（0.76）由最大似然法确定。参数mu;1和冬季绝对最低温度的年增长率一致。在这种非平稳情况下，分布假设需要一些修改。一般而言，它是采用标准化的数据。拟合模型的残差概率图的表示在图7a。

图6.贝尔格莱德1888-2003年间冬季绝对最低气温与冬季北大西洋涛动指数的平均值。

进行测试以确定这个模型与北大西洋涛动指数作为协变量是对过去没有协变量的改进。更具体地，测试比较的可能性比，2log（l1/l0），l0和l1是两种模型的或然率，对chi;upsilon;2的分位数，其中，是估计参数的数目差异。在这种情况下，可能性比大概为5.10，表明这种模型比无协变量的模型有很大的改善。

由图1可以看出，在冬季绝对最低温度的位置参数中将趋势作为协变量是合理的，形式为：

或然率比的统计学测试是11.68，这是大于6.63chi;12分布的99％分位数。在图1中等式（12）的趋势与冬季绝对最低温度一致。sigma;（t）=exp(beta;0 beta;1t), sigma;（t）=(beta;

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[30603]，资料为PDF文档或Word文档，PDF文档可免费转换为Word

原文和译文剩余内容已隐藏，您需要先支付 30元 才能查看原文和译文全部内容！立即支付

以上是毕业论文外文翻译，课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。

您可能感兴趣的文章