
英语原文共 11 页,剩余内容已隐藏,支付完成后下载完整资料
基础退化的海洋导管架平台在循环荷载作用下的动力响应
摘要
采用1/10的比例模型研究了基础退化对海洋导管架平台动力响应的影响。对不同水深下的多层饱和土进行了试验研究。采用振幅和频率可调的激振器模拟实际载荷。根据人为质量相似原理和Buckingham pi;定理,利用量纲分析进行了模型缩比。研究了不同循环荷载作用下基础退化的水平动力响应。在ABAQUS中采用集总参数法或等效桩技术设计了有限元模型来处理桩-土相互作用,分析了导管架平台的动力特性。试验结果表明,基础退化与桩的运动幅值和频率有关。这种退化会导致导管架的固有频率降低,但对系统阻尼的影响很小。数值计算和试验结果的对比表明,采用集总参数模型和考虑p-y曲线的PSI单元来模拟土-桩-上部结构相互作用的精度远远高于采用等效桩技术。实验结果与理论计算结果基本一致。
关键词:海洋导管架平台,动力响应,循环荷载,基础退化试验,有限元法
- 引言
自20世纪40年代以来,海上建筑行业一直蓬勃发展。由于必须建造这些结构的水深不断增加,有必要使用新的模拟方法来了解这些结构在实际荷载作用下的行为(Wisch, 1998; Adrezin等,1996)。海上导管架平台不仅要承受来自自身和上部结构的巨大垂直荷载,而且还要持续承受来自风、浪、流、冰、地震以及它们的组合的水平循环荷载。支撑在桩上的海上导管架平台在海洋环境荷载下的动力响应受到地基特性的显著影响(Asgarian和Lesani, 2009; Mostafa和El Naggar, 2004)。许多学者研究了海上导管架结构的动力响应。Gudmestad和Moe(1996)在比较了API和北海设计实践方法后,推荐了一种统一的方法来选择用于计算水动力载荷的系数的合适的值,并进行全尺度实验来验证这些值。Sunder和Connor(1981)采用数值方法,考虑了波浪高度、波浪周期、水动力系数CM和Co的选择、甲板质量和迟滞结构阻尼的变化等因素,对导管架平台进行了灵敏度分析。在他们的计算中采用了等效的简化杆件模型。一些研究者使用模态分析在时域内计算海洋结构物的固有频率和振型(Karunakaran等,1997)或使用精确的Timoshenko管单元在频域内确定海上平台的动态响应(Horr和Safi, 2003)。Ou等人(2007)开发了一种阻尼隔振系统来控制钢导管架海洋平台的振动。把阻尼隔振系统安装在结构的1/10的比例模型上,并在模拟冰荷载和地震荷载的振动台上进行了试验。他们进行了数值模拟,并将模拟结果与实验结果进行了比较,模拟结果与实验结果吻合较好。Elshafey等人(2009)从理论和实验上设计了一个缩比模型来研究海上导管架平台在随机波浪荷载作用下的动力响应。在空气中和拖曳池中进行了试验。实验结果与理论计算结果完全一致。
支承导管架平台的桩体在土体中循环移动,从而增大土体的超孔隙压力,削弱地基,降低侧向土阻力。关于桩-土相互作用和地基退化的研究文献较少。Matlock(1970)和Reese等人(1974)研究了软粘土、硬粘土和砂土在循环荷载作用下的静阻力衰减规律。他们所提出的静力土抗力公式被API标准(API, 2000)采用。此外,Novak等(1978)、Nogami和Novak(1980)、Nogami和Konagai(1988)、El Naggar和Novak(1996)、以及El Naggar和Bentley(2000)研究了粘土或砂土的动阻力,并分析了振动荷载下桩的动力反应。Mostafa和El Naggar(2004)用有限元法研究了群桩支撑的固定式海洋平台的响应。他们分析了土壤特性和桩-土相互作用对群桩支撑的导管架结构的动力特性的影响,他们的结论是结构的动力特性受到土壤特性和桩-土相互作用的显著影响。Wang和Feng(2005)利用振动台上的模型试验研究了液化沙和桩的相互作用。CCS(1992)规定了等效桩技术,以从泥线以下桩直径的6-8倍处的点固定桩的下部的方式来简单处理桩-土相互作用。在相对较长时间循环荷载作用下,计算的海洋导管架平台的固有频率与实际值有明显的差异,因为该方法没有充分全面考虑桩-土相互作用以及基础退化对平台动力响应的影响,尽管该方法可用于快速估计近海结构物的行为(Shang等,2008)。
本文设计了一个包括有上部结构的缩比模型、桩和土的实验系统,研究了地基退化对海上导管架平台的动力横向特性的影响。研究了在不同循环荷载作用下地基退化情况下平台的水平动力响应。利用土压力传感器和孔隙水压力计分别估算地基反力和土孔隙压力。实验结果与ABAQUS中用集总参数法或等效桩法设计的有限元模型的结果进行了比较,验证了有限元模型的正确性。对于海上结构动力特性的研究,特别是在循环荷载作用下地基退化的情况下,有限元模型可以以一种实用和廉价的方式进行大量的模拟。
- 实验装置
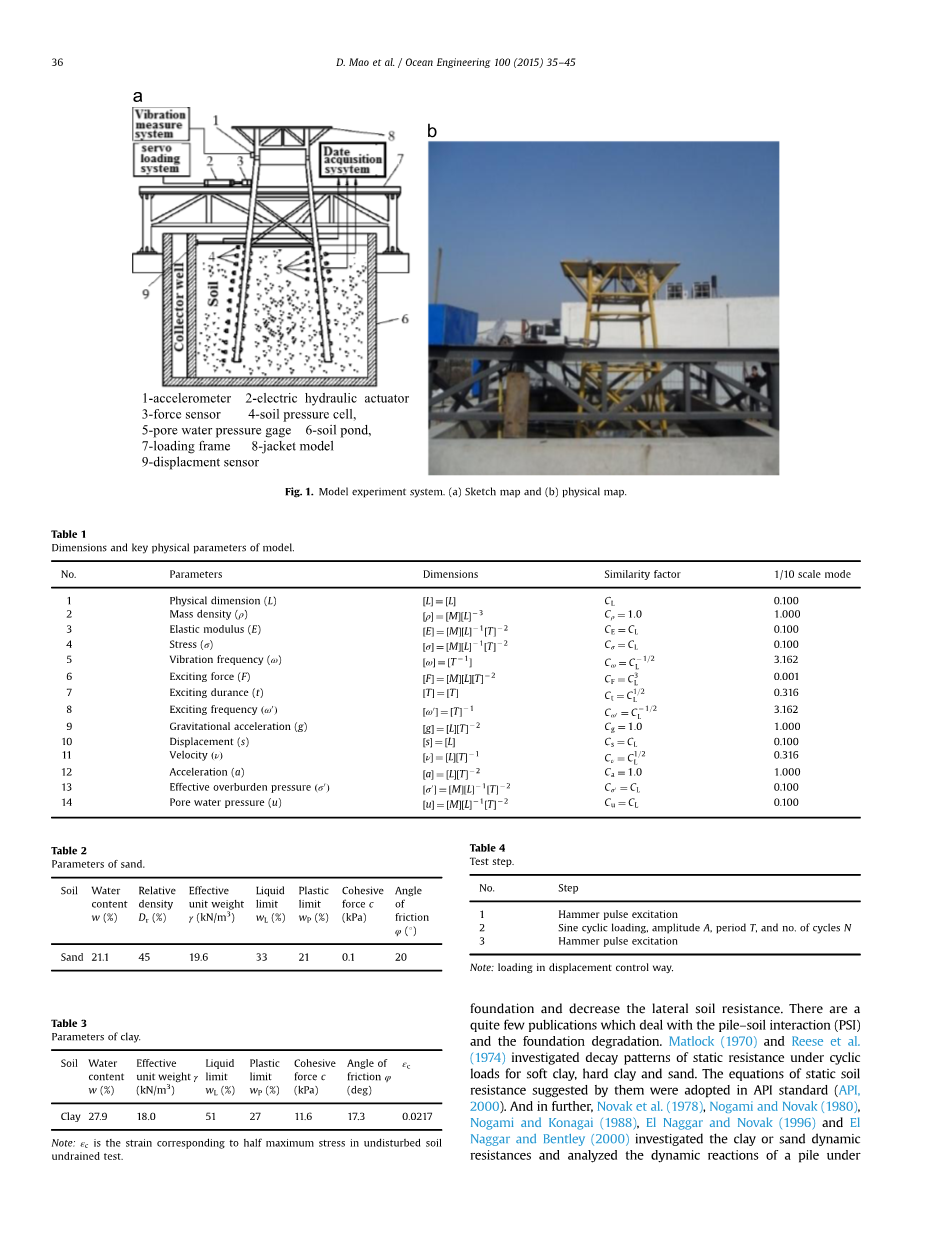
已开发的实验系统如图1所示。它由导管架-桩-土系统、电伺服加载系统、传感器和数据采集系统三部分组成。
图1 模型实验系统.(a)示意图和(b)真实图
2.1导管架-桩-土系统
导管架-桩-土系统包括原型结构、缩比桩和填充分层土壤的钢筋混凝土土池。根据现有的海上导管架平台JZ20-2MUQ,原型结构是一个具有斜支撑和X支撑组合的四腿导管架。模型导管架和模型桩由Q235钢制成,弹性模量是200 GPa,泊松比是0.3。在尺度工程模型试验中,人工质量相似定律和基于白金汉pi;定理的忽略重力的相似原理被广泛应用于补偿当重力相似系数为1时的重力效应和惯性效应(使结构的刚度保持不变)(Ling等人,2004)。如以下方程式所示,应在原型结构上添加人工质量(Ling等人,2004)。
其中m0为人工质量,mp为结构的初始质量,mm为原型结构的质量。为模型的总质量,因为质量相似系数为,cL为长度相似系数。由于选择了长度、时间和质量作为基本尺寸,因此模型的尺寸和关键物理参数如表1所示(Li等人,2012)。模型导管架总高度为6米。桩是用外径90mm、厚3mm、长3m的管建造的,结构总重量为511kg。对于土池,其长度*宽度*高度为5.0 m*5.0 m*3.5 m。池内自上而下的分层土壤分别为厚度为1 m的粘土、砂和粘土。实验用的土壤在多次回填和注水后天然加固4个月以上。土壤参数通过土壤试验获得,如表2和表3所示。
表1:模型的尺寸和关键物理参数。
表2:砂的参数
表3:粘土的参数
2.2电动伺服加载系统
建立了以电液伺服执行机构、驱动控制器、计算机和控制软件为主组成的高精度电液伺服加载系统,对海洋环境载荷进行仿真。液压油缸的行程、最大速度和最大载荷分别为0.35m、0.2m/s和50kn。控制器结合力传感器和位移传感器可以控制液压油缸的位移和力的大小。通过在计算机上安装的加载程序,可以进行频率为0Hz~5Hz的各种循环加载和脉冲加载。
2.3传感器布置及数据采集系统
如图1(a)所示,在桩上安装了15组半桥式测量应变计,15个微型土压力传感器沿20cm的间隔纵向均匀地布置在非常靠近桩的土中。采用应变计测量桩的弯矩。采用微型土压力传感器直接测试土壤阻力,得到不同深度的p-y曲线。将微型孔隙水压力计按加载方向放置在桩前后的土中。在模型导管架上部的两个水平方向上,在每个主管接头处安装两个加速计。在泥线位置将位移传感器连接到桩上,测量该处的位移。记录36个主管接头的脉冲响应,利用MaCras软件的频率响应分析模块可以给出固有频率。
2.4加载
将正弦循环位移荷载施加在一个焊接在模型导管架上的加载框架上,其位置在泥线(冰荷载区)以上1.8 m处。位移加载幅值A在50mm ~ 200mm范围内,步长为50mm,每个幅值可以分别匹配不同的周期例如10.0 s、5.0 s、2.0 s、1.0 s和0.5 s。循环数目N是200。循环加载前和循环加载后分别施加脉冲激励,记录响应曲线,通过比较二者的变化,分析土壤退化的影响。表4说明了测试步骤的一个循环。在试验中,保持脉冲激励的大小为常数是非常重要的。
表4:测试步骤
- 有限元模型
模型导管架平台的动力响应用二阶矩阵微分方程描述如下:
式中M是质量矩阵,C是阻尼矩阵,K是刚度矩阵,和分别是加速度、速度和位移矢量,f(t)是激励力。
使用ABAQUS软件求解方程(2)。采用梁单元对缩比导管架的主要构件进行建模(图2)。一般情况下,由于土体不仅具有粘性阻尼,而且具有辐射阻尼,所以对于桩-土相互作用问题土体刚度是高度非线性的。处理桩-土相互作用有三种方法:集总参数模型、等效桩技术和接触单元法(Dongfeng等,2015)。本文采用前两种方法。
图2:导管架-桩-土有限元模型
3.1等效桩技术
根据CCS(1992),在计算中假定阻尼矩阵和刚度矩阵为线性的,将等效桩的下部固定在刚性基础上。等效桩的长度是通过使等效桩的刚度特性与桩-土体系相同的方法确定的。等效桩下端在泥线以下约6-8倍的桩径处固定。本文采用6倍的桩径。
3.2集总参数模型
集中参数模型实质上是用等效质量-弹簧-阻尼系统来代替地基动力刚度。用一系列离散的质点或离散的连续梁来模拟缩比桩。将远离结构的基础简化为半无限大刚体。本文采用离散的连续梁。由于忽略了土体的剪切作用,采用Winkler模型对等效土体进行模拟,因此它可以通过施加非线性弹簧来处理层状和非线性土体。这里在ABAQUS中通过输入包括线性和非线性部分的lsquo;PIPE-SOIL STIFFNESSrsquo;的关键参数,采用不同深度的p-y曲线来定义形成PSI单元的管-土本构关系。对于四根桩,沿加载方向共设置76个PSI单元,如图2所示。图3展示了由与缩比导管架桩相同的材料和相同的尺寸制成的单个模型桩,在同一土壤池中对缩比导管架桩进行测试以获得静力p-y曲线。利用三组试验桩弯矩数据的平均值进行六阶多项式拟合(Wang和Feng, 2005)得到的饱和土p-y曲线如图4所示。
3.3数值模拟试验
为了将仿真结果与实验结果进行比较,采用线性扰动步长进行振动模态和频率提取。数值模拟中使用的载荷应与实验中的载荷相同。采用CCS等效桩法计算了前20阶模态。如图5所示,前三阶模态分别是绕x轴和y轴的弯曲和绕z轴的扭转。需要注意的是,x方向与模型的长边平行,y方向与短边平行,z轴垂直于xy平面。
图5:前三阶模态。(a)第一阶模态为绕x轴的弯曲;(b)第二阶模态为绕y轴的弯曲;(c)第三阶模态为绕z轴的扭转
- 实验结果
4.1单个模型桩的弯矩
采用p–y曲线PSI单元计算了单桩的弯矩分布,并在三种不同的加载下进行了试验。结果如图6所示。数值计算结果与实验结果吻合很好,说明本文所采用的包含p–y曲线PSI单元的有限元方法是正确的。
图6:弯矩的比较
4.2模型导管架的固有频率
得到了原型导管架在不同水深下的固有频率和振型,前三阶固有频率如表5所示。试验结果表明,水深对海上结构的固有频率影响不大。
数值模拟结果与实验结果的比较如表6所示。采用p–y曲线PSI单元的数值模拟结果与试验结果的相对误差在5.2% ~ 7.8%之间,而采用等桩法的数值模拟结果与试验结果的相对误差在22% ~ 29%之间。
显然,采用集总参数模型和p–y曲线PSI单元的有限元模型比采用等效桩法的有限元模型具有更高的精度。集总参数法的仿真结果与试验结果吻合较好。采用p–y曲线 PSI单元计算得到的固有频率略大于实验值。簇桩效应可能会导致一定的差异。如果在p–y曲线中考虑簇桩效应,上述差异将较小。
表5:不同水深下模型导管架的前三阶固有频率和振型
表6:前三阶数值模拟结果和试验结果(水深为0米)
4.3循环荷载作用下地基侧阻力衰减规律
随着循环次数的增加,桩周土体的超孔隙水压力增大,特别是当加载频率较高时,超孔隙水压力明显增大,如图7所示。超孔隙水压力的增大是影响土体阻力的一个重要因素因为它会减小土体抗剪强度和承载力 (Mostafa和El Naggar, 2004)。
根据梁的变形和应力分析理论,模型桩的侧向位移和侧向土阻力可由测量的桩应变求得(Matlock,1970)。图8为循环过程中模型桩的侧向位移分布。拐点随桩头位移的增大而下移,变形桩的全长变长。通过对不同循环荷载前后桩侧土阻力分布的比较(图9),最大土壤阻力出现在泥线以下0.2 m处,衰减主要发生在泥线以下不超过1 m深的顶部粘土层。图10显示了不同循环荷载作用下泥线以下0.2 m处p-y曲线的变化。循环荷载越大,土壤阻力衰减越大。在前10个循环中,土壤阻力衰减非常严重,在100个循环内趋于稳定,这与萨宾和奥斯汀湖的Matlock现场试验(Matlock,1970)一致。然而,当桩体位移达到0.02m(0.2D)时,在本试验中没有出现马特洛克所说的土壤阻力连续衰减的现象,但经过25次循环后趋于稳定。
图7:超孔隙压力的变化。(a)A=100mm,T=10s的循环荷载;(b)A=100mm,T=0.5s的循环荷载
图8:桩的侧向位移分布
图9:循环荷载前后土壤阻力的比较
图10:泥线以下0.2m处土层的p-y曲线
在小幅值循环荷载作用下,不同加载频率引起的土阻力的变化较小。当循环荷载幅值较大时,高加载频率会导致土壤阻力增大。大幅值高频(2Hz)荷载作用下,尽管超孔隙水压力明显增大,土体抗剪强度降低,但由于桩速度的增加,阻尼也随之增大,最后,使土壤阻力大于低频荷载下的阻力。Reese(1974)和El Naggar和Novak(1996)详细研究了阻尼对土壤阻力的影响。
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[237765],资料为PDF文档或Word文档,PDF文档可免费转换为Word


