
英语原文共 6 页
外文翻译
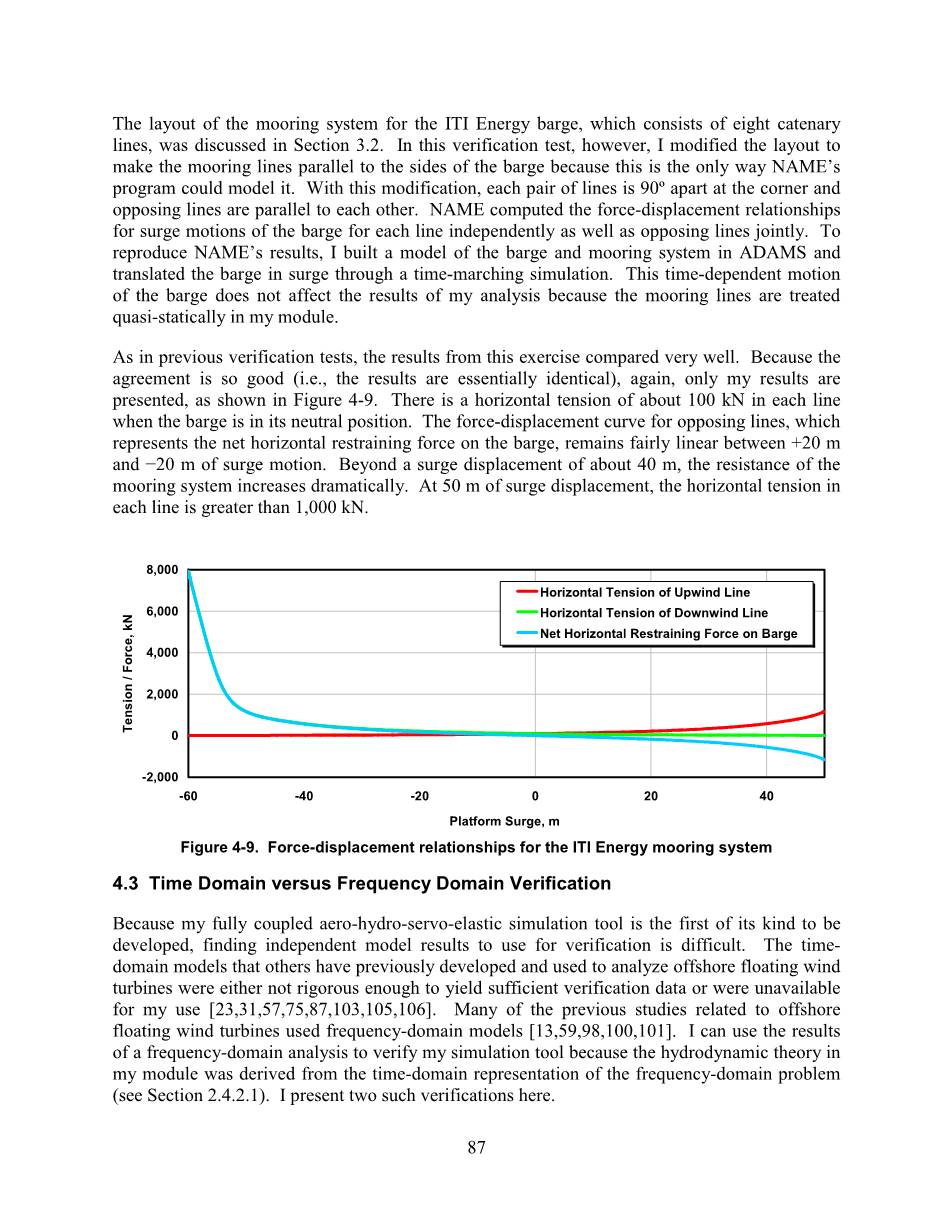
我们在3.2小节讨论的ITI Energy barge平台风机的系泊系统的布局,由8条系泊缆绳组成。在这个验证试验中,我修改了这个系泊系统的布局,使系泊缆绳与barge平台风机的边缘平行——这是NAME的程序能够模拟它的唯一方法。修改之后,在角落里的每一组线都相互垂直并且相对的线互相平行。NAME计算了在每条独立线路上的纵荡运动,以及在相反线路上的纵荡运动上力与位移的关系。为了复制NAME的结果,我在ADAMS中做了一个barge平台风机和系泊系统的模型,并且通过时间推进模拟翻译了barge平台风机的纵荡。barge平台风机的这种随时间变化的运动不会影响我的分析结果,因为系泊缆绳在我的模块中是准静态处理的。
与以前的验证测试一样,这次测试的结果进行了很好的比较。因为这个拟合的太棒了(结果基本相同)。同样的,这里只给出了我的结果,如图4-9所示。当barge平台风机处于中性位置时,每条线上的水平拉力约为100KN。相反的力-位移曲线线条,代表在barge平台风机上的网络横向约束力,相当于 20米,minus;20米之间的线性纵荡运动。当纵荡位移超过40米左右时,系泊系统的阻力急剧增大。当纵荡位移为50 m时,每条线的水平拉力均大于1000KN。
4.3关于时域和频域的验证
由于我的全耦合气动-水动-控制-弹性仿真工具是首创,很难找到独立的模型结果进行验证。其他人之前开发并用于分析海上浮动风力涡轮机的时域模型要么不够严格,无法产生足够的验证数据,要么无法供我使用[23,31,57,75,87,103,105,106]。以往有关海上浮动风力涡轮机的许多研究使用[13,59,98,100,101]的频率较高。我可以使用频域分析的结果来验证我的仿真工具,因为我模块中的水动力理论是由频域问题(详见2.4.2.1)的时域表示推导出来的。我在这里提出两个这样的验证。
频域解描述平台对以单一振幅、频率和方向传播的入射波的正弦稳态响应。如2.4.2.1节所述,频域问题的解一般是用响应幅值算子来表示的,响应幅值算子是支撑平台上每个自由度的运动的复值振幅,按每一单位的波幅来标准化。在时域模型中,通过引入规则周期波作为扰动函数,并在足够长的时间内进行仿真,以确保所有的瞬时行为都消失,可以得到浮台的正弦稳态响应。作为对我的完全耦合模型的第一次验证,我们使用这样的时间序列模拟来回收离散入射波频率下的响应幅值算子,并重复这个过程来找到每个期望频率下的响应幅值算子。在这个验证测试中,我们使用了关于MIT / NREL SDB的韦曼频域结果。
正如我在2.4.2.1节中所讨论的,由于频域表示不适用于瞬态分析,浮动平台在频域问题中对随机海况的响应只能进行统计表征。具体地说,线性化的浮体在受到波高程为高斯分布的海况激励时,其运动响应为高斯分布。运动响应的标准差由Wiener-Khinchine定理决定[85,101]。在时域模型中,运动响应的分布可以通过对一系列足够长的仿真结果进行后置处理来确定,从而保证结果的统计可靠性(这个过程可以重复,以找到每个期望的海洋状态的分布)。我们使用这个过程作为我的完全耦合时域模型的第二次验证,再次使用韦曼的[101]频域结果对MIT / NREL SDB进行比较。
在这些验证测试中,我们使用了第3.1节中描述的安装在第3.3节中描述的安装在MIT / NREL SDB上的NREL海上5兆瓦基线风力机。我选择了这个配置和韦曼的[101]频域结果,因为这是唯一的配置,也是唯一记录了足够信息的研究,足以让我建立一个系统模型,并比较所有六种平台运动模式的结果。
韦曼使用WAMIT计算了MIT / NREL SDB的频域水动力特性,并对3.3节中描述的扩展系泊系统进行了建模,仅在纵荡和横荡自由度下进行线性恢复。韦曼利用SML的LINES模块[50]求出4000 KN/m下的线性恢复系数。在韦曼的线性化系统模型中,通过将体质量矩阵与涡轮的质量特性相结合,将水动力阻尼和恢复矩阵与阻尼相结合,以及转子空气动力学和陀螺学的恢复贡献相结合,得到了风力机的特性。韦曼忽略了风力机的弹性,只考虑了barge平台风机的六种刚体自由度模式[101]
4.3.1对稳态响应的验证
为了进行比较,我构建了安装在MIT / NREL SDB上的NREL海上5兆瓦基线风力机的AeroDyn和HydroDyn模型。为了保证与韦曼模型的合理相似性,分离水动力和系泊系统的运作,我在没有任何控制系统(即(采用固定转子转速和固定叶片间距)或浮式支撑平台的六刚体自由度以外的任何运动方式下给涡轮机建了模。在环境条件下,采用恒定、未修改的风速为11.2 m/s风(如韦曼所采用)和有规律单位振幅的周期波(峰间值为2 m)。风和波浪都是同向的,并与纵荡坐标对齐。
当我们第一次尝试运行时域仿真时,我使用我的准静态系泊系统模块进行了扩展系泊系统的FAST建模。但我们很快发现,扩展系泊系统的非线性恢复使得响应永远无法达到正弦稳态状态,从而消除了任何响应幅值算子恢复的可能性。为了解决这个问题,我决定删除与我的系泊模块的接口,而不是像韦曼那样,用线性恢复系数(仅在纵荡、横荡和艏摇的情况下)对系泊系统建模。因此,下面给出的结果对于验证我的系泊系统模块的时域实现是没有用的。不过,它们对于验证我的流体动力学模块的时域实现仍然很有用。
利用线性化的系泊系统模型,我们进行了一系列2000秒的仿真,以给它们达到周期稳定状态的时间。即使经过这么长时间,平台的运动对于横荡、横摇和艏摇的响应仍然不是完美的正弦曲线。我们进行了10次模拟,将入射波的离散频率从0.15 rad/s均匀增加到1.05 rad/s。利用每个模拟的最后一个周期,我们计算了三个平移和三个旋转平台响应的振幅。因为入射波是单位振幅,所以这些响应幅值等于响应幅值算子的大小。对于旋转响应,我们通过平台半径(18 m)将响应幅值算子归一化,就像韦曼所做的那样[101]。我们将结果添加到韦曼生成的无量纲响应幅值算子图中。在这些测试中,我们没有对反应的阶段做出比较。
如图4-10所示,我们的时域预测与韦曼频域分析对平台纵荡和垂荡模式的预测非常相似。这让我相信我对平台流体动力学的时域实现是正确的。平台纵摇曲线似乎有相似的特征,但部分在大小和频率上都不同。另外三个参数横荡、横摇和艏摇的响应非常小,很难进行比较。因为这些模态的振荡在2000秒后还没有完全变成正弦,我们质疑这些比较是否有意义。尽管在这种结构中没有空气动力学或水动力学对平台艏摇模式的激励,但由于转子的转动惯量与平台的纵摇运动相结合,会产生陀螺艏摇力矩,所以艏摇响应是非零的。
我认为这种纵摇响应幅值算子的差异是由于我的模型与韦曼的在纵摇气动阻尼上的差异造成的。韦曼证明了平台纵摇阻尼完全由转子空气动力学控制,而不是波辐射(参见文献[101]附录A.1)。对于其他运动模式,如纵荡和垂荡,情况并非如此。在韦曼的分析中,barge平台风机纵摇的气动阻尼是恒定的(利用FAST和AeroDyn将转子气动推力沿平台平均纵摇方向线性化得到)。在我的模型中,随着涡轮的逆风和逆风摆动,barge平台风机桨距的气动阻尼也会发生变化。
4.3.2对随机响应的验证
为了验证随机响应,我针对安装在MIT / NREL SDB型风机上的NREL海上5兆瓦基线风力机建立了三个带有AeroDyn和HydroDyn模型的FAST模型。第一个与响应幅值算子的比较中使用的相同:它有一个刚性涡轮,没有控制系统,并且在纵荡和横荡时采用线性化的系泊系统。对于第二个模型,我将线性化的系泊线模型替换为FAST与准静态系泊系统模块之间的标准接口。为了验证这些简单的模型与高保真度模拟的一致性,在第三个模型中,我用一个足够灵活的模型替换了刚性涡轮,并启用了变速发电机扭矩和叶片间距控制系统。
关于韦曼频域研究的已发表结果[101]包括了各种海况、风速和水深下高斯分布响应的均值和标准差。我选择将这三种模型与其中一种进行比较。我选择的情况大致是额定风速(11.2 m/s),水深200米,波浪高程时间序列测试中考虑的相同波浪条件(见4.1.1节)。在前两种模型中,我们使用的是稳定的无修剪风。而在主动控制系统的第三种模型中,我们使用的是紊流和剪切风,平均轮毂高速度为11.2 m/s, IEC范畴B级紊流[33]。与以前一样,风和浪是同向的,并与纵荡坐标对齐。
对于每一个模型,我们计算了除了前30秒之外的所有输出的概率密度(即每个只差3个小时),它对随机波浪使用了不同的随机种子(如4.1.1节所示)。在计算概率密度之前,我们构造了这四种情况的集合。我们将得到的直方图与韦曼频域分析均值和标准差得到的正态概率密度函数进行了对比
图4-11给出了时域结果与韦曼频域结果的比较。由于我的第二个模型和第三个模型的结果之间的差异比转换到非线性系泊线带来的变化要小得多,所以图中只显示了第一个模型和第三个模型的结果。与响应幅值算子一样,我的模型与线性化的系泊线的纵荡和垂荡的预测非常吻合。在线性化系泊系统的仿真中,纵摇响应的传播比韦曼的预测要窄。这与图4-10所示的纵摇响应幅值算子对比一致,即韦曼的响应幅值算子在0.429 rad/s时大于我的模型预测的幅值。
将非线性系泊系统模块引入FAST仿真后,平均纵荡、纵摇和垂荡响应均显著降低(见图4-11)。这是因为一旦缆索绷紧,刚度就会急剧增加,而系泊系统实质上就像一个四杆机构。这就避免了平台上升到同样的高度,也避免其顺风行驶太远。转子上的推力试图使涡轮机在顺风时倾斜,但张紧度更高的逆风系泊线阻止barge平台风机的逆风端离水面太远;平台反过来又被轻微地推到逆风处。因为在高保真度模型中,系统中存在更多的耦合,所以横荡、横摇和艏摇的值的扩大也比简单模型中大得多。
第五章 载荷分析综述与描述
我进行了两组初步的负载分析。第一个是安装在陆地上的NREL近海5兆瓦基线风力机。其目的是建立不受水动力载荷或平台运动影响的基准风力机响应。第二次载荷分析是同一风力发电机安装在海上的浮式ITI Energy barge平台上。我在两个分析中使用了相同的风力机控制系统。使用相同的涡轮模型(相同的从叶尖塔基地)和控制系统——和离岸负载设置规定的先例,因为设计过程中设计标准IEC 61400 - 3[34]支持派生海上风力机的设计与陆基风力机。
最后,对于安装在浮式barge平台上的风力发电机,必须进行设计修改,以确保达到良好的性能,并保持结构的完整性。实际上,我的负载分析只是迭代设计过程中的第一步。从最简单的概念(即这是一个安装在海上驳船上的陆上风力机) 在最终的设计中可以避免不必要的复杂。将浮式系统的响应与安装在陆地上的涡轮响应进行对比,使我能够量化在风浪联合荷载作用下,涡轮与浮式barge平台之间的动力联轴器所带来的影响。这一比较点出了在哪些地方必须进行修改,以达到一个适合浮动系统的设计。此类设计修改必须通过后续项目中的附加负载分析迭代来解决。
我使用IEC 614001 - 1陆基涡轮设计标准[33]和IEC 614001 - 3海基涡轮设计标准[34]作为初步负荷分析的指南。614003设计标准仍处于草案阶段,关于其设计要求的规定的讨论还在继续。此外,614003设计标准明确规定,本标准中规定的设计要求不一定足以保证海上浮式风力机的工程完整性[34,p.7]。然而,为了进行初步的负荷分析(主要是可行性研究),我假定所述的设计要求是充分的。我没有试图确定其他可能的特定的平台设计条件。
在第5.1节中,我将概述和描述陆基和海基载荷分析中的模拟运行。然后,第5.2节我们讨论了如何处理负载分析数据。第六章给出了荷载分析结果。
5.1设计荷载工况
荷载分析包括通过运行一系列设计荷载工况(DLCs)来验证风力机的结构完整性,以确定在机器的预期运转周期内极端(极限)和疲劳荷载(即力和位移)。风力涡轮机的主要部件,包括叶片、传动系统、机舱和塔架,以及浮式系统的系泊索,都要检查载荷。所需的设计荷载工况包括基本的设计驱动情况,如正常工作条件、启动事件、关机事件、暂停或空转状态,以及适当的正常和极端外部条件和可能的故障场景。
每个IEC设计标准都规定了大量的设计荷载工况。对于这个初步的荷载分析,我认为没有必要运行设计标准规定的所有设计荷载工况;相反,我使用了一个子集,消除了疲劳类型的设计荷载工况,只处理预期的最终荷载。这一疏忽源于陆基和底部固定的海基风力机的标准设计实践,其中结构被配置为在检查疲劳之前承受极限荷载[96]。然而,由于疲劳往往决定着风力机的设计,因此在后续的工程中,必须通过处理省略的疲劳型设计荷载工况来评估平台运动对风力机疲劳损伤的影响。
如3.1.6节所述,参考涡轮控制系统不包含启停顺序逻辑,所以我去掉了3.x、 4.x,和5.x设计标准中定义的设计荷载工况。但是,我确实考虑过2.x设计荷载工况中的故障场景之后的关机。我也忽略了与运输、装配、维护和修理有关的8.x设计荷载工况的案例。我省略的四个设计荷载工况可能控制了一些历史上风力机的最终荷载,但我认为省略它们是合理的,因为根据我使用陆基涡轮机的经验,它们并没有控制最终荷载。
剩余的最终类型设计荷载工况包括以下设计情况:电源生产, 1.x设计荷载工况;发生故障时发电, 2.x设计荷载工况;暂停(空转),6.x设计荷载工况;有故障停车,7.x设计荷载工况。表5-1总结了我选择的


