英语原文共 11 页,剩余内容已隐藏,支付完成后下载完整资料
吸湿沉降的路堤数值模拟
摘要:本文采用基于有限差分的计算机程序实现了巴塞罗那基本模型(BBM),以模拟不饱和土壤的润湿行为。使用分析解决方案验证了BBM实施,并且使用已验证的模型来模拟完全饱和的压实填充路堤的润湿诱导影响,作为设计的最坏情况。结果表明,路堤顶面可能会发生相当数量的总沉降和差异沉降。此外,路堤的上段有起伏的倾向,而较大的约束应力下的下段可能由于润湿而塌陷。随后的参数研究结果表明,初始水分含量,路堤高度和坡度角对湿润诱导变形和不饱和路基稳定性有重要影响。
作者关键词:不饱和土堤;润湿引起的沉降;坍方;数值模拟
介绍
压实填筑堤坝的沉降通常由两个主要部分组成:自重沉降和润湿沉降。根据初始水分含量,重力沉降是由重力作用下的压实填料的压缩造成的,这可能相对较快地发生。然而,通常称为崩塌沉降的湿润沉降通常在施工后发生,并且可能是长期的沉降问题,这取决于润湿速率(Miller等人2001)。堤防中的压实土壤通常处于不稳定状态。堤防填埋过程由于水位上升,降雨量大,淹水量大,蓄水池蓄水等原因而发生。由于基质吸力的损失,水渗入可导致路基内的压实填料和剪切破坏过度沉降。湿润引起的堤防沉降是世界各地普遍存在的问题,造成对支撑结构(例如,桥梁接近板和栏杆墙),路面行人和墙壁边坡破坏的结构造成损坏。堤防崩溃解决问题的后果使纳税人每年修复和重建数亿美元。
已经进行了许多研究,以研究使用常规实验室的不饱和土壤的压缩行为
测试和离心机测试(Zornberg和McCartney 2010; McCartney和Zornberg 2010; Hoyos等人2012; Mun和McCartney 2015)。然而,关于润湿诱导体积变化行为的研究比较少(Houston等,2001; Sun et al。2007; Cerato et al。,2009)。 Lawton等(1992)确定几乎所有类型的压实土壤在适当的条件下都可能容易崩溃。影响给定压实土壤的崩塌行为的最重要因素是初始水分条件,初始干密度和应力状态(Lawton 1986)。实验研究,主要涉及渗透测试,已经进行了确定压实土壤的崩溃潜力,这通常与各种参数相关,包括垂直应力湿润,初始水分含量,初始干密度,塑性指数(PI)和粘土大小分数。 ,已经预测了现场压实填料的崩塌沉降(Houston等人,1988; Basma and Tuncer 1992; Lim和Miller 2004)。然而,在这些经验相关性的基础上的崩溃预测模型通常被过度简化,因此不够准确。 Miller et al。 (2001)进行离心机试验,以模拟在相对压实(RC)下压实的20米高的粉质路基(90%至95%),水分含量在最佳含水量(OMC)的2%至5%之间。进行了实验室测试,以确定用于预测沉降的土壤参数。结果表明,使用经验相关性的预测的崩溃沉降低估了原型路堤中的测量值,因为一维预测模型无法正确解释堤坝的二维性质。然而,由于模型复杂性,这些复杂的结构模型很少应用于现实的计算机程序中(BBM)(Alonso等,1990),巴塞罗那基本模型(BBM)(Alonso等,1990)是广泛使用的结构模型,已经在几个计算机程序中实施,以研究与不饱和土壤相关的实际工程问题(Alonso等人2005; Costa and Alonso 2009; Farias 和Cordao Neto 2010; Zheng et al。2013)。
在本研究中,BBM在有限差分程序Continua(FLAC)的快速拉格朗日分析(Itasca Consulting Group 2005)中实现,以模拟不饱和土壤的润湿行为。 使用分析解决方案验证了BBM实施,并将验证的模型用于模拟完全饱和的不饱和路堤的润湿诱导响应,作为设计的最坏情况。 进行了参数研究,以检查初始含水量,路堤高度和侧坡对润湿诱导变形的影响。 本研究的结果为改善不饱和条件下堤防设计和施工实践提供了更好的理解
在FLAC中实施巴塞罗那基本模式
BBM(Alonso等,1990)是一个结构模型,可以描述不饱和土壤的弹塑性行为,并捕获许多典型特征,如不同应力水平下的膨胀和塌陷,以及基质吸力增加剪切强度和预固结压力 Gens et al。2006)。 在本研究中,BBM在FLAC中通过扩展改性凸轮粘土(MCC)结构构模型计算机程序来解决基质吸力对不饱和土壤刚度和强度的影响。
BBM包括两个独立的应力变量:净应力(sigma;-)和基质吸力(-),其中sigma;是总应力,和分别是孔隙空气和孔隙水压力。 对于BBM的实施,做出以下假设:(1)孔隙空气压力相对于大气孔隙气压为零,这对于大多数自然地面条件是正确的(Sheng 2011),因此净应力相当于总 强调; 和(2)基质吸力是影响不饱和土壤在润湿过程中的刚度和强度的参数。 随后简要介绍了FLAC中FLM的实现情况,郑(2013)报道了更多细节。
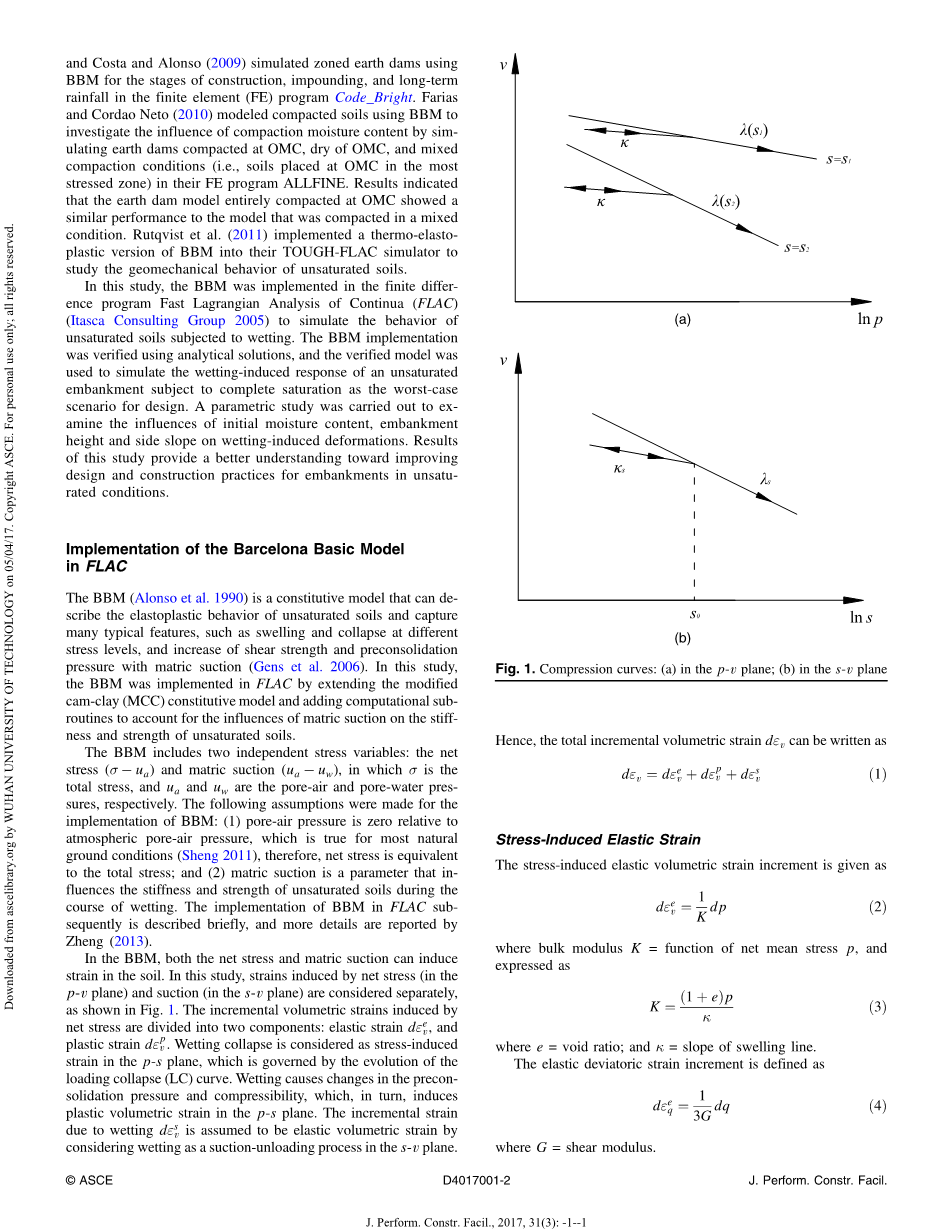
在BBM中,净应力和基质吸力都可以在土壤中引起应变。 在这项研究中,分别考虑了由净应力(p-v平面)和吸力(在s-v平面)诱导的菌株,如图1所示。 1.净应力引起的增量体积应变分为弹性应变v和塑性应变v两部分:润湿塌陷被认为是ps平面中的应力诱导应变,由应力引起的弹性变形 (LC)曲线。润湿导致重新固结压力和压缩性的变化,这又导致ps平面中的塑性体积应变。 由于润湿引起的增量应变被认为是弹性体积应变,通过考虑润滑 - 卸载过程 - 平面。
因此,总增量体积应变可以写为
(1)
应力诱导弹性应变应力引起的弹性体积应变增量为
(2)
其中体积模量K =净平均应力p的函数,并表示为
(3)
其中p-q平面f中的屈服面被定义为
(4)
(5)
则
(6)
(7)
(8)
whereq =偏置应力; M =斜率临界流化床(CSL); s =吸力; ps =吸力内聚力; p0 =吸入时的固结压力; k =描述吸附凝聚力增加的参数;P 0 =饱和状态的预固结压力; pc =参考压力; lambda;eth;0THORN;=饱和条件下正常固结线(NCL)的斜率; lambda;eth;sTHORN;= NCL在吸力下的斜率; 和r和beta;=控制土体刚度作为吸力变化的参数
流量BB实现,相关流量用于计算塑性体积应变增量dεpv。一旦屈服发生,饱和条件下的预固结压力的演变p? 0由硬化规律定义为
(9)
吸引诱导应变对于润湿引起的变形问题,润湿路径是一个吸力卸载过程。 在润湿期间的任何时刻,电流吸力等于或小于过去土壤经历的最大吸力s0。 因此,土壤仍然存在于弹性区域中,在流动过程中残留.Rutqvist等 (2011)通过在净应力中加入等效平均应力增量来确定吸力诱发应变,这也在本研究中采用并适用于FLAC中的实施。 抽吸引起的体积应变dεsv计算为
(10)
其中Ks =等效抽吸体积模量定义为
(11)
其中kappa;s=与吸引力弹性应变相关的可压缩参数; 和patm =大气压力。 等效平均应力增量为
(12)
这通过将等效应力增量dps加到正常应力sigma;xx,sigma;yy和sigma;zz上来实现。式。 (12)表示等效应力增量与基质吸力的变化成正比。 因此,净平均应力由于润湿期间的吸力损失而降低,这导致卸载并因此导致土壤膨胀。 然而,预固结压力,刚度和强度也随着吸力降低而改变,这可能会诱发
崩溃应变。 所有这些影响都有助于整体体积变化对不饱和脂肪变化的影响,肿胀或皱缩,这取决于最后的湿润程度。 通过将初始值的基本吸力从规定的减量度减小到目标值来模拟湿润引力学的研究。
FLAC中BBM实施的验证
在文献中使用分析解决方案验证了FLAC中实施的BBM。 在研究润湿引起的变形问题时,润湿路径是主要的焦点。 Alonso等人 (1990)报道了BBM预测案例研究(简称案例1),其中包括三个明确的润湿路径。 在本案例研究中,对参考土进行各向同性压缩。 如图所示。 如图2所示,三个应力路径(1,2和3)从p = 150开始,s = 200,结束于p = 600kPa,s = 0kPa。 三个润湿路径分别在150,350和600kPa的限制压力下发生。
Alonso等报道的参考土壤的BBM参数 (1990)总结在表1中。在变形控制载荷下,对参考土进行了一系列单元素三轴试验。 润湿路径通过在1kPa减量中从200kPa的初始值降低至零来计算吸力。 这种方法不是耦合的水力机械分析,而是可以以相对简单的方式模拟吸力的减少。
结果比较如图3所示。图3表明预测和分析结果总体符合良好。 润湿路径1发生在弹性区域内并引起少量肿胀。 润湿路径2在土壤各向同性压缩至350kPa的净平均应力之后开始,导致比容量减少0.5(从1.84到1.79)。 润湿路径3以密封压力600kPa开始,并产生0.7的特定体积减少(从1.76到1.69)。 在弹性区域,土壤在低应力水平下经历少量肿胀。 然而,在高应力水平下产生崩溃。 此外,塌陷的幅度随着净平均应力的增加而增加。
模拟不饱和路堤
验证的数值模型用于研究不饱和路堤在施工和润湿阶段的润湿作用响应。 进行了完全饱和条件的数值模拟,作为堤防设计的最坏情况。 提出并讨论了模拟结果,包括路堤表面和中心线沉降,以及斜坡侧向位移。
数值模型BBM参数的确定通常需要吸力控制测试。 Alonso等人 (1990)提出了三轴状态下的应力路径来确定模型参数。 Gallipoli等人 (2010)和Zhang and Xiao(2013)也开发了选择BBM参数的方法。 在本研究中,选择具有校准BBM参数的压实高岭土(Josa 1988; Alonso等人,1990)作为对比的补充。根据统一的土壤分类系统(USCS),压实的高岭土发芽和分类。 该压实高岭土的BBM参数总结在表1中。
图4显示了堤防模型的几何和有限差分网格。 路堤填筑高10米,坡度为1V:2H,基础土深5米。 堤坝的一半由于对称而被模拟。 路堤中心线位于模型边界左侧。 路堤的底部和顶部分别为30米和10米宽。 横向边界在水平方向固定,但允许垂直运动,而底部边界在水平和垂直方向都是固定的。
堤坝填充物采用初始吸力为100 kPa的BBM进行建模。在粉砂土中已报告了相当的吸力值,压实度达到近50%的最大干燥密度的95%(Garcia2010; Hatamietal。2013)。使用Mohr-Coulomb模型对基础土进行建模,并假设其处于饱和状态,因此对润湿过程中路基的响应没有影响。在第一阶段,地基土在重力应力下达到平衡。然后在10座升降机的基础土上建造起始吸力值为100 kPa的10 m高的路堤。最后,通过将初始土壤吸力减少到零,并以选定的减量值来模拟路基的润湿过程,以表示完全饱和的条件。考虑到计算时间和精度,最终在一系列灵敏度分析之后选择10 kPa的抽吸减量值来模拟润湿路径。因此,在润湿过程中,整个模型在初始吸力值为100 kPa至10的循环中达到临界平衡状态。
图5显示了在自重加载和饱和后的平衡条件下路堤模型中的位移矢量。 堤坝中心线顶部的沉降在自重压缩下为69 mm。 堤防完全饱和后,沉降达到262毫米,比起自重的初始沉降量增加近三倍。 本研究中的润湿诱导变形定义为由于润湿超过自重负载下达到的大小而导致的变形。 因此,路基顶面中心线预测的湿润沉降为193 mm。 图。
图6表示不同阶段路基表面的沉降。在自重加载下,路堤表面沉降约60 mm,顶面中心线与边缘之间的差异沉降为23 mm。堤岸完全饱和后,路基沉降约为250mm。因此,湿润沉降的大小约为190 mm。图。 5也表明路堤最大沉降发生在中线,而最低沉降发生在两段边缘。完全饱和后,中心线路堤的沉降比边缘大54 mm,导致可测量的差异沉降量。湿润诱导的总沉降和偏差设定在其内部可能对上覆结构和路面造成重大损坏。
图7显示了沿着不同阶段的堤防中心线的沉降。由于模型是逐步建立的,因此每个升降机的位置都报告了累积位移。最大沉降发生的高程从饱和荷载下的地基土上方5米移至饱和后7米。湿润引起的沉降在堤坝底部7m处显着增加,但沿着路堤的剩余顶部保持基本恒定(与最大值相比仅减少1mm)。不饱和土壤的重要特征是在土壤表现出低应力水平下的膨胀行为和高应力水平下的塌陷行为。
图8示出了p-s平面中不饱和土壤的重要特征是在土壤表现出低应力水平下的膨胀行为和高应力水平下的塌陷行为。图。图8示出了p-s平面中的润湿路径和负载塌陷(LC)屈服曲线。在初始吸力si时,相应的收率曲线为LCi。土壤元素和弹性区域,而屈服曲线。土壤元素A在整个润湿过程中保持在弹性范围内,因此元素A因润湿而膨胀。在这个例子中,路基中压实土壤的顶部3m区域在润湿期间保持弹性。因此,在该地区的这一地区发生膨胀,导致累积湿润沉降(1mm减少)减少。土壤元素B在初始抽吸时保持弹性,但在润湿过程中预固结压力降低。当固结压力降低到当前的电流应力(即,B达到屈服曲线LCi)时产生,然后在完全饱和时开始移动并达到LCB。当在自重负荷下经受足够大的应力时,初始吸力产生的土壤元素C,在饱和时,产量
全文共9924字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[143253],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。