
英语原文共 11 页
超跨径斜拉桥桥面系统的最佳组合
摘 要:主梁的巨大轴力对超跨斜拉桥的设计提出了挑战。为了减少梁的自重,传统的正交异性钢板(OSD)系统由于其高强度重量比而被广泛采用,这可能产生疲劳问题。本文通过设计一个主跨为1,480 m的斜拉桥,研究了不同桥梁和桥面系统的最佳组合。研究了两种不同的桥梁系统:传统的斜拉桥系统和带有交叉斜拉索的部分地锚式斜拉桥系统(新的桥梁系统)。此外,在每个桥梁系统中,研究了三种不同的面板系统:OSD系统,由OSD系统和超高性能混凝土(UHPC)层组成的复合面板系统,以及UHPC华夫板面板系统。开发并分析了六个方案的有限元(FE)模型。比较了六个方案的静态、动态和经济性能。进行复合和UHPC华夫板系统的模型试验以确保设计的可行性。与传统的桥梁系统相比,新的桥梁系统在主梁上具有小得多的轴向力,更大的纵向刚度和经济优势。在车道荷载下,使用UHPC华夫板面板系统的主梁产生的应力幅度远低于其他两个面板系统的主梁。与OSD系统相比,复合和UHPC格栅板系统在使用年限成本方面是有利的。因此,建议将新桥系统和UHPC华夫板面板系统相结合作为最佳设计方案。
关键词:斜拉桥;面板系统;超高性能混凝土;静态性能;动态性能;经济;使用年限
引言:与悬索桥相比,斜拉桥具有刚度大和空气静力稳定性等优点。在二十一世纪, 人们建造了几座主跨1000米的斜拉桥(如Russky桥、苏通桥和昂船洲大桥)。现有的超跨径斜拉桥采用传统斜拉桥系统与传统正交异性钢桥面(OSD)系统相结合的方案。然而,梁的巨大轴向力限制了传统斜拉桥系统的经济跨径。梁的巨大轴向力需要较大的横截面面积和较厚的钢板,从而增加了梁的自重力和轴向力,增加横截面面积和使用较厚的钢板也会增加成本。同时,对于大跨度桥梁, OSD 系统由于具有较高的强度重量比,有效地降低了梁的自重,从而得到了广泛的应用。然而,在车轮载荷作用下,OSD系统的大局部变形会产生疲劳问题, 这对结构的耐久性提出了挑战。
因此,人们最近的研究集中在两个领域:改进桥梁系统并加强面板系统。在桥梁系统方面,邵旭东等人提出了一个超跨部分地面锚索斜拉桥的概念设计,该斜拉桥有交叉斜拉索(以下简称新桥系统)。新型桥梁系统通过在中间区域穿过斜拉索有效地减小了梁中的轴向力。交叉缆索区域在主梁中几乎不产生水平力,因为在交叉缆索中张力的水平分量彼此平衡,并且交叉缆索在后跨处锚固到地锚。在面板系统方面,邵旭东等人提出了由OSD系统和超薄超高性能混凝土层 (以下简称 1型新型面板系统)组成的复合甲板系统,具有显著意义。在不显著增加自重的情况下,增加OSD系统的刚度。该复合体系可将钢板中的应力振幅降低40% 以上,并解决 OSD 系统的疲劳问题。Aaleti等人还提出了UHPC华夫面板系统 (以下简称2型新面板系统), 与传统的钢-混凝土复合面板系统相比,自重相对较低。邵旭东介绍了1型和2型新面板系统的详细设计和施工原则。由于研究将桥梁和桥面系统分离, 需要研究超跨径斜拉桥不同桥梁和桥面系统的最佳组合。
在前人研究的基础上,本文通过设计主跨1480米的斜拉桥,探讨了超跨斜拉桥的优化设计。本人主要考虑了两个方面: 桥梁系统和面板系统。研究了两种不同的桥梁系统: 常规斜拉桥系统和新的桥梁系统。针对每个桥梁系统,讨论了三种不同的桥面系统:传统的OSD系统、1型新面板系统和2型新面板系统。共研究了六种不同的组合(表1)。苏通大桥、虎门大桥和盛天大桥在设计这六个方案时被引用。利用 Ansys 软件建立并分析了六种方案的有限元模型。通过充分的结构分析,研究了六项方案在静载、交通负荷和温度效应下的性能。通过Ansys 中箱梁的局部模型,对1型和2型新型面板系统在服务车辆荷载作用下的应力水平进行了检查。对两个带钢筋的新面板系统进行了全面模型试验,以确定UHPC在两个新面板系统中的开裂强度。此外,模态分析还证明了这六个方案的动态特性。最后, 通过材料消耗估算,完成了六项方案之间的经济比较。
表1 六种组合的总结
计算模型
为了比较性能和经济性, 六个方案中的每一个都一致采用了1480米的主跨度长度。在给定桥梁系统内的三个方案之间,一般结构大小保持不变;设计之间唯一的变量是面板系统。这六个方案的整体结构和梁设计细节,可参考苏通大桥。1型和2型新面板系统的设计以虎门大桥和盛田大桥的面板设计为参考。与参考文献相比,钢板和UHPC层的厚度保持相同或根据完整结构分析确定的应力水平而增加。在恒载、交通荷载和车轮荷载的综合作用下,对UHPC的应力水平进行了检查,以确保新面板系统的安全。
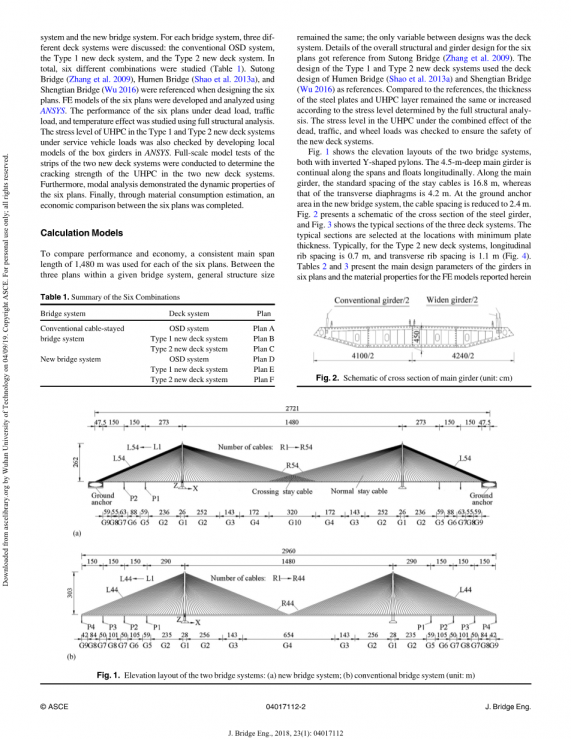
图1显示了两个桥梁系统的高程布局,这两个桥梁系统都有倒置的y形桥塔。4.5 m高的主梁沿跨度连续延伸,并纵向浮动。沿纵桥方向, 固定缆索的标准间距为16.8米,而横隔板的标准间距为4.2米。在新桥系统的地面锚固区,缆索间距降低到2.4米,图2给出了钢梁横截面的示意图,图3显示了三个面板系统的典型截面。典型的截面是在板厚最小的位置选择的。通常情况下,对于2型新面板系统,纵向肋间距为0.7米,横向肋间距为1.1米(图4)。表2和表3列出了本文所报告的六个方案中的梁的主要设计参数和有限元模型的材料特性。
对于Ansys中结构完整的有限元模型,各种元素类型用于不同的组件。梁189用于模拟梁和塔架。斜拉索是使用Link180模拟,并且基于恩斯特方程考虑了自重对斜拉索刚度的影响。考虑到横隔梁对动态特性的影响,利用质量21对横隔梁进行了模拟。最后,沥青覆盖层被认为是静载而不考虑其结构贡献。单元应力是从Ansys中为每种类型的单元生成的单元表中读取的。在边界条件下, Ansys中的横穿悬架线端受到了地面锚杆纵向、横向和垂直运动的严格限制。主梁在桥墩
和地锚处有垂直支撑, 并与每个塔架中最近的节点耦合,以抑制垂直运动、横向运动和扭转。桥塔底处节点的所有自由度都是固定的。
图1 两个桥梁系统的高程布局:(a)新的桥梁系统 (b)传统桥梁系统(单位:m)
图2 主梁横截面示意图(单位:厘米)
图4 2型新甲板系统的平面图
静态效果
静力荷载下的性能
邵旭东等人表明,在新的桥梁系统中,由于交叉缆缆和地锚系统的原因, 桥塔附近梁的轴向力减少。在静载作用下,表4列出了梁的轴向力和顶部和底部边缘的应力。对于相同的桥面类型, 新桥梁系统梁的最大轴向力比传统桥梁系统低31–35%。这种下降降低了整个桥梁的自重,减少了材料消耗, 延长了斜拉桥的经济跨径。在第一次系统分析中,表4显示六个计划的梁在静载作用下具有相同的应力水平, 这意味着它们的材料消耗可以合理比较。同时,OSD系统和1型新面板系统产生的最大轴向力水平几乎相同 (相差4% 以内),而2型新面板系统则导致最大轴向力提高12–17%。这种增加主要是由于2型新面板系统的自重较大造成的。
移动荷载下的性能
中华人民共和国交通部 (2015年) 将车道荷载定义为均布荷载 (10.5 KN/m) 和集中荷载 (360 KN) 的组合。表5比较了六个方案在交通荷载下的梁的顶部和底部边缘的应力振幅。由于1型新型面板系统的UHPC层比2型新面板系统的 UHPC 板薄 60–70%, 因此 B方案和 E方案的整个梁的刚度小于C 和 F 方案中的刚度。因此, 在交通荷载作用下, 1 型新型桥面系统梁的应力振幅接近 OSD 系统, 而2型新型桥面系统梁的应力振幅降低了60% 以上。特别值得注意的是, 这里的应力振幅是由全球交通负荷引起的;下一节报告了面板系统在局部车轮荷载下的应力。
在恒载和交通荷载的综合作用下, 六个方案中的桥塔都处于压应力下;最大压应力为12.7 MPa。满足小于22.4 MPa 的要求。六个方案中缆索的最大拉应力为 758 MPa, 比允许的设计应力高 1.8%, 容许误差在5% 以内。
局部车辆荷载下桥面板的分析
在这项研究中研究了1型和2型新型面板系统中 UHPC的应力水平。在 Ansys中开发了两个新面板系统的局部模型, 以确定第二系统应力。两个新的面板系统使用它们的典型部分进行模拟, 这是最不利的情况。在纵桥方向上, 25.2 米的跨度设置了七个横隔板,而对于横截面, 建立了全梁截面。在Ansys中,分别用 solid45 和 shel63 模拟UHPC和钢板。在局部模型中, 由于沥青覆盖层的弹性模量较低,未考虑其复合作用。因此,与实际现场条件相比,本文报告的分析结果对UHPC中的应力是保守的。图5说明了局部模型的边界条件,其中横隔梁和腹板之间的接头受到垂直刚性支撑的约束。图5还介绍了这两个新面板系统的模型细节。
根据中华人民共和国交通运输部(2015年)的数据,车辆荷载被视为两辆汽车, 每辆车有五个车轴,总重量为550 KN(图6)。为了研究UHPC层在车轮荷载作用下最不利的情况,须考虑纵向两种不同的情况和横向的三种不同情况(图7)。在全球范围内, 每个新的面板系统模拟了6个综合案例。在每个全局情况下, 都包括了统一车轮荷载的三个局部详细的横向位置 (图8)。在这些组合的基础上, 表6和表 7汇总了UHPC层在车轮荷载作用下纵向和横向的最大拉压力和压应力。在纵桥方向上, 在恒载、车道荷载和车辆荷载的综合作用下, 1型新面板系统的 UHPC 最大拉压力和压应力分别为7.3 MPa 和27.3 MPa,而2型新甲板系统的最大拉压力和压应力分别为14.9 MPa 和30.2 MPa。在组合效应下,2型新型甲板系统的最大拉应力出现在面板系统的底部边缘, 顶部边缘的最大拉应力为 6.0 MPa。
温度效应
由于本文主要研究了整个系统的基本性能,因此认为温度效应是适用于整个结构的均匀温度变化。非均匀加热下梁的性能需要进一步研究。假设结构是在20℃下构建的,最高和最低环境温度分别为40和0℃。图9以 A方案和D方案为例, 介绍了它们在整个系统内均匀升温下呈现出的结构变形。在传统的桥梁系统中, 在温度升高的情况下,主梁趋于膨胀,因此锚定在主梁两端附近的缆索明显收紧。这些紧固的缆索导致桥塔朝横向侧向变形,从而减少了梁的中跨偏转。相反, 在温度荷载作用下,新桥体系中的塔架变形受到锚定锚索的限制,导致主梁发生较大的挠度。因此,在均匀的温度变化下,传统桥梁系统的中跨挠度 (0.07–0.09 米)小于新桥梁系统(0.46–0.52 米,即l/3,217–l/2,846,其中l=主跨长度)。需要指出的是, UHPC与钢材在热膨胀系数上的差异会在1型和2型新面板系统中造成额外的内应力。。UHPC的这种效应和准确的热膨胀系数需要进一步研究。
两种新型桥面系统的带钢筋模型试验
对两种新型桥面系统的带钢筋模型进行了测试, 以验证设计的可行性。邵旭东等人报告了1型新面板系统的测试程序和结果。1型新型甲板系统中 UHPC 的开裂应力为 42.7 MPa, 是计算出的最大拉应力 (7.3 MPa) 的 5.8倍, 表明在1型新型甲板系统中, UHPC具有抗腐蚀性。本文仅对2型新型面板系统的带钢筋模型进行了测试。
对于2型新型桥面系统的带钢筋模型,采用了典型的截面尺寸,这是最不利的情况,与局部有限元模型一致。图10显示了带钢筋模型的高程布局和横截面。截面示意图还显示了带钢筋模型的加固布置。带钢筋模型的跨度为3500毫米,总长度为3, 700 毫米。所使用的钢筋等级为 HRB400,屈服强度为400MPa。
在室温下进行湿固化48小时, 然后在90–100℃ 蒸汽固化 48小时,防止早期收缩开裂。UHPC中的钢纤维在两端被钩住, 抗拉强度为2700 MPa, 按体积计算占复合材料的2.5%。纤维长13毫米, 直径0.2 毫米。铸造了100毫米立方样品和100times;100times;400—mm横梁 (图11)。基于3个立方体试样试验的基础上, UHPC 的抗压强度为139.2 MPa,在三束三尖弯曲试验的基础上,其弯曲强度为 32.3 MPa。
对带钢筋模型进行单调的三点弯曲试验(图12)。为了确定顶部边缘的开裂强度, 通过将带钢筋模型倒置进行了负弯曲试验。UHPC的开裂强度(sigma;w0.05 ) 被定义为引发宽度为0.05mm的裂纹的应力水平。在开裂宽度超过0.05 mm之前, 复合材料具有弹性,保证了复合材料的耐久性。此外, UHPC中的纤维拉拔和强度退化始于裂纹宽度达到0.3 mm(Franccedil;aise De Geacute;nie civil 协会,2002年),这远远超出了规定的裂纹强度(sigma;w0.05 ).根据带钢筋模型的正弯曲试验,2型新型桥面系统底部边缘的开裂强度为19.4 MPa。在负弯曲试验的基础上,顶部边缘的开裂强度为13.8MPa。
Aaleti 等人报告说,放大的AASHTO服务卡车车轮荷载 (21.3千磅)单调地应用于UHPC华夫板面板,并形成裂纹,最大宽度为0.05 毫米。然后,华夫板面板承受了1000000次循环的疲劳载荷,荷载在2至21.3千磅之间。未观察到额外的裂缝或裂缝延伸。此报告表明sigma;w0.05是一个安全的应力水平,不会产生严重的疲劳问题。在有限元模型的组合效应下,2型新型面板系统 (6.0和 14.9 MPa) 顶部和底部边缘的最大拉应力都小于在模型试验(13.8和19.4MPa)中确定的sigma;w0.05,从而证明了设计的可行性。
基本动态性能
利用Ansys进行模态分析, 得到了六个方案的前20种模态。表8和表9列出了首次出现不同类型振动的模式。在同一桥梁系统中,尽管两个新面板系统箱梁的刚度大于带有OSD系统的传统钢梁,但由于两个新面板系统的方案的基本频率减少了增加自重。对于不同桥梁系统的比较,由于有了辅助墩,传统的桥梁系统比新的桥梁系统显示出更高的基频。因此,辅助墩的刚度贡献似乎高于交叉缆索系统,这与邵旭东等人一致。然而,由于新桥系统的交叉索系统,梁的纵向刚度得到有效增强。对于新的桥梁系统,梁的纵向浮动出现在第三种模式下,而对于传统的桥梁系统,
资料编号:[6012]
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


