英语原文共 24 页,剩余内容已隐藏,支付完成后下载完整资料
2.1应力集中
线弹性断裂力学(LEFM)可追溯到1920-1921年,当时格里菲斯提出了玻璃脆性断裂的能量方法。任何材料,包括非常光滑的均质材料,如玻璃,都含有缺陷。这些缺陷是应力集中的来源,可能导致材料的破坏远低于其理论强度。基于原子键势的正弦近似
其中是原子键应力间距图中的峰值应力,r是原子原始晶格间距r0的增加,因此可以计算晶体固体的理论强度,从而得出(Kelly和MacMillan 1986):=
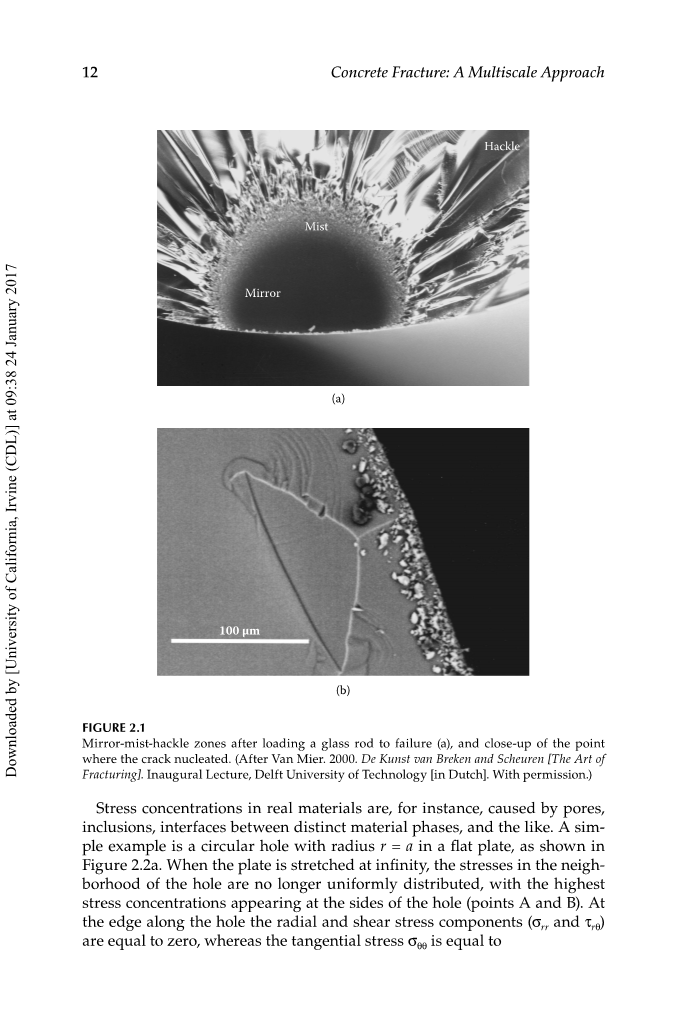
杨氏模量E将应力与应变联系起来,遵循sigma;=E.ε=E.x/。例如,对于耐碱玻璃纤维,杨氏模量E=70 GPa(Gupta 2002),根据方程式(2.2)预测的理论强度将为=23 GPa,而实际上约70 MPa是在一根纤维上测量的。纤维的直径对其强度影响很大。表面缺陷导致应力水平远低于最大可达到值时过早失效。在图2.1a的玻璃棒中,裂纹似乎是从镜面区域底部的小白线形成的。该杆是一种简单的现成产品,其外部受到严重污染,如图2.1b所示。裂纹因缺陷而成核,并似乎在开始时对称开始。经过相当平滑的镜区后,表面粗糙度逐渐增加到雾区和粗糙区.
图2.1
在加载玻璃棒至失效(图a)后,对裂纹形成的点进行近距离观察。(在范米尔之后。2000年。德昆斯特·范布雷肯和舍伦[压裂术]。德尔夫特理工大学(荷兰语)开幕演讲。在得到许可的情况下。)
例如,真实材料中的应力集中是由孔隙、夹杂物、不同材料相之间的界面等引起的。一个简单的例子是平板中半径r=A的圆孔,如图2.2a所示。当平板无限拉伸时,孔附近的应力不再均匀分布,最大的应力集中出现在孔的侧面(点A和B)。在孔的边缘,径向和剪切应力分量(和)等于零,而切向应力等于
图2.2
具有完美圆孔(a)、椭圆孔(b)和狭缝(c)的板。
-2cos2 (2.3)
这些直接从线性弹性理论推导而来, Timoshenko和Goodier(1970)给了完整的解决方案。项是外部施加的应力。很容易看出,沿孔边(theta;=pi;/2和3pi;/2)的应力是外部应力的三倍,孔上和孔下(theta;=0和pi;)的压缩应力等于–。因此,如果板料拉伸失效,实际测量的应力比没有圆孔的材料能承受的应力低三倍。
当孔的形状变为椭圆形时,应力集中变得更加严重(图2.2b)。当椭圆的半轴等于a和b时,a和b处的切向应力增加到
(2.4)
椭圆越平坦,应力集中越高,板的实测破坏应力越低。对于狭缝,即当b→0(见图2.2c)时,尖端的切向应力将变得无穷大(······)。这时,断裂力学就引起了人们的兴趣。狭缝引起的位移跳变应采用不同于经典弹性理论的方法。
2.2线弹性断裂力学(LEFM)
上述情况,即远场张力,导致了经典断裂力学中区别的三种断裂模式之一。在图2.3中
图2.3
三种断裂模式:(a)张开模式I,(b)面内剪切模式II,和(c)面外剪切模式III
描述了常见模式:开启模式或模式I、面内剪切或模式II、面外剪切或模式III。这三种模式的组合称为“混合模式”,例如,张力和剪切可以是模式I II或模式I III
在工程实践中,大多数的情况集中在模式一上。其他模式出现的频率较低,但仍然非常重要。裂纹尖端应力由Irwin(1958)导出,在这一过程中引入了一个新的材料常数,即应力强度因子K。显然,必须以某种方式处理其奇异性,将失效准则改为基于应力强度而不是应力的准则似乎是一种可行的方法。这本书中反复出现的一个主题是断裂的材料和结构方面的分离,这在欧文(1958)推导的方程式中很自然地出现。所以,这里的问题是无限大平板中的一个类似滑轨的机架,受到远场拉伸或剪切。在图2.4中,该情况与笛卡尔坐标系中近端应力的定义一起略述。三个应力分量的表达式现在已经很熟悉了。并且可以在许多教科书中找到;例如,参见Broek(1983)、Lawn(1993)和Suresh(1991)。由于我们需要第10章中的表达式,这里列出了主要方程,并总结了它们的特点。
图2.4:承受远场张力的无限长板中长度为2a的类滑动裂纹尖端。值得注意的是由极坐标(r,theta;)定义的P点的局部应力、和
对于模式I(拉伸或打开模式),P处的三个应力和位移为
平面应力=0,平面应变=nu;( ),==0,以及
平面应力为,平面应变为=0。
在等式(2.6)中,平面应力K=(3-v)/(1 v),平面应变K=3-4v;是I型应力强度因子,定义为=尺寸为MParadic;m。对于II型(平面内剪切模式),表达式或多或少相同:
平面应力=0,平面应变=nu;( ),==0,以及
平面应力为,平面应变为=0。
K的定义与等式(2.6)中的定义相同,是定义为=模式II应力强度因子。最后,对于模式III(平面外剪切模式)
=0
0
(2.10)
与其他模式一样,是模式III应力强度因子,即=.
表达式(2.5)–(2.10)仅在裂纹尖端附近有效。在前两项之后,用测角函数进行的展开被切断了;高阶项一般可以忽略,当然除了非常特殊的情况,我们在这本紧凑的书的框架中没有讨论这些情况。这些方程可以用如下的通用形式来表示
(2.11a)
(2.11b)
从上面的方程可以清楚地看出,当r→0时,应力都表现出奇异性,这使得不可能使用应力准则来判断裂纹的扩展。应力强度因子K占据主导地位,现在是用来与临界值Kc进行比较以判断裂纹是否扩展的量。这是连续介质力学崩溃的地方。奇点的出现阻止了连续介质力学在类似于滑动裂纹的情况下的进一步应用,当然,除非像许多应用中所做的那样,不是计算某一点的应力,而是涂抹在更大的区域上,例如,我们在塑性裂纹尖端模型中看到的。压力的概念又回来了。从物理学的角度来看,很难想象奇点会真的发生。例如,在晶体固体中,裂纹尖端的原子键必须一次断开一个才能使裂纹扩展。如果原子势是正确的,那么随后的键断裂发生在有限的应力下(或者更确切地说,因为它是一个接触点)。正是从这个事实出发,开始怀疑连续介质力学在目前的应用是一个很好的做法。
裂纹尖端的应力,方程式(2.11a),部分取决于所谓的几何函数或重量函数。此函数取决于实际的试样/结构几何形状和边界条件,即裂纹尖端加载的情况。为了使问题更清楚,我们可以将应力强度因子写为:
K=f
式中, =a/W用于描述裂纹长度和试样尺寸的影响(用W表示,即试样在裂纹扩展方向上的宽度)。如图2.2c所示,对于无限大板中的中心裂纹,f()=1,K减小到。当试样具有有限宽度W时,几何因子近似为:
f (2.13) 在手册中可以找到几种精度不同的解决方案,如Tada、Paris和Irwi(1973)的解决方案,以及上述断裂力学教科书.
对于在铰链边界之间加载的单边缺口拉伸试样,Tada等人。(1973)给出几何函数f()的以下表达式:
对于所有a/W,其精度优于0.5%,而对于相同的单边缺口试样,但现在加载在固定边界之间(即,阻止试样加载端的旋转),则有更复杂的公式结果(Marchand、Parks和Pelloux 1986):
式中,F1和F2分别是法向载荷(式(2.14))和纯弯曲(见下文式(2.16))的几何函数,是无量纲裂纹符合性,包含法向载荷N、弯矩M、位移u和旋转phi;之间关系的所有信息。裂纹符合性只能用数值计算。包含解决方案的全部细节超出了本书的范围,感兴趣的读者请参阅Marchand等人。(1986年)。
方程式(2.15)中的函数F2可在Tada等人中找到。(1973)如下:
所有a/W值的准确度均优于0.5%。
使用简单表达式中的方程式(2.14)–(2.16),该表达式显示了相对裂纹长度对裂纹试样残余应力承载能力的影响(附录1中的方程式(A1.4)),有可能在单边缺口板的单轴拉伸试验中显示铰链与固定边界的影响。结果如附录2图A2.3所示,除软化曲线的尾部外,与混凝土断裂的实验观察结果一致;见图2.11和Van Mier、Schlangen和Vervuurt(1995)的相关结果。对于单轴拉伸试验中的边界旋转效应,可以进行类似的分析,表明线性弹性断裂力学产生的尺寸效应。LEFM预测较大的结构比几何相似的较小结构承载较小的荷载;见附录2。第六章和第九章分别讨论了边界旋转效应和尺寸效应.
上述Irwin的求解方法比Griffith的原始能量方法成功了几十年。在半径2a的区域释放的弹性能(总裂纹长度)与产生新裂纹区域2a.1所需的总表面能(假设含有滑动裂纹的板的单位厚度)是平衡的。弹性能可以用熟悉的形式表示
(2.17)
表面能是裂纹面积和比表面能gamma;的乘积
(2.18)
当能量释放率du/da超过表面能d/da的增加时,裂纹扩展发生:
=2 (2.19)
从而导致: (2.20)
式中,E是平面应力中的杨氏模量,在平面应变的情况下,必须用E=E/(1–代替。因此,当外加应力超过方程(2.20)给出的应力时,裂纹将扩展。请注意,除非特定边界条件限制裂纹,否则裂纹扩展是不稳定的。难点在于建立精确的表面能值。在文献中,常被临界能量释放率所代替,下标I是指模式I,它等于断裂过程中消耗的能量。临界能量释放率与Irwin的临界应力强度因子有关,因为我们可以很容易地从无限板(f()=1)的方程(2.12)和用代替的方程(2.20)导出。这导致了众所周知的关系:
(2.21)
2.3塑性裂纹尖端模型
欧文分析中的奇点导致了问题。连续介质力学的适用性似乎在弹性板中的类滑动裂纹的情况下受到限制。对于我们在本章开头提到的晶体固体,将原子势作为处理裂纹尖端过程的一种现实方法似乎是有意义的。方程式(2.1)的正弦原子势如图2.5所示。曲线下的面积是分离两个原子所需的能量,也就是破坏键所需的能量。这个能量实际上是所考虑的固体比表面能的两倍。基于这种潜在的粘聚力,Barenblatt(1962)设计了一个粘聚力裂缝模型,作为混凝土断裂力学后续发展的基础。原子键引起的内聚应力沿裂纹尖端附近的平面作用。
Barenblatt提出了一个重要的假设,即与整个裂纹的尺寸相比,裂纹尖端的粘结区应该很小。正如我们稍后所展示的,在对混凝土断裂模型的类比中,Hillerborg、Modeeacute;r和Peterson(1976)违背了这一假设。Dugdale(1960)提出了一个类似的塑性金属模型,其中Barenblatt使用的原子间内聚力被金属的屈服应力所代替。图2.6a、b显示了塑性裂纹尖端模型的原理。塑性区的尺寸为t,在长度为2a的无应力裂纹前推进。LEFM分析将导致无应力裂纹尖端的应力奇异性,但是,通过对粘结区(也称为工艺区)的假设,最大应力限制在屈服应力。在随后的分析中,假设总裂纹长度为2(a t),并且在较长裂纹的尖端区域,即在长度t的段上,闭合压力作用相等现在计算了两种应力强度:一种是裂纹尖端应力(假定在t上为常数),另一种是远场拉应力;见Broek(1983):
(2.22a)
arccos (2.22b)
当两个应力强度叠加时应取消的情况下,塑性裂纹尖端区域t的尺寸为:
t= (2.23)
关于裂纹尖端粘结区的实际应力分布,可以说有很多,关于塑性区的形状,可以说有很多。因为这对于后面的讨论不是非常重要,所以感兴趣的读者可以参考Lawn(1993)和Broek(1983)。然而,重要的是,由于加工区内任意楔形应力分布而产生的应力强度,这导致:
(2.24)
式中,表示裂纹尖端塑性区的应力分布,x坐标从裂纹中心的原点向裂纹尖端延伸,如图2.6b所示。图2.5中的原子间势是裂纹尖端楔形应力有用函数的一个例子;另见方程(2.1)。
2.4虚拟裂缝模型(FCM)
1976年,Hillerborg、Modeacute;er和peterson提出了上述混凝土断裂塑性裂纹尖端模型的扩展。所谓的“虚拟裂纹模型”包括一个与塑性裂纹尖端区相似的过程区,尽管应力分布不像Dugdale模型那样均匀,最大“屈服应力”要小得多,即等于混凝土的单轴抗拉强度;见图2.6c,与图2.6a相似,但裂纹尖端工艺区的变化除外。加工区会出现微裂纹,但
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[240276],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。