
英语原文共 20 页,剩余内容已隐藏,支付完成后下载完整资料
基于贝叶斯方法预测桥梁极端交通荷载效应及其在桥梁状态评估中的应用
杨宇,SMASCE1;和CS Cai,Ph.D.,PE,F.ASCE2
摘要:由于交通基础设施的老化和交通量的不断增加,桥梁的状态评估变得越来越重要,因为它为桥梁管理提供了有用的信息。可靠的状态评估取决于对桥梁剩余寿命中极端交通荷载效应(LE)的准确预测。在本研究中,引入贝叶斯方法来预测极端交通量LE,以提高预测的可靠性,并提出了利用预测的LEs进行桥梁状态评估的框架。为了演示所提出的方法,提出了一个使用结构健康监测数据对新的I-10双跨大桥(TSB)进行状态评估的案例研究。结果表明,与传统方法相比,贝叶斯方法可以提供更可靠的预测,因为它量化了参数中固有的不确定性,并将这些不确定性纳入预测。基于预测的交通量LE,使用所提出的框架评估桥梁的状况。DOI:10.1061 /(ASCE)be.1943-5592.0001357。copy;2019美国土木工程师学会。
关键词:负载效应(LE);预测;贝叶斯推理;桥梁状况评估。
简介:
桥梁是运输系统的重要组成部分。对于在役桥梁而言,由于经济增长导致的材料劣化和交通强度增加导致的阻力减少引起了对其安全性的严重关注。根据ASCE 2017年基础设施报告单(2017年),美国桥梁的平均年龄为43岁,许多桥梁的设计寿命已达到50年,需要重大修复或退役。同时,根据最近的USDOT报告“超越交通:2045”(美国运输部 2016)到2045年,货运量将增加40%以上,对现有的交通基础设施构成巨大挑战,其中许多基础设施不是为满足日益增长的需求而设计的。鉴于这些问题和挑战,近年来对在职桥梁的状况评估越来越受到关注(王等人。2016a, b).通过结构健康监测(SHM)进行桥梁状况评估可以提供有关桥梁性能和健康状况的实时信息,使桥梁所有者能够为桥梁维护和管理做出明智的决策。在过去的几十年中,对桥梁状况评估进行了大量研究,并提出了不同的评估策略(Aktan等。1997年; 夏等人。2008年; Ni等人。2012; Ma等人。2014; 夏等人。2017年).如果一座桥能够承受在设计寿命期间的预期负荷,那么它就被认为是安全的。因此,为了评估现有桥梁在其剩余寿命期间的安全状况,需要基于统计的方法来基于监测数据预测桥梁的极端交通负荷效应(LE)。
以前,已经开发了用于建模和预测桥梁的极端交通LE的不同方法。一些研究人员将最大流量LE的上尾部拟合到正态分布,并使用普通概率纸推断未来的极端LEs(诺瓦克1993年; 诺瓦克和香港1991).其他一些研究人员认为桥梁交通LE是一个静态高斯过程,并采用基于莱斯公式的平交方法来预测极端交通量LEs(陈等人。2015年; 克雷莫纳 2001).或许更常见的是,许多研究人员基于块最大值进行了极值分析(卡普拉尼 等。2008
年; 夏等人。2016)或超过阈值的方法(Crespo-Minguilloacute;n和 Casas 1997; 周等人。2016)预测极端交通LEs。O#39;Brien等人提出了对桥梁交通LE各种预测方法的综合评述。(2015).然而,大多数先前的研究没有考虑在极端交通LE的建模和预测期间分布参数的不确定性。在对极端交通LE建模时,通常存在两种类型的不确定性:随机和认知不确定性。提示性不确定性反映了自然过程的固有随机性,而认知不确定性是由缺乏知识引起的,例如有限的数据和建模错误。假设分布参数是确定性的,大多数预测方法仅识别偶然的不确定性。然而,监测数据的数量是有限的,因此当使用概率分布对数据建模时,认知不确定性可能是显着的。这种不确定性将导致预测的交通量LE的变化,如果忽略,可能导致对桥梁状况的非保守评估。卡普拉尼和奥布莱恩(2010)提出使用频率预测可能性来解释这种可变性,并发现预测似然方法给出了比经典返回周期方法大得多的寿命流量LE。贝叶斯方法为不确定性提供了一个自然的框架 - 健康的量化和预测。直接的结果来自贝叶斯推断是后验分布,也就是说,不确定性是在贝叶斯框架下正式引入的。
此外,贝叶斯方法将不确定性纳入其中通过后验预测分布预测未来结果,从而提供更可靠的预测。一个难点实现贝叶斯方法是高计算成本。然而,随着计算机技术的进步和强大的仿真技术,如马尔可夫链蒙特卡罗(MCMC)算法,贝叶斯方法在在现代统计中的流行。贝叶斯方法已经存在用于预测水文和气候学等领域的未来极端情况(程等人。2014; 利马和Lall 2009).然而,就作家的最佳知识而言,很少有关于直接使用贝叶斯方法预测桥梁极端交通LE的研究。奥布莱恩等人。(2015在使用模拟交通LE的比较研究中采用贝叶斯方法,并且发现贝叶斯方法对于不同的LE显示出不一致的预测性能。然而,在他们的研究中只考虑了分布参数的部分不确定性,并且由于有足够的模拟数据,认知不确定性非常小,以至于不确定性对极端交通LE预测的影响没有得到很好的强调。
本研究的目的是系统地引入贝叶斯方法来预测桥梁的极端交通LE,以提高预测的可靠性。首先介绍了极值分析和贝叶斯推理的理论。其次,提出了利用预测的交通量LE进行桥梁状态评估的框架。使用SHM数据对新I-10双跨大桥(TSB)的状态评估进行了案例研究,以证明所提出的方法。
极值分析的贝叶斯方法
极值分析
对于一系列独立且相同分布(IID)的运行随机变量的累积分布函数(CDF)是F(x),设Mn =max。基于 Fisher-Tippett-Gnedenko定理(费舍尔和蒂珀特1928年)如果存在一个实数序列,其中>0,那么有
其中G(x)=非简并分布函数,则G(x)必须采用广义极值(GEV),其CDF可写为
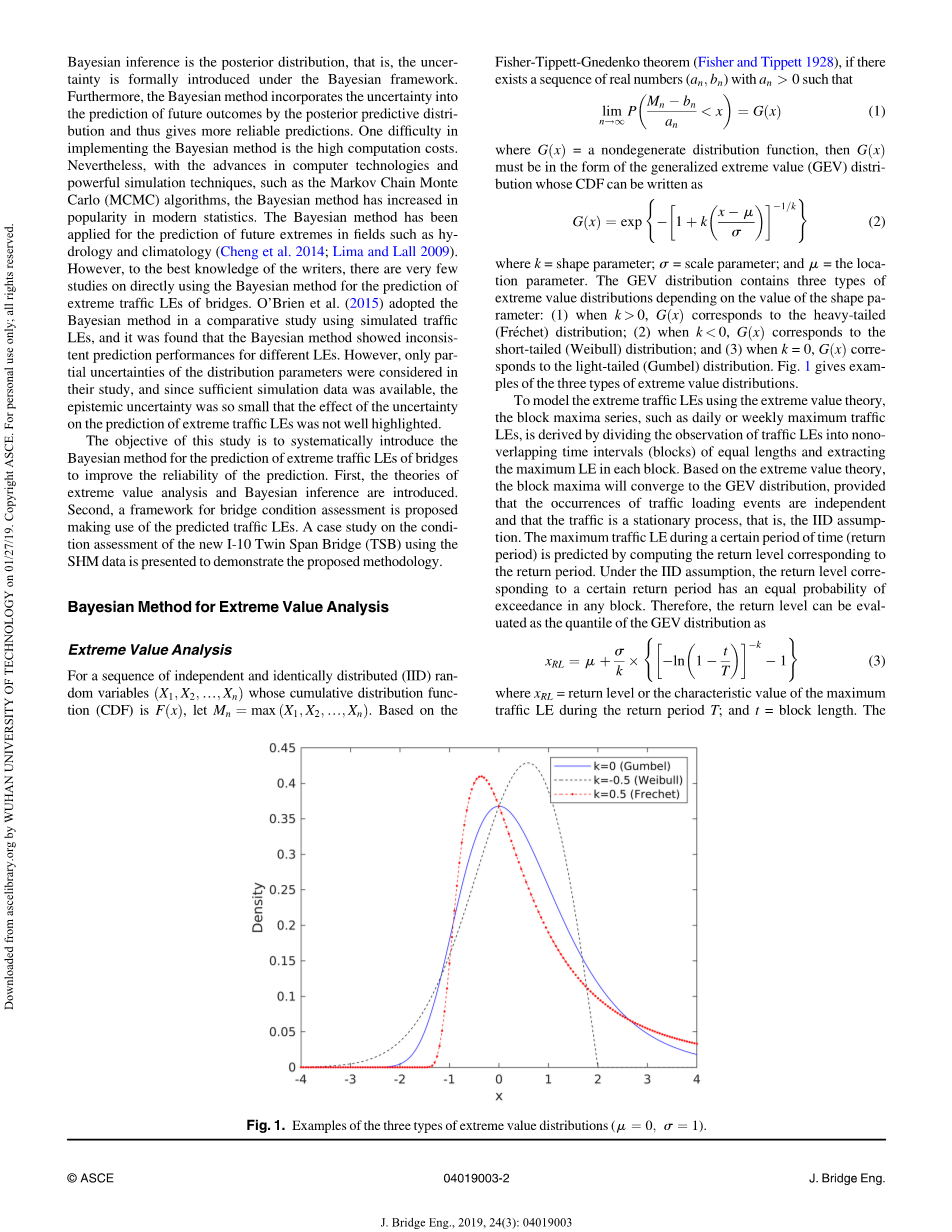
其中k =形状参数;s =比例参数;和m =位置参数。GEV分布包含三种类型的极值分布,取决于形状参数的值:(1)当kgt; 0时,G(x)对应于重尾(Frechet)分布;当k lt;0时,G(x)对应于短尾(Weibull)分布;(3)当k=0时,G(x)对应于轻尾(Gumbel)分布。图1给出了三种极值分布的例子为了使用极值理论对极端流量LE进行建模,通过将流量LE的观察值划分为相等长度的非重叠时间间隔(块)并提取最大LE来导出块最大值序列,例如每日或每周最大流量LE。在每个街区。基于极值理论,如果流量加载事件的发生是独立的并且流量是静止过程,即IID假设,则块最大值将收敛到GEV分布。通过计算对应于返回周期的返回水平来预测特定时间段(返回周期)期间的最大流量LE。在IID假设下,对应于某个返回周期的返回级别在任何块中具有相等的超出概率。因此,可以将返回水平评估为GEV分布的分位数如下
其中=返回水平或返回周期T期间最大流量LE的特征值;并且t=块长度。该预测的可靠性受到块长度的影响,因为返回级别通常在分布的尾部区域获得,其中分布通常不太准确。例如,如果块长度被选择为一天,那么50年回报水平对应于每日最大LE的分布的大约0.9999452分位数,这将需要每日最大LE分布的非常高的精度。从这个角度来看,增加块长度将使长期预测更可靠。同时,在选择块长度时也应考虑数据样本大小,因为块过大长度会使有效数据量太小。
图1.三种极值分布的例子(micro; = 0; б = 1)。
此外,在决策过程中需要考虑长期预测的可靠性。对于传统的极值分析最大值,首先将数据拟合到GEV分布,并且使用最大似然估计(MLE)获得分布参数的点估计。然后,通过使用等式1计算返回水平来进行预测。
贝叶斯推论
基于贝叶斯定理,后验分布推断的变量可写为
其中theta;= GEV 分布的参数;=参数的后验分布;;x = 数据;;=参数的先验分布;可表示为的似然函数
其中=非平稳GEV分布的概率密度函数(PDF);=第i次观察的值;Nt =观察次数。
在贝叶斯统计中,先验分布代表参数的先验知识,并且它独立于现有观察。一般而言,先验分布可以分为两种类型:信息先验和非信息先验。信息先验是基于通常从以前的研究和专家知识中获得的先验知识。另一方面,当很少或没有参数的先验知识已知时,采用非信息先验。非信息先验通常具有平坦分布以表示缺乏知识。在本研究中,引发信息丰富的先驱的困难源于高度特定地点的交通特征和桥梁行为。因此,采用非信息先验,并且具有宽支撑的悬垂均匀分布用作先验分布。具有宽支撑的悬垂均匀分布用作先验分布。应该指出的是,尽管先前的分配 对于每个参数,分布都是独立的,所获得的每个参数的后验分布将在推断之后依赖。
马尔可夫链蒙特卡洛(MCMC)抽样
公式(4)中的分母是一个多维积分仅取决于数据,其评估通常很困难。然而,这种积分的评估通常是不必要的,因为它可以被视为归一化常数,后验分布可以写成
马尔可夫链蒙特卡罗(MCMC)采样可用于使用等式(6)获得 GEV 参数的后验分布。 在这项研究中,采用Metropolis-within-Gibbs(MG)采样器。抽样程序描述如下:
1.将初始值分配给参数: ,其中k,б和micro;分别是GEV分布的形状,比例和位置参数;
2.对于i = 1:N(N =迭代次数),首先生成一个候选项形状参数的值k* 从正常的经验分布条件为 ,即, 其中=提案分布的比例。然后,计算k*的接受率为
对于 =形状参数的非标准化全条件分布,表示为似然函数和先验分布之间的乘积形状参数为
然后,样品u从均匀分布;如果u<min(1,),接受,有;否则,拒绝,有,;
3.生成比例参数的候选值,,从正常的建议分配条件,有,当=提案分配的规模,然后,计算的接受率为
同样的,=非规范化的完全条件比例参数的分布, 表示为
然后,样品u来自均匀分布U(0,1);如果u<min(1,),接受,有=;否则,拒绝,有=;
4.生成位置参数的候选值,,正常的建议分配条件是,有,当=提案分配的比例,然后,计算的接受率为
同样地,非规范化的完全条件位置参数的分布, 表示为
然后,样品u来自平均分布U(0,1),如果u<min(1,),接受,有=;否则拒绝,有=
5.重复步骤2到4,直到i到达N。在实践中,马尔可夫链的初始部分通常被丢弃,因为它可能不是目标的真实实现
图2.桥梁状况评估的大致框架。
由于初始值的影响而使用的分布仅使用链的稳定部分。此外,MG采样器的采样效率主要受提案分布规模的影响。在本研究中,MG采样器经过调整以获得最佳接受率,以实现有效采样(罗森塔尔2011).
后验预测分布
在贝叶斯统计中,最大流量LE的后验预测分布可以写成
其中y =预测未来的极端交通量,=GEV分布;=GEV参数的后验分布。本质上,后验预测分布通过将假定的数据分布与后验分布指定的所有可能参数值进行积分来解释参数不确定性。实际上,如果参数被认为是确定性的,那么公式(13)成为
这就是传统方法的情况,其中采用了参数的点估计。因此,与传统方法相比,贝叶斯方法可以将参数中固有的不确定性结合到预测中,并提供对未来结果的更可靠的估计。
在实践中,在方程式中的集成。公式(13)在给定后验分布的样本的情况下,很少进行分析。可以遵循下面描述的程序从后验预测分布中采样为对于i = 1:N(N =后验分布的样本大小),从给定来自后验分布的参数 的GEV分布生成大小为m的样本,即样本,,...,来自;重复步骤1直到我到达N并且获得的具有大小的样本会实现的从后验预测分布。
图3.路易斯安那州的I-10双跨大桥:(a)新的I-10双跨大桥(转载经许可Abu-Farsakh等作者许可。2014);(b)卡特里娜飓风破坏的原I-10双跨大桥(CS Cai图片)。
图4. I-10双跨桥梁的仪表:(a)仪表跨度的纵向剖面;(b)中跨钢跨的传感器布局(有交通流量);(c)中跨混凝土跨度的传感器布局(有交通流量);(d)M19码头(经阿布- Farsakh等作者许可转载。2014).
桥梁状况评估框架
桥梁状况评估的目的是评估桥梁的容量并检查桥梁是否可以安全地承载操作负荷。为了实现这一目标,图2中提出了一个框架来建议评估本研究中的桥梁状况。首先,关键位置的桥梁响应是由传感器测量。对于桥梁状态评估,应变响应可能是最重要的数据,因为它们反映了结构部件的安全储备(Ni等人。2012).其次,在信号处理时从传感器测量中提取桥的最大业务量LE,并且使用先前描述的贝叶斯方法来预测未来的极端业务量荷载效应。最后,将测量和预测的最大流量LE与响应包络进行比较,以确定桥的状况。
在拟议的框架中,开发了两个响应包络来评估两个层面的桥梁状况。第一个响应包络反映了桥设计要维持的实际负载(LL)容量,因此被称为设计LL容量包络。桥的流量LE不应超过此设计LL容量包络。否则,桥梁将受到严重损坏甚至在概
全文共16224字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[871]


