
英语原文共 10 页,剩余内容已隐藏,支付完成后下载完整资料
内容列表可在SciVerseScience Direct获得
欧洲业务研究杂志
期刊主页: www.elsevier.com/locate/ejor
O.R.的创新应用
混合负荷校车路径问题改进后的程序
Junhyuk Park a, Hyunchul Tae b, Byung-In Kim b,uArr;
a美国德克萨斯州木兰市信息技术研究所,邮编77354
b韩国波杭科技大学工业和管理工程系,波杭,京布790-784,
论文信息
论文史:
2010年11月3日收到,
2011年8月22日接受,
2011年8月30日可在线查阅
关键词:
组合优化
校车路线
混合负荷
车辆路径问题摘要
本文针对校车路径问题(SBRP),提出了一种混合负荷算法,并确定了其对所需车辆数的影响。SBRP试图为校车寻找最佳路线,每辆车在满足学生各种限制和需求的同时,将学生从家中运送到学校。允许混合乘车时,不同学校的学生可以同时乘坐同一辆公共汽车。尽管现实生活中的许多SBRP允许混合负荷,但只有少数研究考虑了这些情况。本文提出了一种新的混合负载改进算法,并与文献中唯一的混合负载改进算法进行了比较。为了比较算法的性能,激励其他研究者进一步研究,提出了基准问题。该算法在基准问题实例上的性能优于现有算法。它也已成功地应用于一些实际的SBRP,与目前的实践相比,可以减少所需的车辆数量。
copy; 2011 Elsevier B.V. 版权所有
- 导言
在本文中,我们提出了一种针对校车路由问题( SBRP)的混合负载算法,该算法旨在寻找一组车队(公共汽车)的最优路线。 每辆公共汽车必须从他们的家(或公共汽车站)接学生,并将他们转移到他们的学校, 同时满足各种限制,如车辆容量,学生在公共汽车上的最大允许乘坐时间,以及学校的时间窗口。 如果公共汽车专用于特定的学校,那么这个问题就变成了车辆路由问题( VRP);但在一般的SBRP中,一辆公共汽车可以为来自不同学校的学生服务;也就是说,一辆公共汽车可以访问几所学校。 关于SBRP的详细描述和相关文献的调查可以在Park and Kim (2010)中找到。
允许混合负荷的问题首先由Bodin and Berman (1979)讨论。 我们说“混合负荷是允许的”,如果来自不同学校的学生可以同时乘坐同一辆公共汽车。 当不允许混合荷载时,这个问题称为单荷载问题 (Bodin et al., 1983)。 关于SBRP的大多数研究不允许混合负荷(Park and Kim, 2010)。 然而,一些研究(Bodin and Berman, 1979; Bodin et al., 1983; Chen et al., 1988; Braca et al., 1997; Spada et al., 2005)讨论了与允许混合负荷有关的问题。 Bodin and Berman (1979)指出农村地区可以发生混合负荷。 Chen et al. (1988)指出单载假设可能是限制性的,可能需要过多的公共汽车给遥远地区的孩子。
uArr; 联系作者 电话 : 82542792371;传真: 82542792870。
电子邮件地址: bkim@postech.ac.kr (B.-I. Kim).
0377-2217/$ - 见前文 copy; 2011 爱思唯尔公司保留所有权利。内政部:10.1016/j.ejor.2011.08.022
Braca et al. (1997)声称,允许混合负荷可以增加灵活性和节省成本,但没有提供任何数字证据。 Braca et al. (1997)提到纽约市大部分地区允许混合负荷。 我们还发现,在我们最近的研究项目中,美国的许多学区允许混合负荷。
虽然有几篇论文简要地考虑了混合荷载问题,但只有Braca et al. (1997)实际上为混合负荷开发了一种算法。 他们修改了Bramel and Simchi-Levi (1995)的基于位置的启发式算法,该方法使用了一个简单的插入规则。 他们的算法通过迭代将最小代价站点及其对应的学校插入到一条路由中,直到不能再插入站点为止,依次构造路由。尽管他们的算法可以生成一组允许混合负载的路由,但是他们的研究并没有测量允许混合负载的效果。
而Braca et al. (1997)考虑混合负荷在他们的路线建设程序,我们在一个后改进程序的方法中考虑混合负荷。 首先,我们在不考虑混合负载的情况下生成一组路由,我们称之为单个负载计划。“单一负荷”一词被用作“混合负荷”的反义词(Bodin et al., 1983)。请注意,生成单个负载计划的任何算法都可以在我们的方法中使用。下一步,将混合负载改进算法应用于单一负载计划,使用简单的重定位操作将其转换为混合负载计划。
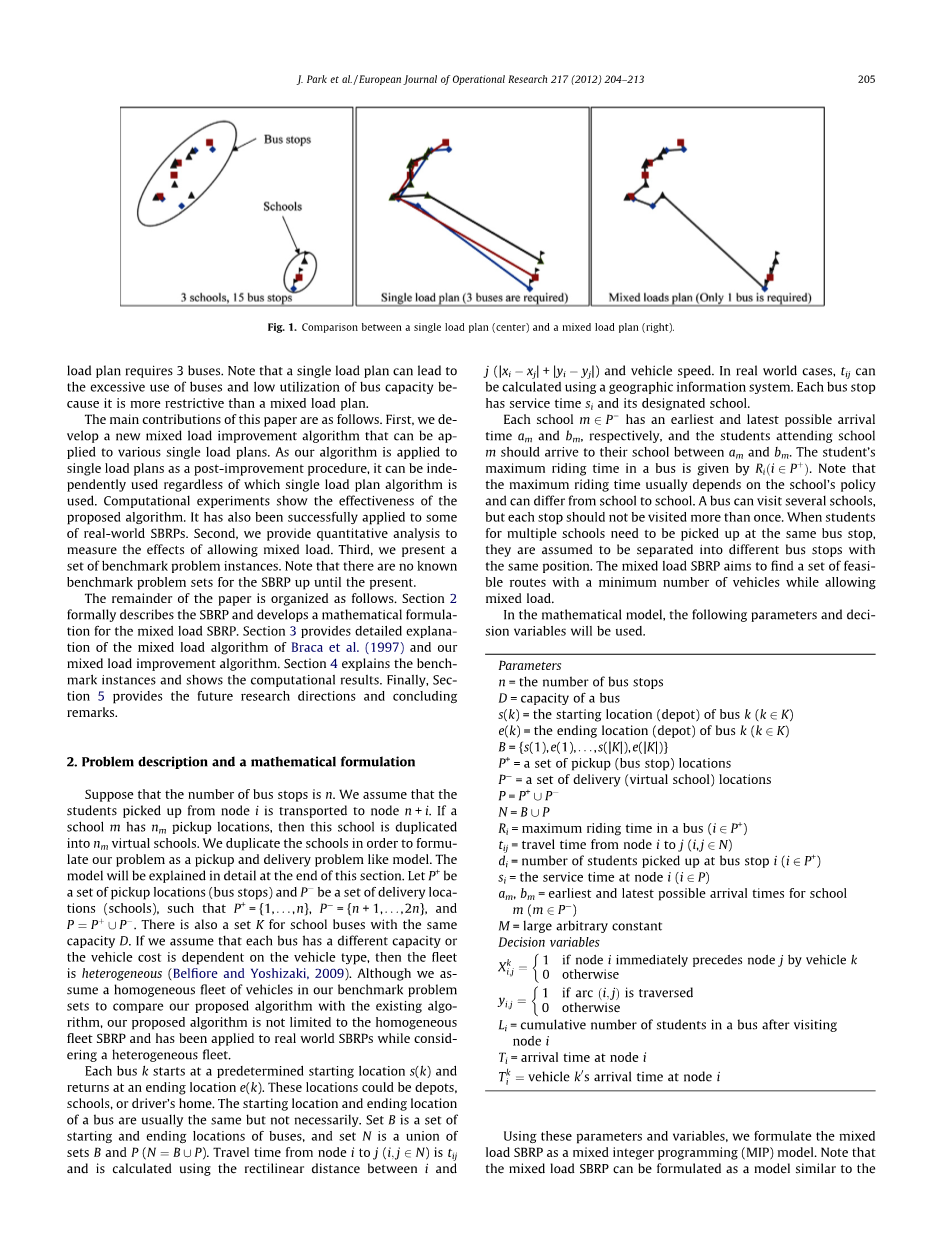
图1示出了单负荷计划和混合负荷计划之间的区别。我们生成了一个有3所学校和15个公共汽车站的例子,并用我们提出的算法进行了求解。在图中,混合负载计划只需要1个总线,而单总线负荷计划需要3辆公共汽车。 请注意,单个负载计划可能导致公交车的过度使用和公交车容量的低利用率,因为它比混合负载计划更具限制性。
205
. Park等人 /《欧洲运筹学杂志》217( 2012) 204-213
图 1. 单个负荷计划(中心)与混合负荷计划(右)的比较。
本文的主要贡献如下。首先,我们开发了一种新的混合负载改进算法, 可以应用于各种单负载计划。 由于我们的算法是作为后改进程序应用于单负荷计划,所以无论使用哪种单负荷计划算法,它都可以独立使用。 计算实验证明了该算法的有效性。 它也已成功地应用于一些现实世界的SBRP。第二,我们提供定量分析,以衡量允许混合负荷的影响。 第三,我们给出了一组基准问题实例。 请注意,到目前为止, SBRP还没有已知的基准问题集。
论文的其余部分组织如下。 第二节正式描述了SBRP,并为混合负载SBRP开发了一个数学公式。 第三节详细解释了Braca et al. (1997)的混合负载算法。和我们的混合负载改进算法。 第4节解释基准实例并显示计算结果。 最后,第五节提供了未来的研究方向和结论。
在现实世界中,可以使用地理信息系统计算tij。 每个公交站都有服务时间si及其指定学校。
每所学校misin;P—有可能最早、最晚到达的时间分别为AM和BM,上学的学生应在AM和BM之间到达他们的学校。 学生在公共汽车上的最大乘车时间是由Ri(iisin;P )给出的。 请注意,最大乘车时间通常取决于学校的政策,并可能因学校而异。 一辆公共汽车可以参观几所学校,但每一站不应超过一次。 当多所学校的学生需要在同一个公共汽车站被接走时,他们被假定被分成不同的公共汽车站,位置相同。 混合负载SBRP的目的是在允许混合负载的同时,寻找一组具有最小数量车辆的可行路线。
在数学模型中,将使用以下参数和决策变量。
问题描述和数学公式
假设公共汽车站的数目是n,我们假设从节点i接到的学生被传送到节点n i。 如果一个学校m有nm 的拾取位置,那么这个学校就被复制到nm 虚拟学校。 我们复制这些学校是为了把我们的问题形成一个类似于取货和送货问题的模型。模型将在本节末尾详细说明。 让 P 成为一组接送地点(公共汽车站)和 P—成为一组接送地点(学校),例如 P = {1,..., n}, P— = {n 1,...,2n},和P=P cup;P—同样容量的校车也有一组K。如果我们假设每辆公共汽车都有不同的容量,或者车辆成本取决于车辆类型,那么车队就是异质的(Belfiore and Yoshizaki, 2009) 虽然我们在基准问题集中假设一个同质车队,将我们提出的算法与现有的算法进行比较,但我们提出的算法并不局限于同质车队SBRP,并已应用于现实世界SBRP,同时考虑了异构车队。
参数
n=汽车站的数目
D=汽车的容量
s( k)=客车始发站K(kisin;K)
e( k)=公共汽车终点站K(kisin;K)
B = {s(1), e(1),..., s(|K|), e(|K|)}
P = 一组公共汽车站位置
P—= 一组虚拟学校地点
P=P cup;P—
N=Pcup;B
Ri =公共汽车的最长乘车时间 (iisin;P )
tij = 从节点i到节点j的行程时间 (i, jisin; N)
di =i站接学生人数 (i isin;P )
si =节点的服务时间(i isin; P)
am, bm = m学校最早和最晚可能到达时间 (m isin;P—)
M =大任意常数
决策变量
Xk={1 如果车辆k的节点i紧跟在节点j之前
i;j 0 否则
yi;j={1 如果超过弧(i,j)
0 否则
每个总线k在预定的起始位置s( k)开始,并在结束位置e( k)返回。这些地点可能是仓库、学校或司机之家。 总线的起始位置和结束位置通常是相同的,但不一定。 集合B是总线的起始和结束位置的集合,集合N是集合B和P(N=Pcup;B)的结合。 从节点i到j(i,jisin;N)的旅行时间 是tij,并使用i与j(|xi - xj| |yi - yj|)之间的直线距离计算车速。
Li
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[254514],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


