
英语原文共 20 页,剩余内容已隐藏,支付完成后下载完整资料
通过深度神经网络和树搜索精通围棋
David Silver1*, Aja Huang1*, Chris J. Maddison1, Arthur Guez1, Laurent Sifre1, George van den Driessche1, Julian Schrittwieser1, Ioannis Antonoglou1, Veda Panneershelvam1, Marc Lanctot1, Sander Dieleman1, Dominik Grewe1, John Nham2, Nal Kalchbrenner1, Ilya Sutskever2, Timothy Lillicrap1, Madeleine Leach1, Koray Kavukcuoglu1, Thore Graepelamp; Demis Hassabis1
围棋因其巨大的搜索空间以及评估棋盘位置和动作的难度,一直被视为人工智能经典游戏中最具有挑战性的游戏。在这里,我们介绍了一种新的计算机围棋方法,该方法使用“价值网络”评估董事会职位,并使用“策略网络”选择举动。这些深度神经网络是通过人类专家游戏中的有监督学习和自玩游戏中的强化学习的新颖组合来训练的。在没有任何前瞻搜索的情况下,神经网络以最先进的蒙特卡洛树搜索程序的级别下围棋,该程序可模拟成千上万的自玩游戏。我们还介绍了一种新的搜索算法,该算法将蒙特卡洛模拟与价值和策略网络相结合。使用此搜索算法,我们的程序AlphaGo相对于其他围棋程序获得了99.8%的获胜率,并以5:0击败了人类欧洲围棋冠军。这是计算机程序第一次在全尺寸的围棋击败人类职业棋手。
所有具有完美信息的游戏都具有最优价值函数v*(s),它确定了所有玩家在完美玩法下从每个棋盘位置或状态开始的游戏结果。这些游戏可以通过在搜索树中递归计算最佳值函数来解决,其中搜索树包含大约bd个可能的移动顺序,其中b是游戏的广度(每个位置的合法移动次数),d是游戏的深度(游戏长度)。在大型游戏中,例如国际象棋(basymp;35,dasymp;80)1尤其是围棋(basymp;250,dasymp;150)1,穷举搜索是不可行的2,3,但是有效搜索空间可以通过两个通用原则来减少。可以通过位置评估来减少搜索的深度:在状态s处截断搜索树,并用预测状态s的结果的近似值函数v(s)asymp;v*(s)替换s下的子树。这种方法导致了在国际象棋4,西洋跳棋5和奥赛罗6的超人表现,但是由于游戏的复杂性7,人们认为这种方法在围棋中是很难处理的。其次,可以通过从策略p(a|s)采样动作来减小搜索的广度,策略p(a|s)是位置s上可能移动a的概率分布。例如,通过从策略p采样两个玩家的长动作序列,蒙特卡洛推广8会搜索到最大深度而根本不分支。对此类部署进行平均可以提供有效的位置评估,在步步高8和Scrabble9中获得超人的表现,并在围棋中赢下较弱的业余水平比赛10。
蒙特卡洛树搜索(MCTS)11,12使用蒙特卡洛卷展栏来估计搜索树中每个状态的值。随着执行更多的仿真,搜索树变得更大,并且相关值变得更加准确。通过选择具有较高值的子级,随着时间的推移,用于选择搜索过程中的操作的策略也会得到改进。渐近地,该策略收敛到最优玩法,并且评估收敛到最优值函数12。当前最强大的围棋程序基于MCTS,并经过培训以预测人类专家动作的策略得到增强13。这些策略用于将搜索范围缩小到一堆高概率动作,并在推出期间对动作进行采样。这种方法取得了不错的业余成绩13-15。但是,以前的工作仅限于基于输入特征的线性组合的浅层策略13-15或价值函数16。
最近,深度卷积神经网络在视觉领域取得了前所未有的性能:例如图像分类17,面部识别18和玩Atari游戏19。他们使用许多神经元层,每层神经元排列在重叠的图块中,以构造越来越抽象的局部图像表示20。我们为围棋采用了类似的架构。我们以19times;19的图像传递木板位置,并使用卷积层构造该位置的表示。我们使用这些神经网络来减少搜索树的有效深度和广度:使用价值网络评估职位,并使用策略网络对行动进行抽样。
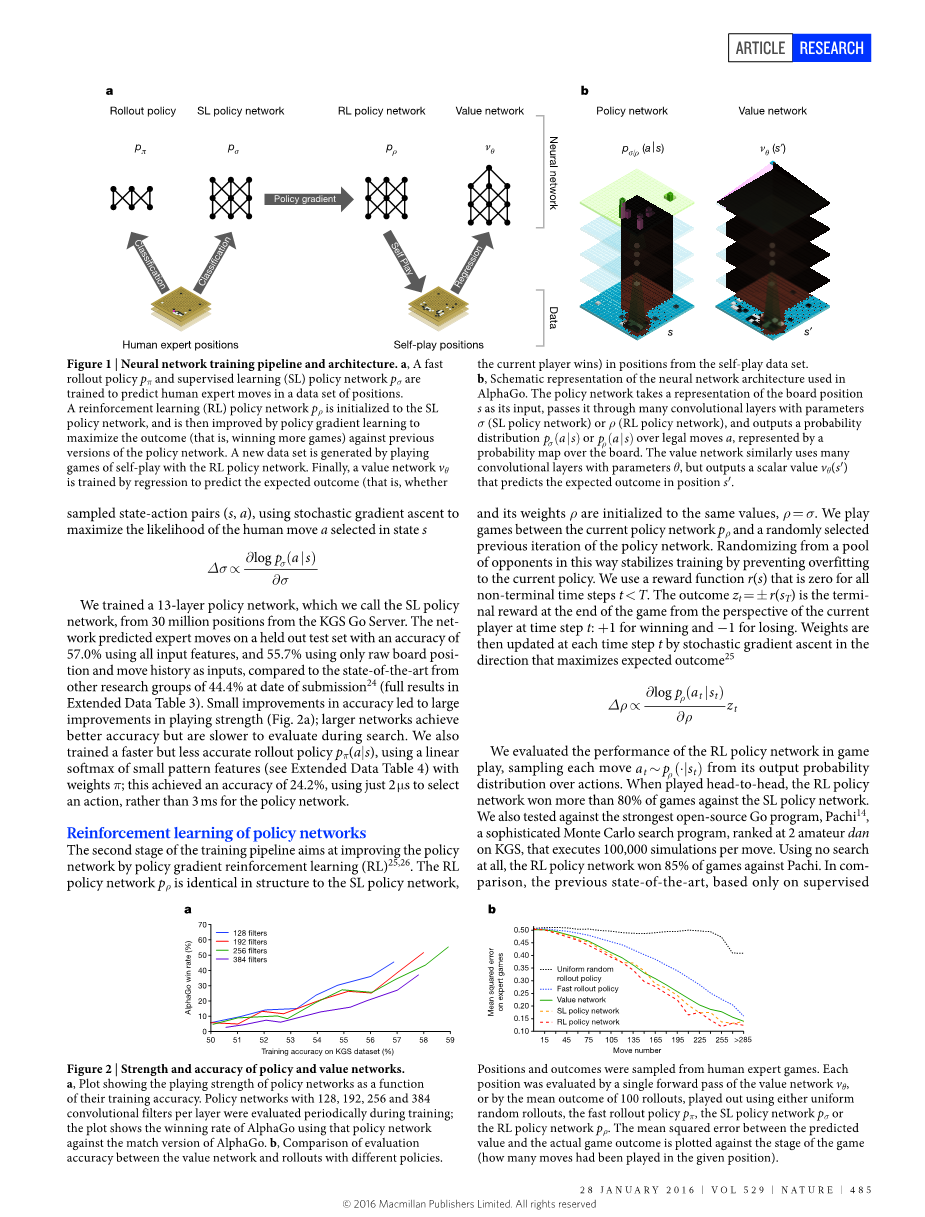
我们使用由机器学习的多个阶段组成的管道来训练神经网络(图1)。我们首先直接从专家的举动中训练监督学习(SL)策略网络psigma;。这样可以提供快速,有效的学习更新,并具有即时反馈和高质量的渐变效果。与先前的工作类似13,15,我们还训练了快速策略ppi;,可以在部署过程中快速采样操作。接下来,我们训练强化学习(RL)策略网络pp,它通过优化自玩游戏的最终结果来改进SL策略网络。这将策略调整为赢得比赛的正确目标,而不是最大化预测准确性。最后,我们训练了一个价值网络vtheta;,它预测RL策略网络对自己的游戏赢家。我们的计划AlphaGo有效地将策略和价值网络与MCTS结合在一起。
策略网络的监督学习
在培训流程的第一阶段,我们基于先前的工作,使用监督学习预测围棋游戏中的专家动作13,21-24。SL策略网络psigma;(a|s)在权重为sigma;的卷积层与整流器非线性之间交替。最终的软最大层在所有合法移动a上输出概率分布。策略网络的输入s是板状态的简单表示。使用随机梯度上升对策略网络进行随机抽样的状态-动作对(s,a)的训练,以最大程度地提高人类在状态s中移动选定状态的可能性
我们从KGS Go服务器的3000万个职位中训练了一个13层策略网络,我们将其称为SL策略网络。网络预测专家将使用所有输入功能在保留的测试集上进行移动,与最新技术相比,其准确度为57.0%,仅使用原始木板位置和移动历史作为输入的准确性为55.7%在提交之日,其他研究小组的研究成果占44.4%24。准确性的微小提高导致比赛强度的大幅提高(图2a);较大的网络可获得更高的准确性,但在搜索过程中评估速度较慢。我们还使用权重为pi;的小图案特征的线性softmax训练了更快但不太准确的部署策略ppi;(a|s)。仅使用2mu;s来选择一个动作,而不是使用3ms的策略网络,就达到了24.2%的精度。
图1|神经网络训练流水线和架构。a,对快速推出策略ppi;和监督学习(SL)策略网络psigma;进行了训练,以预测人类专家在位置数据集中的移动。强化学习(RL)策略网络prho;初始化为SL策略网络,然后通过策略梯度学习进行改进,以最大程度地提高策略网络先前版本的结果(即赢得更多游戏)。通过使用RL策略网络进行自玩游戏来生成新的数据集。最后,通过回归训练价值网络vtheta;,以预测自玩数据集中的位置的预期结果(即,当前玩家是否获胜)。b,AlphaGo中使用的神经网络架构的示意图。策略网络将代表板位置s的表示作为其输入,使其通过具有参数sigma;(SL策略网络)或rho;(RL策略网络)的许多卷积层,并输出概率分布psigma;(a|s)或prho;(a|s)超过合法移动量a,由板上的概率图表示。价值网络类似地使用许多带有参数theta;的卷积层,但是输出一个标量值vtheta;(s),该标量值预测位置s上的预期结果。
策略网络强化学习
培训流程的第二阶段旨在通过策略梯度强化学习(RL)25,26改进策略网络。RL策略网络prho;在结构上与SL策略网络相同,其权重rho;初始化为相同的值rho;=sigma;。我们在当前策略网络prho;和策略网络的随机选择的先前迭代之间进行游戏。通过这种方式,从反对者群体中随机分组,可以通过防止过度适应当前策略来稳定训练。对于所有非终端时间步长tlt;T,我们使用的奖励函数r(s)为零。从当前玩家的角度来看,结果zt=plusmn;r(sT)是游戏结束时的最终奖励,时间步长t: 1表示获胜,-1表示失败。然后,在每个时间步长t处,通过在最大预期结果的方向上进行随机梯度上升来更新权重25
我们评估了RL策略网络在游戏中的性能,并根据其在动作上的输出概率分布,以at~prho;(·|st)采样了每一步。当面对面比赛时,RL策略网络在与SL策略网络的对抗中赢得了80%以上的比赛。我们还针对最强大的开源围棋程序Pachi14,一个复杂的蒙特卡洛搜索程序进行了测试,该程序KGS排名为业余2段,每步执行100,000个模拟。完全不使用搜索,RL策略网络赢得了针对Pachi的85%的比赛。 相比之下,以前的最新技术仅基于对卷积网络的监督学习,在与Pachi的对抗中赢得了11%的比赛23,而在稍弱的程序Fuego24中则赢得了12%的比赛。
图2|策略和价值网络的实力和准确性.a,该图显示了根据其培训准确性而定的策略网络的运行强度。在训练期间定期评估每层具有128、192、256和384个卷积过滤器的策略网络;该图显示了使用该策略网络的AlphaGo与匹配版本的AlphaGo的获胜率。b,价值网络与采用不同策略的推广之间评估准确性的比较。位置和结果是从人类专家游戏中抽取的。每个位置均通过价值网络vtheta;的单个前向传递或通过使用均匀随机部署,快速部署策略ppi;,SL策略网络psigma;或RL策略网络prho;进行的100个部署的平均结果进行评估。相对于游戏阶段(在给定位置进行了多少步),绘制了预测值和实际游戏结果之间的均方误差。
图3|在AlphaGo中进行蒙特卡洛树搜索。a,每次模拟都通过选择具有最大作用值Q的边加上依赖于该边的已存储先验概率P的奖励u(P)来遍历树。b,可以扩展叶节点;策略网络psigma;对新节点进行一次处理,并且将每个操作的输出概率存储为先验概率P。c,在模拟结束时,以两种方式评估叶节点:使用值网络vtheta;;并通过快速推广策略ppi;将推广运行到游戏结束,然后使用函数r计算获胜者。d,更新动作值Q以跟踪该动作下方子树中所有评估值r(·)和vtheta;(·)的平均值。
价值网络的强化学习
训练流程的最后阶段着重于位置评估,即评估价值函数vp(s),该值函数对两个玩家都使用策略p来预测游戏位置s的结果28-30。
理想情况下,我们想知道完美执行v*(s)下的最优值函数;实际上,我们改用RL策略网络prho;估算最强策略的价值函数vrho;p。我们使用具有权重theta;的值网络vtheta;(s)近似值函数,其中vtheta;(s)asymp;vprho;(s)asymp;v⁎(s)。该神经网络具有与策略网络类似的体系结构,但是输出单个预测而不是概率能力分布。我们利用状态梯度对(s,z)的回归值来训练价值网络的权重,使用随机梯度下降法将预测值vtheta;(s)与相应结果z之间的均方误差(MSE)最小化。
从包含完整游戏的数据中预测游戏结果的幼稚方法会导致过拟合。问题在于,连续位置之间存在很强的相关性,相差仅一石之遥,但是回归目标在整个游戏中都是相同的。当以这种方式在KGS数据集上进行训练时,价值网络会记住游戏结果,而不是将其推广到新位置,从而使测试集的最小MSE为0.37,而训练集的最小MSE为0.39。为了缓解这个问题,我们生成了一个新的自我游戏数据集,该数据集由3000万个不同的位置组成,每个位置都是从独立游戏中采样的。每个游戏都在RL策略网络与其自身之间进行,直到游戏终止。在此数据集上进行
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[259962],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


