
英语原文共 13 页,剩余内容已隐藏,支付完成后下载完整资料
使用叶片形状的植物识别方法——一种图像计数方法
1、介绍
植物识别不仅仅是植物学家和植物生态学家的工作,各行各业都需要。从景观设计师,树木栽培师,草药医生,保护主义者和生物学家等专业人士,到生态旅游者,徒步旅行者,公园游客和自然爱好者等一般公众。然而,植物识别并不是一件容易的事,需要专门的知识和植物学和植物系统学的深入培训。如今,随着信息技术的蓬勃发展,人们期待着拥有一个自动化的工厂识别系统,以便用户可以通过移动设备的内置摄像头拍摄工厂的现场,并将其提供给预先安装的识别程序,以找出可能的物种的信息。
在植物的器官中,例如花粉,果实,茎和树皮,叶子通常用于植物鉴定,因为其特征更具普遍性和持久性。虽然这些字符适用于计算机系统,但对叶子的准确识别仍然存在挑战:(1)叶子可以在任意姿势下成像,其部分可以清晰表达。 例如,其叶柄和叶片的相对姿态可以在不同的图像中改变。(2)由于形态变异,叶片的形状具有较大的类内差异和类间相似性。例如,一些植物物种具有相似的整体形状但不同的边缘细节。忽略这一重要事实,现有方法在实现良好性能方面存在困难。(3)复叶尤其难以识别,并且已有的专为识别简单叶子而设计的算法很难直接应用。这是因为复叶的变异不仅仅是由于叶片的形态差异引起的,也可以通过改变数字和排列。
在本文中,我们提出了一种新的算法,可以准确识别简单叶和复叶。在受到植物系统强度启发的特定项目中,我们提出了一种新颖的特征,它不仅能够稳定地进行接合处和平面内旋转,还能够比现有方法更好地捕获生物信息(整体形状,边缘类型,几何形状和排列)。此外,我们发现这些特征具有不同物种的叶子在不同数据集中共有的模式。我们使用学习方法发现这种形状模式,它们在某种程度上在植物系统学中像分类群一样--每个形状图案描述了许多物种的共同特征,并且所有图案一起形成识别的辨别原则。最后,与叶子个体中匹配形状特征的现有方法不同,我们总结了用于表示整片叶子这种模式的数量,并将得到的计数作为分类的描述符。在五个数据集上进行的实验表明,所提出的方法在识别准确性,效率和存储方面显着优于现有技术需求。
本文的其余部分安排如下:第2节介绍相关的作品,第3节介绍最相关的方法并分析其在实际情况下的问题。第4节讲述了我们提出的方法,并在第5和第6节与现有技术方法相比测试其性能。最后,我们在第7节通过得出结论并讨论未来的工作来结束本文。
2、相关工作
叶片图像识别的研究工作最近开始吸引计算机视觉和相关领域。这类工作的主要内容包括测量几何特性。例如,吴等人使用纵横比,矩形和窄因子作为特性,并采用神经网络作为分类器。他们在10种数据集上实现了高达90.3%的识别率。Pahalawatta等使用了一组不同的特性–-茎与茎之间的比率和紧密度。这些方法的一个常见缺点是几何特性难以在不完美的测量下精确提取,并且它们之间的加权也是有问题的。因此,它们无法区分大量物种。
另一项工作是利用形状描述符。Soderkvist 结合曲率尺度空间,傅里叶描述符和Hu的时刻构建树状结构分类系统,并在包括15种物种的瑞典数据集上进行测试。凌等人提出了一种新颖的形状描述符,称为 Inner-Distance Shape Context(IDSC),据称它表现得更好。它通过在IDSC特性之间建立点-点匹配来测量两个叶子之间的相似性。该方法被进一步用于开发工作系统,直到那时叶子分类才变得容易在现实生活中使用。虽然它们在简单的叶片识别方面取得了令人印象深刻的成果,但它们的方法在锯齿状叶片和复叶片上效果不佳,这将在下文第3节中进行解释。最近,一些研究人员意识到不适合使用形状匹配进行叶片图像识别,并提出使用曲率直方图和线性子空间。然而,这些方法或者需要对叶柄进行特殊处理,而且不能像我们的那样获得好的结果,将在下文第5节中解释。
使用花朵进行植物识别也发现了一些成果。他们的方法结合了许多视觉特性,并且能够对102个类别进行分类,识别率高达72.8%。然而,使用叶子仍然具有第1节所述的优点,我们认为,在植物鉴定系统中利用花卉和潜在的其他器官信息互补是一种趋势。
3、评论IDSC特性
我们评论以下作品,因为它们与我们的成果最相关。
3.1.Shape context(SC)
Belongie等提出了一种称为SC的形状描述符,它通过将所有需处理的点的相对距离和角度量化为2D直方图来计算每个轮廓点。换句话说,每个轮廓点的形状特性在于整个2D直方图中的上下文。因此将匹配两个不同的形状减少为匹配两组这样的直方图,这可以通过使用二分图匹配来完成,最近邻居法或动态编程。
3.2.Inner-distance shape context(IDSC)
在许多情况下,叶片形状的不同部分可以有关联,例如,叶柄和同一片叶子的叶片的相对形态可以在不同的图像中改变。这种关联对计算出的SC有显著的变化。为了获得接合处的不变性,Ling等人用“内距离”和“内角”代替了欧氏距离和相对角度。据报道IDSC得到的2D直方图在Swedish和Smithsonian数据集中叶片识别的表现优于许多其他描述符。
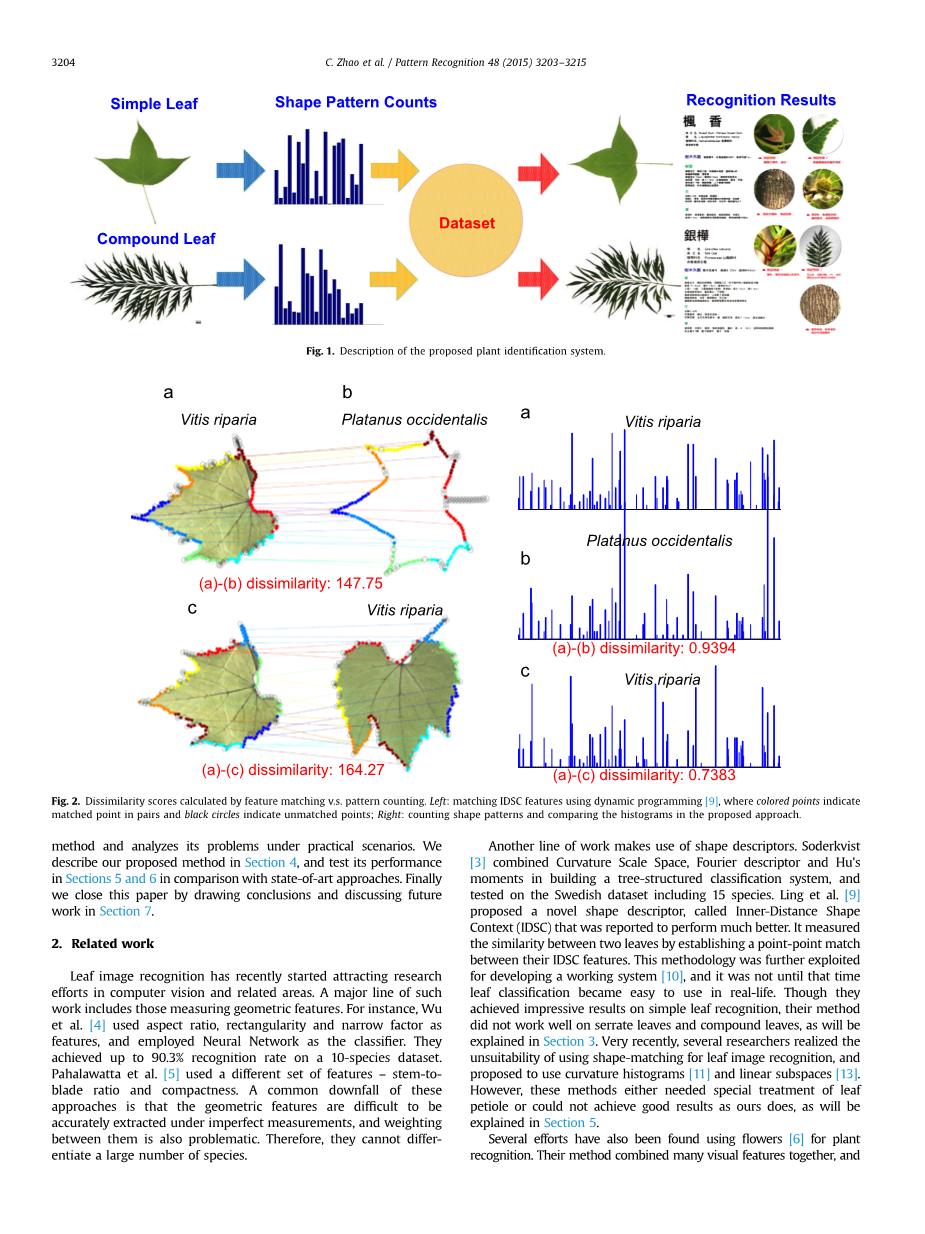
然而,我们在研究中发现:(1)IDSC不能很好地模拟叶子形状的局部细节,因为它是以混合方式从所有轮廓点计算的,全局信息在计算中占主导地位。因此,两个具有相似全局形状但不同局部细节的不同叶片往往被错误地分类为同一物种。(2)通用形状分类方法的点匹配框架对于锯齿状叶和复叶都不能很好地工作,因为它们的局部细节难以成对匹配,并且对于同一物种的叶子,相异性得分可能比不同的那些更高。示例图2(左)中大多数不匹配的点(黑色圆圈)出现在包含丰富的边缘类型信息的锯齿周围。(3)点匹配框架对于大型数据集的实时分类也是无效的,我们观察到[9,10] 在识别准确性和效率之间做了妥协。
4、提出的方法
植物学家如何对树叶进行分类?我们从植物系统学中学习到植物学家使用独立的“键”对叶进行分类的重要原则——简单叶的总体形状、顶角/底角和边缘类型,以及复合叶小叶的形状和排列。此外,他们使用这些键将叶子分类为许多分类群--每个分类群都表征了不同物种叶子常见的特征,所有分类群共同构成了分类的判别规则。
遵循上述原则,我们在本节中介绍一种使用形状模式的叶识别方法。这些模式在某种程度上可以模拟识别键--每种模式都表征了各种物种中存在的共同特征,所有模式都具有高度的辨别力。在具体的细节中,我们首先提出了基于IDSC理念的Independent-IDSC(I-IDSC)特性--它使用内距和内角,因此使接合处和旋转处的特性不变。然而,I-IDSC不是以混合方式计算全局和局部信息,而是独立地计算它们,以便可以单独检查叶形的不同方面。此外,我们发现从不同植物物种中提取的I-IDSC特征的集合可以具有共同的形状模式,并且我们通过在培养集上学习来发现这些模式。最后,我们不是像传统方法那样在叶子个体上匹配特征,而是总结整个叶子上的形状模式的数量,并将得到的计数作为分类的描述符。
与传统方法相比,我们的优势是三方面的:(1)它区分具有相似整体形状但边缘和副边不同的叶子,反之亦然; (2)它准确地分类简单叶和复叶; (3)它只保留最具辨别力的信息,因此非常快且存储便宜。
4.1.I-IDSC特性
提出的I-IDSC特性的计算涉及两个部分:高斯形状金字塔和依赖于尺度的上下文。我们首先假设已经提取了研究中叶子的轮廓,并且由n个点的有序序列表示:[x1,y1,...,xn,yn]。
4.2.高斯形状金字塔
我们通过将叶轮廓的x和y坐标与具有逐渐增加的sigma;的高斯滤波器N(0,sigma;)卷积来构造金字塔。通过这样做,我们在不同的尺度上保持不同级别的细节。 在具体情况下,我们使用3个尺度--在最粗糙的尺度只捕获整体形状;在中等尺度上,单叶的锯齿状排列和复叶的小叶状排列都得到反映;而在最佳尺度上,所有边距和嫩叶细节都被保留,如图4所示。但是,到此步骤,详细信息仍取决于全局形状。我们进一步采用与尺度相关的上下文以最小化这种依赖性。
4.3.依赖于尺度的上下文
在计算I-IDSC特性时,我们定义了环境轮廓点的一部分作为所涉及的相邻点的集合,如图4由绿色曲线连接的点所示。我们根据尺度调整上下文,并在不同尺度上使用不同大小的上下文。计算一个点的I-IDSC时(图4中用红色标记表示)在最粗糙的尺度上,我们将所有n-1个需处理的点作为环境;虽然在最佳范围内,我们只占用了几个邻域(就内部距离而言)。
形式上,S标度处轮廓点P的I-IDSC特性Xs通过以下公式计算:
式中k为角距离文件中的指数,p、q为点,q-p按内距、内角计算。而Cs(p)是包含Ns=n/tau;s-1的环境。围绕p点的邻域(就内部距离而言)随着s增加1,Ns 降低tau;。这样以来,我们逐渐在细的尺度上定位环境,以便这样的局部信息--反映简单叶子的边缘细节和复合叶子的形状--可以独立于它们的整体形状。如从右下角图4可以看出,如果tau;(本文通篇tau;=4)选择得当,小叶顶端的特征只反映了小叶的形状,这有利于比较复合叶。
事实上,Felzenszwalb等人从粗到细研究了形状分类的概念。世卫组织提出了一个形状树模型来计算两个通用形状之间的相似性。然而,他们的方法仍然是一种点匹配方法,它不能像我们的方法一样对叶子进行分类,如第5节所示。此外,[10]中发现它太慢,无法在实时系统中应用。相比之下,我们采用这种想法来独立地捕获叶子的不同方面,就像在植物系统学中一样。
4.4.常见的形状模式
我们计算I-IDSC的方式反映了这些特性的重要性质--它具有共享效应。从不同叶子提取的特征可以具有一定规模的共同模式。只要叶子具有相似的全局形状或局部细节,即使它们来自不同的大陆,它也是成立的。这是因为计算I-IDSC特性的环境非常相似,即使如图6它们位于不同的叶子上。
这种共享效应已在一般对象识别中发现,并也在植物系统学中观察到:(1)植物学家使用了几种识别键,例如:顶点或基部的形状,用于分类不同的叶子。 每个识别键将叶子分成几个类别,例如:锐尖的顶部或心形基底等。(2)不同物种的叶子,如果用特定的识别键测量,可能最终属于同一类别。受这些事实的启发,我们制定了以下合作法表示的假设:
假设:I-IDSC特征Xs的尺度s可以写成字典中只有几个形状模式的线性组合这是不同的共享种类。
Xs=Dsalpha;s
s.t.||alpha;s||0le; L (1)
其中Ds是刻度s的形状模式的字典矩阵,Ds的每列是形状模式; alpha;s是系数向量,ℓ0拟范数由||alpha;||0=#{alpha;(i)ne;0}定义。L表示一个合理小常数和等式。I-IDSC特性总是“触发”不超过字典中L个形状模式。这个想法类似于植物系统学,叶子只能属于少数几个(理想情况下为一种)由识别键定义的类别(例如,尖锐的尖端)。
注意,对于任何给定的x,一旦Ds已知,alpha;s可通过求解convex relaxed optimization problem(文献中称为 Basis Pursuit)来计算:
式中,ℓ1-范数||alpha;||1=Sigma;i|alpha;(i)|是ℓ0-范数的最紧凸松弛,并且已经在[32,33]中证明(2)在相当宽泛的条件下得到最优解。在实践中,观测Xs中存在噪声,因此我们使用(2)的基础追踪去噪(BPDN)版本,其公式如下:
这里,lambda;是平衡观测噪声和稀疏度的加权因子。
为了理解所学形状模式的结构,我们提供了问题的几何解释。设p为plusmn;Ds柱凸组合所形成的对称凸多面体。然后,根据1-范数最小化的几何关系,求解(2)等于求出最小的标度因子delta;,使标度多面体delta;p与输入数据xs接触,得到的delta;为最优alpha;s的1-范数。图7给出了一个图解,它表明:(1)形状模式的正负倍数在高维特征空间中形成了一个凸多面体,(2)对于给定的 I-IDSC特性,通过解式(2)找到其表示,基本上确定了它落在多面体的哪
全文共11421字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[2740]
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


