
英语原文共 7 页,剩余内容已隐藏,支付完成后下载完整资料
社会群体中行人的步行行为和其对于人群动力学的影响
摘要: 人的群体运动主要是由基于行人之间的局部相互作用的自组织过程驱动的。虽然大多数研究人群的行为只考虑孤立的个人之间的相互作用,结果表明,人群中多达70%的人实际上是作为群体在移动的,如朋友,夫妻,或走在一起的家庭人员。这些群体构成了中等规模(一定规模)的聚集结构,并且其对人群动态的影响仍然是未知的。在这项工作中,我们分析了在自然条件下的约1500个行人人群的运动,结果表明了群体成员之间的社会影响产生了能够影响人群动态的典型群体行走模式。在低密度时,组成员倾向于并排走,形成一条垂直于行走方向的线。随着密度的增加,情况发生了改变,直线行走的趋势变成了向前弯的形态,把它变成一个“V”型模式。这些行为的空间模式可以很好地被一个基于群体成员之间的社会关系交流的模型来进行描述。我们的实验结果表明,“V”字形的行走模式有利于本群体内的社会互动,但由于不是”空气动力学“的形状模式,从而降低了流通性。因此,当人群密度增加时,群体的组织方式是由如何权衡在走得更快和促进社会人群之间的交流而从产生的。这些见解表明,人群动态行为不仅取决于由其他行人和环境而产生的物理约束,同时也凸显了人之间的交际,以及人在社会中的相互影响而产生的作用。
介绍:
人群动力学的研究最近证实了在许多研究领域[1,2,3,4,5]都有极大的应用。为了开发可靠的预测模型用于城市基础设施的设计,交通管理或在混乱情况和疏散过程中人群的安全,有必要去了解局部的互动规律所引起的人群动态的连锁反应。
虽然有很多已知的关于人群运动的意外的物理特性,如在狭小的出口处(瓶颈)处出现自组织[6,7],在相对行走的人群中出现的离散现象[8,9,10],或在高密度人群中的无规则运动[11,12],令人惊讶的是,出现以上情况时在人群中的行人把社会互动(人之间的交流)很大程度的遗忘了。事实上,绝大多数现有的研究调查都是把人群作为一个孤立的个体,每个个体都有一个自己期望的速度和运动方向,参考文献[9,10,13,14]。然而在现实中,现象表明多数行人其实并不是单独行走,而是作为一个群组的单位进行移动[ 15,16,17 ]。正如我们将在这篇文章中展示的那样,在商业街步行中多达70%的行人是以组为单位进行运动的。早期观察表明,由2到四个成员组成的组是最常见的,而由五和更大数量的群组是比较少见的。此外,组大小分布满足泊松分布[ 17 ]。
然而,以我们目前掌握的知识来说,行人群体的运动特征到目前为止还没有进行实证性的研究。运动中的群组成员是如何相互作用,是如何与其他行人和其他群体基本进行互动仍是未知的。它也需要去研究空间群组的自组织现象以及空间格局如何影响人群的动态组织。这对于规划行人行为能力(facility),大规模人群事件和疏散层面将有着重大的意义。
我们注意到,在这里所使用词“group“是基于其社会学意义的[18],这不仅指的是刚好走到一起而靠近彼此的行人,而且也指那些有社会层面上有关系的人从而有意走在一起,如朋友或家庭成员之间。特别是,人之间持续时间的互动和沟通能够区分是否是一个偶然的聚合。
在这项工作中,我们分析了社会群体中行人的自组织现象以及对复杂的人群动态行为的影响。为此,我们通过公共领域的视频记录来收集运动的行人群体的相关数据。在低和中等密度条件下观察,可以分别将人群命名为A和B。我们分析了A群体中人数为N_A=260的人数和B群体中N_B=1093个群体的人口并由2到4个成员组成一组(see Material amp; Methods)的行为。根据我们观察到的资料,我们开发了一个基于个人的行人行为模型。该模型描述了一个人如何与其他组的成员和不同类别中的组的行人的相互作用。通过数值模拟,结果表明了,该模型能很好地预测了以以往经验观察收集到的步行模式的出现,以及预测了行人群体构成的人群自组织的一个重要要素。
根据我们的实证分析,在人群A和人群B中,行人走到一组一组的比例分别是55%和70%,即高于单独行走的行人比例。如图1所示,在群体A中的群体大小服从零截尾(zero-truncated的)泊松分布(P = 0.06;基于x^2的基础上测试),与之前的观察一致[ 15,19 ]。在人群B中,基于同样的观察趋势,但单人行走的比例比预期的泊松分布比率要低,而群组中人数大小为2的比例要大于预期(Plt;0.01)。群体A和B之间的这种差异可能是由于观察者处于不同的观察环境而导致的:群体A是在一个工作日的下午观察,而B种群是在周六有名的商业步行街进行观察的,而在步行街观察能有一个更高的趋势观察到人们和朋友一起出行散心。社会环境的影响在过去已经被观察到了[15,19 ],即在休闲区域如购物中心或公共海滩则有更高的频率形成群组。过去的研究表明,被观察的群体大小分布可以通过假设个体在每个单位时间内都有一定的几率可以独立加入和离开一个群组,并且在失去一个成员的速度对于群体规模来说是成比例变化的来进行解释。根据分析计算,这种机制可以产生所观测到的分布[ 15 ]。
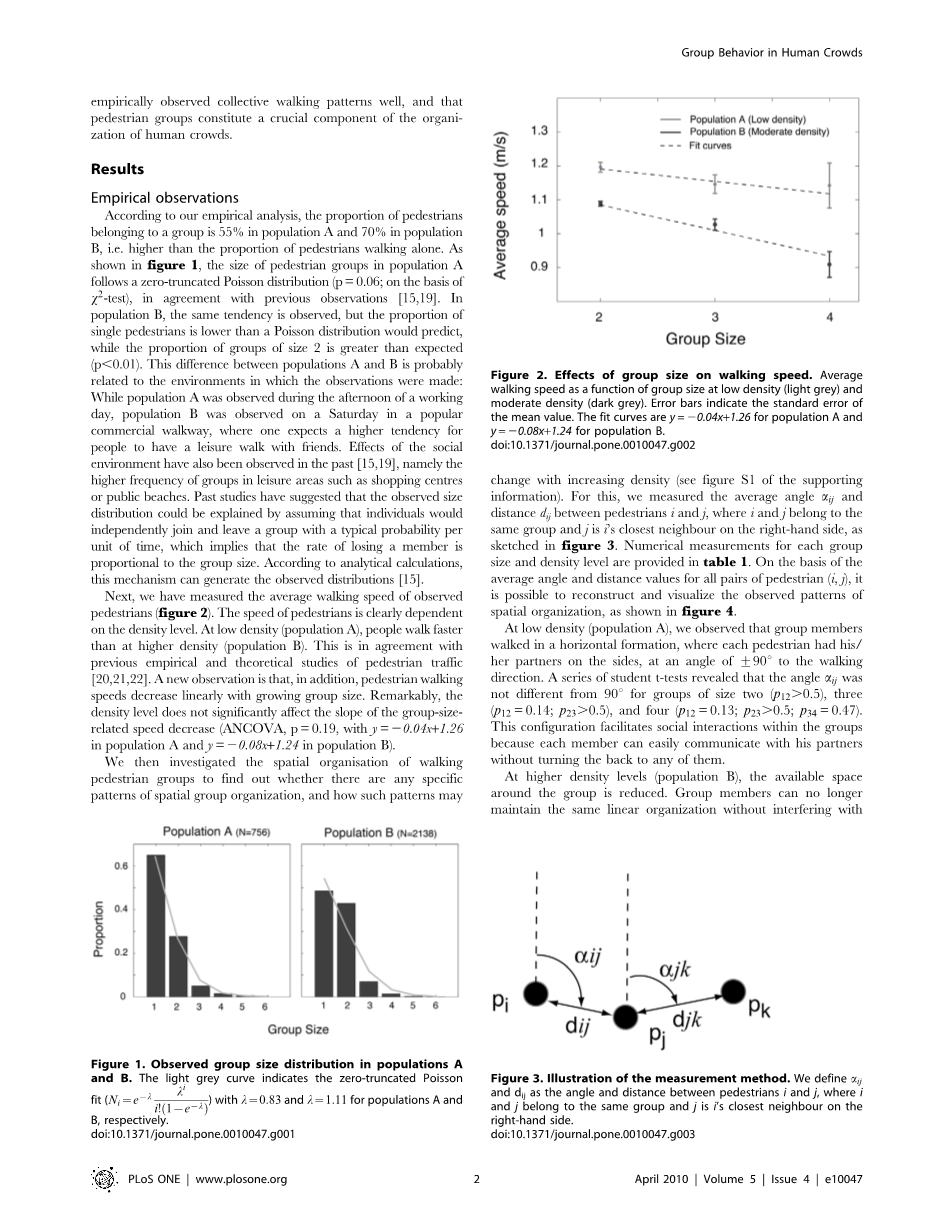
接下来,我们测量了所观察的行人的平均行走速度(如图2)。行人的速度显然是依赖于密度的水平。在低密度情况下(如人群A),人们行走速度快于在高密度的情况(如人群B)。这与先前观察到的和行人行走规则的理论上的研究[20,21,22]是一致的。一个新的观测表明,不仅如此,行人步行速度随着群体大小的增长呈线性下降。值得注意的是,密度水平并不是影响群组中行人速度(group-size-related)斜率减小最主要的影响因素。协方差模型中, p=0.19时人群A的方程为 y=20.04x 1.26 , 人群B满足的方程为 y=20.08x 1.24。
然后我们研究了行人群体的空间组织以找出是否有任何特定的空间组织模式,以及这些模式如何随密度的变化而发生变化(参见图S1所表明的信息)。为此,我们测得了行人i和j之间的平均角度 和距离 ,其中i和j属于同一组并且J是I右手边最临近的个体,如图3所示。每个组的大小和密度水平的测量数值如表1所示。基于对所有成对的行人(I,j)所具有的平均角度和距离的值,,它可以重建并可视化空间组织的观察模式,如图4所示。这种排列有利于群体之间的社会交往,因为每个成员可以在不用背对其伙伴的情况下很容易地与之进行交流。
在高密度人群中(人群B),群组周围可用空间被减少了。组成员在没有其他组成员的干扰下可以不再保持相同的线性组织方式。如表1中所示,组成员之间的平均距离事实上在减少。此外,群组组成大小的改变:在组规模为3人时,我们观察到处于中间的行人(P 2)趋向于往后站,所以行人P 1和P 3就更接近彼此了。这就形成了一个“V”字型的形状,1、2之间的角度就超过了90度,2、3之间的角度小于90度。同理,对于4个人组成的群体,行人P2和P3趋向于往后移,形成“U”字型。因此,在低密度时观察到的水平行走的形状在密度水平增加时产生弯曲,并允许该组占据一个较小的区域。然而,令人惊讶的是弯曲的方向与人向前行走的方向一致,而不是向后移动,就像预期的灵活的结构对反向流进行相反的移动。这表明,这种结构是可以乐观地创建和维护,以支持某些特定的功能(如更好的沟通)。
为了更好地理解上述的实证结果,我们扩展了现有的行人行为模型以包括行走的行人之间的社会相互作用力。对于这一点,我们依靠社会力模型的实验规范,其必须在之前的工作中进行实验校准和验证[ 9 ]。基本的建模概念表明,行人I的运动可以用反应行人以特定的期望速度朝一个给定的预期方向移动时的驱动力的合力来描述,排斥力表示与其他独立的行人j之间的相互作用力,反映了与边界间的排斥作用力,如墙壁或街上的障碍物(见Material amp; Methods表述这些数学规范上的相互作用力)。在这一节中,我们提出了一个新的相互作用力来描述行人i与其他组成员间的相互作用力。因此,完整的运动方程表示如下所示:
我们假设观察到的人群自组织模式是由他们各自的成员间彼此沟通的愿望而产生的。因此,个体不断调整自己的位置以方便彼此的交流,同时尽量避免与本小组成员以及其他组成员间的碰撞。特别是,已经证实的是视线方向和目光接触是组间通信的本质特征,并且有助于从其他人的反应中得到反馈[ 23、24、25]。因此,我们引入了一个视觉领域概念作为我们的行人仿真模型的一个重要组成部分。
模拟结果:
上述模型的计算机模拟以反应人群A和B的经验条件(empirical condition)的方式被执行(见Material amp; Methods)。对于所观察到的数据,我们测量了每个对行人的平均角度和距离,并研究了相关的组织模式。模拟群体是由共同的(collective)与以往非常匹配的步行模式而形成的(参见图4)。特别是,一系列Student t-tests显示不同角度分布的观察和预测结果之间无显著性差异(see the table S1 in Supporting information)。该小组的空间格局主要受参数 的影响,代表群体成员之间的社会互动的力(图6)。当设置为 = 0,组成员只整合成一个整体没有通信规则,往往会形成一个“空气动力学”上的逆V型结构。相反,对于现实的 = 4,群体形成了观察到的向前的“V”字形模式,然而,将会影响人群整体的步行速度。
尽管过去的观测揭示了在行人的人群中群体的存在,但是对于移动群体的空间自组织以及对整体人群动态的影响确实未知的。结合用一个适当的扩展的交互模型所观察到的现象,我们已经证实了在群体成员之间的社会交往能产生一个典型的群体自组织。
我们的经验观察表明,大部分的行人行走行为(pedestrian traffic)实际上是由组的形式形成的。在我们的数据中,只有三分之一的行人单独行走。而且,也证实了行人群体行走的形式对于整体行走效率有着重要的影响。这突显了在更深远的行人动力学的研究方面,考虑群组是有必要的。
我们发现,典型的群体行走模式出现在群体成员之间的局部相互作用。在低密度时,组成员倾向于并排行走,形成一条垂直于行走方向的线,从而在街道上占据一个大区域。因此,当局部密度水平的增加,组需要适应去减少适当的空间。当组内有三个或四个成员时步行模式分别形成“V”字型和“U”字型。正如数值模拟所示,这些情况是由每个行人倾向去找到一个舒适的步行位置以支持与其他组成员沟通而形成的突发模式。
然而,步行效率事实上是有相当大的影响,“V”字型和“U”字型的群组方式是凸形状,但是这没有实现最佳的“空气动力学”效果。事实上,一个凹形如一个倒“V”形,将是有利的因为它支持移动到人流中(就像迁移鸟类的飞行编队如鹅或鸭以降低空气阻力[26,27])。
其他的计算机仿真表明该模型参数 代表成员之间的社会相互作用的强度是捕捉系统动态的本质(见图6a)。当 被设置为0(即当组成员只作为一个整体而没有通信交流时),逆V字型的形状产生了并且步行速度接近一个孤立个体的行走情况(比较图6中的虚线和暗灰色曲线图)。相比于 = 4时,从我们的实证结果所确定的值表明,速度平均减少了17%(见图中亮灰色曲线)。因此,两个相互矛盾的倾向是:如何走快速时有效地最小化摩擦(产生逆“V”字型的行走情况),以及在群成员之间有社会交流(支持“V”字型行走情况)。在非常低的密度,这两种倾向是兼容的,因为行人可以并排走并接近期望的速度。在中等密度,情况发生了变化,就如观察到的那样,在支持V和U字型行走形式的情况下社会交流的作用被给予了更大的重视。然而,当密度达到很高的水平时,就会出现物理上的限制会大于社会层面的因素,而小组成员将开始以队列的形式一个接着一个,形成一个“河流“形状的模式,就像Helbing等人报道的那样[ 28 ]。
或许有人要问当超过四个成员形成组时应如何组织。事实上,例如有十个人是不可能并排着走的。这就要求每个小组成员都想同时与所有的人进行交流。相反,遇到大的群体(如旅游团或远足团体)通常会分裂成小群体。对群体实现分裂最可信的解释就是当群体成员太过远离彼此而不能沟通时,他们只考虑走向周围能彼此交流的人。因此,两人到四人组成的群组是最常见的。在我们的模型中,通过行人i的指定的中心点 来实现,这个概念并不是作为所有其他群体的中心,仅仅是对于少数人来说。
此外,有一个可能是在行人群体中作为主要的影响。例如,就如我们所知的群体成员之间的发言每个人的分布是不一样的。这种情况并不服从泊松分布,而是其中一些成员大部分时间讲,其他人则在听[ 29,30 ]。因此,在人群中说话多的人站在群体中间,而听的人则会走在两侧。同理,大的群体很可能分裂成一个个小的群体,而小的群体则围绕说话多的那个群体。这在未来的实验去测试这一假设将是有趣的。
总的来说,社会互动对于人群的自组织来说是一个重要的方面,并且在未来的人群行为的研究中必须要被考虑进去。这项工作不需要道德规范。行人人群的步行记录在公共区域进行,然后数据进行匿名分析。
经验观察:
人群A的观察是在2006年的春天,位于法国的图卢兹进行的;而人群B的观察是2007年的春天的一个星期六,在一个步行街上进行观察的。在准备好相应的数码相机等设备之后,把A、B的频率分别设定为1帧/s和5帧/s,而 A/B的平均全局密度水平为:0.03和0.25peds/s。在这两个群体中,每个组的速度被计算为其组成员的平均速度。不考虑平均行走速度和空间形态的计算(包括密度测量)。
模型与仿真设计:
在图4的说明中给出的模型参数代表一个系统扫描的参数空间的校准结果,这组运动用合理范围的参数值进行模拟,以确定形成最佳观测效果的参数组合。相比于经验数据,表1是基于行人之间平均角度和距离值。
在我们的计算机模拟中,行人开始是处于随机的位置和平行于街道行走方向的随机行走行为。每组的成员之间刚开始相聚一米以外的距离,然后具有相同期望的行走方向。所需的速度通常分布的平均值为1.3米/秒和标准偏差为0.2米/秒,以反映行人行为的自然改
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[154070],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


