
英语原文共 29 页
第二章
轮胎建模的基础因素
2.1介绍
以力和力矩形成动力结构的轮胎的性能是多个方面共同作用的结果。涉及轮胎主要的工作因素可以与涉及(通常是重要的)次要影响因素之间区分开。
在表2.1中,这些因素以矩阵的形式呈现。(准)稳态和振动行为有更深的区别,在对称(或平面内)和反对称(或平面外)之间也是如此。主要工作因素以粗体字母出现。其余因素则为次要因素。
在三个垂直方向上的传递力主要需求()以及使车辆克服道路不平整的主要需求,涉及到横向和纵向扭曲和滑动之类的一些次要因素。虽然被当作次要现象,但其中涉及的一些量对于产生变形和相关的力是重要的,并且在整个系统中作为输入变量处理。
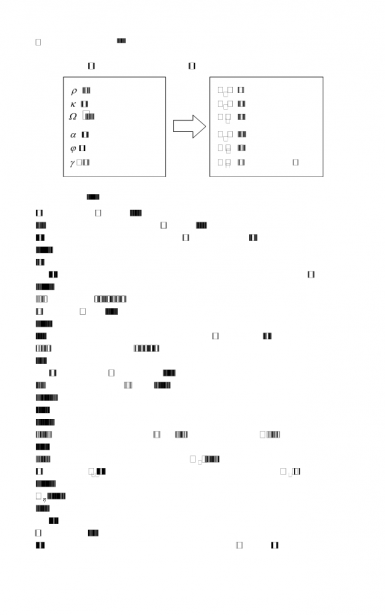
表2.1 轮胎因素
|
主要工作作用和次要影响 |
|||
|
(准)稳态 larr;→ 瞬态/振动状态 |
|||
|
对称(平面内) |
承载 制动/驱动 滚动阻力 |
径向偏转 切向滑动 和扭曲 |
缓冲 齿啮式联接 固有振动 |
|
反对称(平面外) |
转弯 轮胎拖距 倾覆力偶 |
侧向和旋转/转向的滑移 和扭曲 |
相位滞后 不稳定 固有振动 |
图2.1 输入/输出量(路面视为平坦)
图2.1显示了输入和输出组件的量。在这张图中,假设轮胎是均匀的,并在平坦的路面上移动。输入量来源于车轮相对于道路的运动。下一节给出了这些输入量的精确定义。
对于偏离直线运动的小偏差,可以给出直线运动的线性描述。这样就有利于认识到对称轮胎系统对称和反对称运动的响应是不耦合的。图2.2显示了具有输入和输出量的独立函数块。在这里,我们还考虑了从路面几何形状的变化和轮胎不均匀性输入的可能性,例如,不圆度、刚度变化和内置力。
力和力矩被认为是输出量。当认为是刚性的时候,假设有时这些力作用在具有惯性特性的刚性圆盘上是助动的,则等于轮胎的惯性性能。这些力可能不同于作用于道路和轮胎之间的力,因为当相对于车轮轮缘振动时,对轮胎的动力作用。车轮轮缘的运动和路面的轮廓,以其高度W及其在接触中心或附近的向前和横向斜率表示,被视为轮胎的输入量。认为制动和驱动力矩作用于转动轮惯性I。对于自由滚动轮胎(定义=0),主轴的轮对角运动仅受内动量M的控制,作用于轮缘和轮胎之间。然后,车轮旋转轴的五个运动分量可以作为输入量。
关于轮胎的力产生和动态特性的讨论将沿着两条主线进行:对称和反对称行为。这些主要输入运动组之间的相互作用使情况复杂化(组合滑移)。如果
图2.2 轮轴运动和路面坐标以及可能未耦合的轮胎系统块对与稳态直行运动的微小偏差有效
至少有一个输入运动,或者更准确地说,其中一个相关的滑动部件变得相对较大,这些相互作用就变得很重要。由于其相对简单,将首先处理稳态行为(第3章)。关于轮胎动态性能的讨论始于第5章。
2.2 轮胎输入量的定义
如果要考虑的问题涉及到道路的不规则,则必须根据道路上遇到的特定不规则了解短轴(主轴)的位置和方向。路面是根据附着在道路上的轴的坐标系来定义的。如果已知轴相对于固定三轴架的位置和方向,则可以确定车轮相对于可能不规则路面的确切位置。车轮相对于道路的相对位置和方向对于推导子午线轮胎偏转和相对姿态(外倾角)以及评估摩擦系数的当前值很重要,这些值可能会因滑点或非均匀表面条件(凹槽)而变化。这种相对位置的时间变化率不仅需要考虑可能的滞后效应,而且主要是为了确定车轮相对于地面的所谓“滑动”。
如果接触面附近的路面可近似为一个平面(即,当分解表面垂直剖面的最小考虑波长相对于接触长度和其振幅较大时),则除几个滑动量和车轮的运行速度之外,车轮中心与道路平面的距离以及车轮平面与路面法线之间的角度也是足够的。
对于图2.1中列出的各种运动和位置输入量的定义,有助于分析图2.3。其中绘制了许多平面。道路平面和车轮中心平面(具有沿单位向量l的交叉线)以及两个垂直于道路平面的平面,其中一个包含向量l,另一个包含沿车轮旋转轴定义的单位向量s。从图中可以看出,接触中心C的定义也被指定为(三个平面的)交叉点。单位矢量t位于路面上,垂直于l。矢量r形成车轮中心A与接触中心C之间的连接。其长度r定义为轮胎的加载半径。车轮相对于惯性三轴的位
图2.3 定义车轮的位置、姿态和运动,以及由道路作用在车轮上的力和力矩,所示方向定义为正方向
姿完全由向量b a和s描述。道路平面在接触中心由该点c的位置矢量和该点中道路的法向(单位矢量n为正向上)定义。图2.3还显示了两个轴系统(惯性三轴架除外)。首先,我们介绍了道路接触轴系统(C、x、y、z),其中x轴沿交叉线(l)向前,z轴沿垂直于道路平面(-n)向下,y轴沿横向单位向量t向右。其次,轴(A、xi;、eta;、zeta;)的轮轴系统用xi;轴平行于x轴,eta;轴平行于车轮主轴,zeta;轴沿着半径(r)。文献中的符号约定并不统一。
为了方便和减少出错的来源,我们选择了一种符号约定,尽可能避免使用负数量。
轮胎rho;的径向偏差定义为轮胎半径从空载状态下的减小到负载情况下的r:
(2.1)
若rho;为正的,车轮负载F(正向上)也是正的。
切向或纵向滑动k需要更深入的分析。为了正确定义纵向滑动,引进了一个滑动点S。这一点被认为附着在轮辋或轮身上,其半径等于滑动半径。当车轮以等于零的纵向滑动滚动时,形成旋转中心。滑动半径是滑动圆的半径。在消失的纵向滑动中,这个滑动圆纯粹在平行于路面的假想表面上滚动。滑动半径的长度取决于所采用的纵向滑动的定义。直线前进的定义是使滑动半径等于加载车轮半径。然而,这将已经导致相当大的纵向力,在等于零的纵向滑动时产生。一个更方便和物理上更正确的定义对应于在零纵向滑动时f=0的情况。由于滚动阻力的出现,因此测量轮胎特性需要施加驱动扭矩,以达到滑动等于零的条件!
这一点可能变得非常重要,尤其是在大外倾角下进行试验时,阻力可能会变得相当大(摩托车轮胎)。另一种常用的定义是以自由轧制时定义的有效轧制半径(=0)作为滑动半径。在正常情况下,根据后两个定义得到的与k图非常接近。曲线的水平微移动足够精确,可以从一个定义更改为另一个定义。最后一个定义的缺点是,当在非常低的摩擦(结冰)表面上进行测试时,滚动阻力可能太大,无法让车轮在不施加驱动扭矩的情况下旋转。因此,在这种情况下,不能实现自由轧制状态。然而,我们将采用最后一个定义,其中=,因此,点S位于距离车轮中心处。图2.4描述了这种情况。
图2.4 有效滚动半径和纵向滑动速度
根据这个定义,当车轮在平坦平坦的路面上以恒定速度自由滚动(即:在=0时),纵向滑动k等于零。尽管如此,在自由滚动时,由于轮胎中存在产生滚动阻力力矩的迟滞,会发生一些前后变形。由此产生了滚动阻力=/r,这必然伴随着切向变形。我们可以同意,在观察的瞬间,位于滑动圆上并附在轮缘上的点S已达到其最低位置,即:在沿半径向量r的直线上。在自由滚动时,其速度已等于零,点S已成为轮缘运动的旋转中心。我们在平坦的道路上自由翻滚处于直立位置(gamma;=0)或没有车轮横摆率( =0)的车轮,参考图2.3,车轮中心向前(x或xi;)方向的速度:
= (2.2)
后面用Omega;表示待定义的轮身转速。利用这一关系,可以通过试验来评价有效轧制半径的大小。当轮轴在平坦路面上沿直线移动时,测量前进速度和车轮转速。两个数量的划分导致的出现。有效滚动半径将是正常载荷和行驶速度的函数。我们可能需要考虑到对外倾角和滑动角的依赖性。
如果在制动或行驶时,纵向滑动不再为零,则点S将以不为零的纵向滑动速度移动。很明显,如果 =0:
(2.3)
(2.4)
纵向滑移(有时称为滑移率)用表示,可以暂定为S点的纵向滑移速度-与车轮中心的前进速度之比:
(2.5)
这同样适用于平坦道路上的车轮,且 =0。稍后将给出有关k的精确定义。选择纵向滑动为标志,因为在行驶时,当gt;0时,为正,在制动时,当lt;0时,为负。当车轮锁定(=0)时,显然有 =-l。在文献中,符号s(或S)更常用于表示滑动比。
滚动的角速度,更精确地定义为在起伏路面上移动的情况下,是连接S和A(该半径被认为与车轮相连)的半径与图2.3中定义的半径r(始终位于通过车轮旋转轴与道路垂直的平面上)之间角度的时间变化率。图2.5说明了这种情况。
滚动的线速度,定义为假想点C位于沿半径向量r的直线上,在观察瞬间与点S重合,相对于固定在轮缘上的点S向前(x方向)移动:
(2.6)
对于自由滚动的轮胎我们可以得到=, =0和=。注意,在车轮锁(=0)处,当车轮在垂直弯曲轮廓的道路上移动时,滚动的角速度r不等于零(因此,车轮的同一点并不总是与道路接触)。对于出现横摆率的弧形车轮,即使车轮中心速度=0,在平坦路面上也可能发生快速滚动。在这种情况下,滚动的线速度上升,=sin,因此滚动的角速度=sin。
图2.5 轮胎在起伏不平的路面上滚动和打滑
在近似水平路面的正常情况下,旋转速度Omega;可定义为通过车轮主轴轴的垂直平面上的轮身(轮缘)角速度。在平坦的道路上,滚动的角速度和车轮的旋转速度Omega;是相等的。车轮绕主轴旋转的绝对速度与-不同,当车轮呈弧形时,通过主轴轴的平面会出现横摆率,并且与道路垂直。详情参见图2.6。
(2.7)
该方程为非水平路面上的一般定义提供了正确的基础。如果可以从车轮动力学计算中获得,则其计算是直接的。
纵向运行速度定义为虚点沿x轴方向(向量l)传播速度的纵向分量(在半径向量r上)。如果车轮的移动方式使同一点与道路保持接触,我们将得到=。这与道路平坦且车辆变桨率为零时的车轮锁定相对应。对于自由滚动轮胎,纵向行驶速度等于线性速度,我们得出=。现在,纵滑的一般定义为:
(2.8)
横向滑动定义为接触中心C的横向速度与纵向运行速度之比。就滑动角而言:
(2.9)
对于不显示外倾角或径向偏转率和非零外倾角下横摆率的车轮,在平坦道路上行驶时,车轮中心的横向和向前速度之比为:
(2.10)
在实践中,点C和紧密相连,学术界常常
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


