英语原文共 30 页
轮胎和车辆动力学
Hans B. Paceika
代尔夫特大学名誉教授
TNO汽车代尔夫特技术咨询顾问
荷兰
第一章
轮胎特性与车辆操纵稳定性
1.1导言
本章的目的是介绍车辆动力学,重点是讨论影响轮胎性能的因素。分析简单汽车模型的稳态侧偏特性,瞬态运动大转向输入扰动对轮胎特性的影响,以及轮胎的各种形状因素对汽车操纵性能的影响。侧力与滑移角的斜率alpha;(侧偏或侧滑刚度)是汽车基本线性操纵性和稳定性的决定参数。轮胎特性与其起始偏移可能是导致所谓轮胎拉力现象发生的原因。侧(或侧偏)力特性进一步决定了车辆在较高的横向加速度下的操纵性和稳定性。转弯刚度与轮胎正常载荷的非线性关系对汽车的操纵特性有很大的影响。
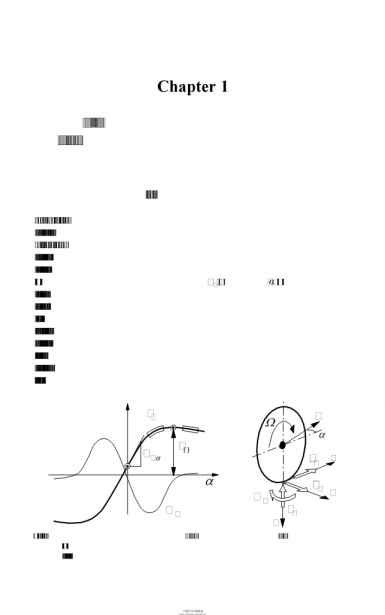
图1、轮胎或轮轴中可能影响到汽车稳定滑移力和力矩正方向的形状特征因素 (如图中所示的阴影部分)可参考附录1
在稳态操纵分析中,采用简单的单轨(两轮)车辆模型,引入前后轴的有效侧力特性来表示悬架和转向系统的设计因素,如转向柔度、转向横摇和横向载荷传递等,并在有效特性中考虑了可能施加的(适度)制动力和驱动力的影响。较大的制动力可能导致车轮锁定,并可能导致与未扰动路径相比的较大偏差。我们将在第三章(电刷模型)中应用简单物理轮胎模型的理论,对车轮锁紧引起的运动进行研究。本章还将简要介绍装卸稳定性理论在重型卡车动力学中的应用。特别要注意的是,当车辆振动运动的波长出现时,由于道路不均匀、制动力矩波动而引起的振动不稳定现象,即与拖车组合时出现的振荡不稳定现象。当车轮的振动波长不平衡或不稳定(晃动)或小于5米时,需要对轮胎响应进行非稳态或瞬态描述,以正确分析这一现象,在第5-8章中将讨论这些问题。这些应用证明了瞬态和振荡轮胎模型使用的必要性,并提供了有关车辆动力学的远见。第十章是对摩托车侧偏特性和稳定性的分析。
1.2轮轴特性
轮胎和车轴特性对道路车辆的动力学性能起着至关重要的作用。本节介绍了气动轮胎产生力和力矩的基本特性。讨论了轮胎的纯滑移特性和复合滑移特性,并给出了典型特征。最后,根据悬架和转向系统的独立轮胎特性和相关性能,推导出所谓的有效轴特性。
1.2.1轮胎特性介绍
直轮自由滚动,即不施加驱动力矩且无侧滑,并且是沿直线路面的运动,这种情况我们定义为无滑移的起动情况。克服轮胎滚动阻力所需的拉力相对较小,由于轮胎结构不完全对称,可能会产生侧向力和(自)对齐力矩。当车轮运动偏离此定义零滑移条件时,车轮滑移会伴随着轮胎变形的累积,在接触补片产生部分滑动。结果将导致(额外的)水平力和对准扭矩的产生。这方面的机制在后面的章节中的尾部将被提到。现在,我们将定义各种滑移量作为输入轮胎系统的力矩和力。输出量(正方向,如图所示,图1.1)还有几种不同的定义也在使用中。附录一给出了自由滚动轮的滑移、弯曲、输出力和力矩的各种标志,并给出了相应的特征:正向速度V(车轮中心速度矢量的纵向分量)和转速的角速度Omega;。通过对这两个量的除法,得到了所谓的有效滚动半径r
虽然对制动轮也可以定义有效半径,但我们将其定义限制在自由滚动的情况下,当施加扭矩时,在车轮自旋轴上将产生纵向滑移。其定义如下:
对于正的为正纵向力或提升力,即:一种动力。在这种情况下,车轮角速度Omega;随着Omega;相对增大,因此Omega;大于Omega;。在制动过程中,前部和后部的滑移变成负值。在车轮锁上,很明显,=-1。在光滑的道路上行驶时,可以达到很大的数值。为了将滑移限制在最大值1,在某些文本中,在滑移的驱动范围内,纵向滑移被不同的定义:在(1.2)中的分母Omega;被Omega;代替。这是之前的文本中所没有做的。
侧轮滑移被定义为横向车轮滑移和车轮向前速度部分的滑移。这对应于减去切线的滑动角alpha;(图1.1)。再一次,当边缘力在正滑移角处时符号alpha;被选择。
图1.2边缘力和刹车力的结合分析
第三个也是最后一个滑移量是所谓的旋转,这是由于车轮围绕一个轴正常的道路旋转。当alpha;保持为零时,轮曲面或者说是倾斜角gamma;导致路径曲率,而倾斜角或者是车轮平面围绕x轴的弯曲,共同影响着自旋。当从车轮后面向右倾斜时,弯曲角被定义为正数。在第二章中,我们将给出更精确的车轮滑移三分量的定义。力F,F和力矩M取决于输入角度,它们是滑移部件和车轮载荷的函数。对于一般的稳态直线运动,我们有以下公式:
垂直载荷F可视为由轮胎正常挠度引起的给定量。通过对给定速度、道路和环境条件的测量,可以得到该函数。图1.1显示了所采用的轴系(x,y,z),速度、力和力矩为正方向。唯一的例外是F来自从路到轮胎的垂直力。实际上,该力被定义为向上方向的正力,因此等于轮胎的正常载荷,并且Omega;相对于负y轴(不提供y下标)也被定义为正。注意,轴系符合SAE标准(SAE J670e,1976)。另外,滑动角的符号是相对于图中的SAE定义(参考见附录I)选择的。
图1.2描述了典型的纯(=0)和纵向(alpha;=0)时的滑移特征,并给出了一些组合滑移曲线,其中拱形角gamma;保持为零。我们将纯滑移定义为纵向滑移或横向滑移不同时发生的情况。数据表明,当添加另一个滑动部件时,会出现力的下降,由此产生的情况被定义为组合滑动。力的减小可以简单地解释为总水平摩擦力不能超过由当前摩擦系数和正常载荷决定的最大值。在后面的第三章中,当考虑一个简单的物理轮胎模型的行为时,这一点变得很清楚。表格中还包括了制动滑移率最终达到与车轮锁相对应的100%(k=-1)值时的相对应的情况。
图1.3规范侧偏刚度、峰值侧力和侧力随正态竖向荷载和滑移角变化的典型特征。
纯滑移曲线的斜率分别定义为纵向滑移刚度和横向滑移刚度。轮胎的纵向滑移刚度表示为C,轮胎的横向滑移刚度或侧偏刚度表示为它们是轮胎最重要的性能参数,对车辆的操纵性能和稳定性性能起着至关重要的作用。减对齐力矩与滑移角曲线的斜率(图1.1)称为对准刚度,用C表示。负对准力矩与侧力之比为空气轨迹(如果忽略了第四章所要处理的所谓剩余力矩)。这个长度是在接触中心后面的距离(按车轮平面方向将车轮中心喷射到地面上),直到发生侧向力作用的点。线性化的力和力矩特征(在小滑移水平上有效)可以用下列表达式表示,其中包含了曲面的影响。
这些方程的排列方式使所有影响(力、力矩、滑移和弯曲刚度)变为正量(不包括一些例外情况)。
值得注意的是,当侧偏刚度表示为弧度时,轮胎侧偏刚度的数量级约为垂直车轮载荷的6至30倍。旧的斜交轮胎结构的价值较低,现代赛车轮胎的价值则很高。纵向滑移刚度通常比侧偏刚度高50%左右。气动尾迹的长度相当于侧力接触贴片长度的四分之一。
图1.3中给出了一些有趣的图表,是影响汽车操纵性能的重要因素。这些特点是典型的卡车和汽车轮胎所具备的,并且基于了在密歇根大学运输研究所(UMTRI,前身为HSRI)进行的实验,参考文献(Segel等人)(1981年)。汽车轮胎的侧偏刚度是根据最新的研究结果得出的。结果表明,侧偏刚度随车轮载荷的变化不成比例。汽车和卡车轮胎的水平和坡度也有明显的差异,当与额定或名义负荷的关系正常化时,也会出现明显的差异。在不同的车速和路面条件下,角环力与滑移角的关系表明,零滑移角下的坡度不受速度水平和湿、干条件的影响,也几乎不受速度的影响。当路面干燥时,峰值力水平变化不大。在潮湿路面上,出现一个更为明显的峰值,峰值水平随着速度曲线的增加而显著下降,曲线的形状类似图1.3的侧力特性,可以用一个已知的数学公式来表示,这个公式已被命名为魔术公式,第四章给出了与此公式相关的经验轮胎模型的完整处理。目前,我们可以给出侧力和侧偏刚度的表达式,
包括刚度因子
B=C/(CD)
峰值因子 (1.6)
D=F(=F)
侧偏刚度
C=(BCD)=csin{2arctan(F/c)}
形状因子C和E,以及参数c、c和摩擦系数mu;(可能取决于垂直载荷和速度)可以通过计算方法来估计和确定。
1.2.2有效轴侧偏特性
基于对稳态车量特性的分析,一种简单的两轮车辆模型可以成功地应用。悬架和转向系统的屈从性和柔顺性,如转向柔顺性、车身转速和轴向载荷传递等,可以通过使用有效的轴特性来考虑。当我们意识到对于瞬态或振荡的托利运动时,对稳定状态的限制变得明显,显示出偏航和滚转加速度,以及在各阶段中的差异,并且像滚动角和载荷转移这样的浮动因素不能再被写成一个横向轴力(前或后)的直接代数函数。因此,如果输入信号的频率(如方向盘角)相对于车身滚转固有频率不能被认为是很小的,那么就应该放弃考虑有限重心高度影响的简单方法。由于方向盘张紧和转向系统的固有频率相对较高,因此在有效特性中包含转向机构的情况下,对稳态运动的限制就不那么重要了。Chiesa和Rinonapoli(1967)是最早采用有效轴特性或“工作曲线”的人。Vagstedt(1995)同样通过实验定义了这些曲线。
在评估完整的非线性有效轴特性之前,首先我们将在简单的线性两轮模型中使用有效侧偏刚度的推导。为确定车辆模型,必须对更全面的车辆模型进行定义。
图1.4描绘的是一个三自由度的车辆模型。向前的速度我可以保持不变。作为运动变量,我们定义了参考点A的横向速度v、偏航速度r和滚动角Psi;。引入了一个运动轴系统(A,x,y,z)。x轴指向前方,同时位于地面平面和与经过所谓滚动轴的群垂直的平面上。y轴指向右侧,z轴指向向下。当滚转角等于零时,后一轴穿过重心。用这种方法定义了参考点A的位置。到前轴的纵向距离是a,到后轴的距离是b,两段距离之和是车轮底座l,我们可以在曲线中写明:a-a和b-a。
图1.4车辆运动有三个自由度:横向,偏航,以及旋转
在曲线中,车体绕着旋转轴旋转。这个虚拟轴的姿态是由前后滚中心的高度h来定义的。滚动轴的定义是考虑车身的运动相对于地面上车轮的四个接触中心,在作用于重心的外部侧向力的作用下进行的。由于车辆配置的对称性和模型的直线性,这些位置可以认为是固定的。滚子中心位置由悬架运动学和可能的悬架横向柔顺控制。图中描述的扭转弹簧表示了前、后横摇刚度C的大小,它是由悬架弹簧和防滚子杆组成的。物体重心前后的位置是由a和b决定的,它的高度是从h到滚轴之间的距离。物体质量由m表示,质心、水平轴和垂直轴的转动惯量分别为I、I和I.当建立运动微分方程时,后一阶段将需要这些量。没有弹簧的质点将被忽略,或者它们可以作为点质量被包括在滚轴上,从而使它们成为弹簧质量的一部分,也就是车体。
此外,该模型是扭转弹簧周围的转向轴,国王销(king-pin)是定位在一个小的连铸机角上的,铸机长度为e,如图所示。转向扭转总刚度,为左边和右边之和,以C表示。
有效轴侧刚度线性分析。
在相对较小水平的横向加速度时,允许使用近似的轮胎特性,其所代表的只是斜率在零时的滑移。我们将首先推导出在这些条件下可以使用的有效轴侧刚度。载荷传递、车身滚转、转向柔度、侧力转向和初始弯趾角的影响将包含在有效轴侧刚度的极限表达式中。
并给出了轮胎侧向力和对中力矩的线性表达式(1.5)。这些表达式中的系数是垂直荷载的函数。对于与平均值有关的微小变化(以下标o表示),我们为转弯和弯曲力刚度编写了线性化表达式:
其中,车轮垂直荷载的增量用表示,F=F处的系数与载荷曲线的斜率用zeta;表示。
当车辆在圆周路径上平稳地行驶时,这时出现向心加速度a和离心力K=ma可以说是作用在重心相反方向的车身上。假设滚转角Psi;较小,计算方法是将滚转轴的弯矩除以表面滚刚度,该刚度随项的增加而减小。
滚转轴的总弯矩分布在前后轴上,与前滚刚度和后滚刚度成正比。在具有向心加速度的稳态侧偏运动中,从轴i(=i或2)处发生的从内到外轮的载荷转移由轴的载荷传递系数决定,另考虑到带有向心加速度a的稳态转弯运动,我们得到:
i轴的荷载传递系数
滚动轴相对于水平的姿态角被认为是小的。在公式中,s为轨道宽度的一半,h是从质心到滚动轴距离的距离,a=a,a=b。在考虑了左、右两种载荷增量后,轴i处的左(L)和右(R)轮的垂直载荷就会增加。
前轴的车轮销delta;通过转向比n与施加的方向盘角delta;直接相关。
除此之外,通过悬挂运动学,车轮还可以显示出由车身滚动引起的转向角和弧度角。与滚角的函数关系可以线性化。我们给车轴下了定义
转向顺应性会产生额外的转向角,这是由于外力作用于大头针(转向轴)。对于一对前轮来说,这种扭矩是由侧向力(当然也来自于这里不考虑的驱动力或制动力)产生的,它通过力矩臂对大头针施加了瞬
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。