
英语原文共 30 页
文献翻译:Tyre And Vehicle Dynamics(车辆与轮胎动力学P150~180)
由于方程3.124可以化简为查表求解的Bessel微分方程,其精确解可以求得。在给出完整解答过程实例之前,我将先进行轻微干扰作用之后的运动分析,这将允许我们把方程中的变量进行近似替代转换为常数:用初值u0代替u。这样一来等价方程的求解就容易得多。于是我们可以得到方程3.127。
3.121
3-122
3-123
这里D1,2作为集合常量(取决于状态变量v和r的初始值),而lambda;1,2代表固有值,即等价方程的特征根。
通过比较方程3.124的系数,可以找到A,B,C,D的表达方式。因为很显然前三个数是正值,而且在这个例子中C2远小于C1,这使得D也是正值,我们期望这个等价系统的不稳定条件唯一,即第三系数可能取得负值。于是,其中一个根(也就是lambda;1)成为正值(它是实数的话)。显然这只出现在u是正值的情况下:当后桥的轮子被锁死时。当系统的u值小于零时,前轮将被锁死,这不会使得系统的稳定性降低,但会使得汽车无法操控。这是由于锁死的轮子剪切角再怎么改变也无法影响摩擦力矢量的方向。后桥锁死的汽车模型可以对应汽车过度转向前轮锁死的情况,这将引发更严重的操控失灵。通过将方程3.128或3.124的第三系数取0可以得出这种后桥锁死状态的临界速度。
从这一表达式中可以看到,当前轮的刚性足够时(C1趋近于无穷大),我们可以得到简化的方程ucrit=root(mu;gl)。由于前转向的刚度一般是普通车胎载荷的6~30倍,前轮弹性造成的影响可以忽略不计。根据干燥路面取mu;=1我们发现临界速度大致在20km/h左右。
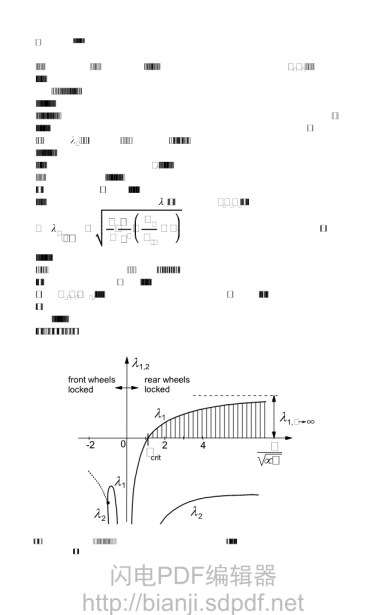
鉴于上述后桥锁死汽车失稳的临界速度之低(正常行驶时制动刹车时的速度将远大于这一速度),将不稳定的程度考虑为速度的函数将更有实际意义。这里采用一根lambda;1代表不稳定的等级。图3.42描述了lambda;1随着行驶速度变化的趋势。这一图表包括了前轮锁死的情况,此时很显然这一根取负值,并在高行驶速度下变得复杂(实部用虚线曲线表示)。为表达不稳定程度的实际情况,我们采用u趋近于无穷时的水平渐近线。
3-124~4.14
从方程中可以看出不稳定性在前轮的转向刚度更低时相应地减小,同时在后桥侧偏刚度很低时更加平衡。同样很显然的是,当前轮锁死时,不稳定程度也减小到0,和稳定性并没有关联。
通过使用Bessel微分方程的Lommel变形并在期结果中使用改良的Bessel函数可以得到方程3.124的解。这些函数方程可以通过查表的方式得到,具体参考文献是Abramowitz和Stegun的著作(变形方程是9.1.53,其解在p.377)。
在Koiter和Pacejka1969年的论文中,阐述了这一完整非线性系统的准确结果和数值计算结果的实例。在这一特殊情形下各个参数满足:a=b=k,B1=0,C1/mu;F2=6,此时线性方程的解可以通过图3.43表示。可以比较准确解和代换方程得到的近似解的差别。通过(u,v,r)三维空间的投影可以得到(u,r)平面轨迹,也就是画出了稳态和非稳态条件下的解。沿着u轴方向我们可以引入时间轴来考虑3.126中的关系。在这一考虑无量纲特征值lambda;1,2/(l/mu;g)实例中,给它分别赋值1.26-3.43。为了方便进行比较,两者初值被设定为相同的量。在两者的稳定衰减分支中观察不到可分辨的区别。然而,准确解的不稳定分支的时间取得更大的数值,这一区别以近似指数规律不断增大。在后桥趋向于分离的运动刚开始时,相符合程度非常好。可以看到随着时间的不断累积,其结果越发接近,并包括第三项(t2)。这一结果证实了我们定义不稳定程度这一选择的可行性。
沿着纵轴方向描述了横摆角速度。在到达峰值之后,摆角逐渐减小直到完全停止。曲线下方的面积和最终的摆角成比例。这个限定的摆角和变量r和v的初值线性相关。因此,关于最初直线运动路径的最终偏移量可以保持在任意选定的界限中,严格来说,这个实际系统总是稳定的。
最后,这个非线性系统的解决定于方程3.118、3.119,而轮胎特性由数值方法建立的运动方程如图3.41所示建立。现在,这一运动的特征将随着初始干扰级别的变化而变化。在图3.44和3.45中,展示了所描述的两种情况下的运动结果。其一,在前轮没有刹车的情况;其二,前轮在弱的刹车强度下(至少在最初发生滚动)的情况。最初行驶速度和干扰在两种情况下保持一定,但摩擦系数mu;发生改变。在低摩擦条件下,形成摆角所需的时间更多,并且我们发现这一角度可能超过180度。接下来锁死的轮子移动到前方(u<0),可以发现这种情况下在是稳定的震荡运动。在图3.44所示的情况中,mu;=0.25,我们确实观测到一次角速度符号的改变。当制动器同时作用在前轴是,减速作用更加明显,这时的我们完全停止所需的时间更短。总的来说,图3.45所示的最终摆角比3.44中的更小。阴影部分展示了前轮也被锁死时的变化范围。这显然会在滚动轮最初偏离角变得足够大并且超过图3.41所示特定值时发生,即到达倾斜直线的时刻。同时还发现,提高初速度的影响在定性分析上和减小摩擦系数是一样的。
第四章 半经验轮胎模型
4.1简介
在上一章中,我们基于轮胎的物理模型,介绍了轮胎受力和力矩的形成特性理论。这一模型的特殊之处在于把轮胎看成在整车模拟环境下属于汽车的一个零件。这种建模方式被称为“半经验法”,因为这个模型根本来说时基于测量数据的,但是也可以包含一些能够找到原始物理模型的结构,比如上一章节讨论的那些内容。数学模型的描述仅限于稳态情况。非稳态的系统表现将在接下来的章节介绍。
我们已经使用了几种数学方程来描述转向力的特征。我们尝试了指数、正切、抛物线(达到其极大值)和双曲正切(两种不同的)这几种不同的数学模型,分别达到了或多或少的成功。大部分情况下,只能实现特定的曲线拟合。为了提高精度,使用了测量数据表结合差值法。同时常用的还有高阶多项式,但是它被证明不总是能满足精度要求,而且在拟合原始数据曲线是出现很大的偏差。之后得到纵向力和校准扭曲的数学表达法并且它在经验描述中只和结合滑动状态相关。纵向摩擦系数作为输入参数代替了制动力或牵引力(在以往的汽车动力分析中常常使用这两个参数)。然而,在这个后来的理论中,牵引力和制动力仍然有着某些应用。
在本章接下来的部分中,首先会讨论一个基于相似性概念的简单相关方法;之后,本章剩下的篇幅会细致的描述一个轮胎模型的魔术公式。两种建模方法分别属于图2.11所示的分类二和分类一。
P157
4.2.相似性理论
这个小节要讨论的理论基于这一发现:当车胎行驶的条件和参考条件不同时,表现出的特性和纯滑动曲线在形状上几乎一样。参考条件的定义如下:当车胎以额定(名义)载荷(F20)运转,并处于外倾角等于零,无侧向滑动,给定路面条件的自由滚动条。曲线相似意味着属于参考条件的特征可以通过垂直和水平乘加和曲线的移动来再现。这一相似性理论最初由Pacejka在1958年使用,后来他又和Radt在1963再次运用。1983年Radt和Milliken在实践上的例证应证了相似性原理确实在近似条件下存在,并在1995年由Milliken和Milliken得到了相似的发现。图4.1和4.2展示了当力、力矩和偏角都被标准化的结果,得到了沿轴方向无量纲的值。原始数据经过处理后得到的初始图像可以变现相关特征。曲线来自于魔术公式的拟合。关于无量纲侧向力和无量纲力矩的参数B`、C`、D`和E`被用于无量纲版本的魔术公式(公式1.6)。之后这个公式将在4.6.10再次介绍。
结果得到的模型以它的简化程度和相应的快计算速度著称。考虑了外倾角的影响之后,这一公式能很好地表示纯滑动条件。结合侧向和纵向滑动条件的解释上能给出令人满意的定性分析结果。然后由于是定性分析,在两者结合的滑动量更高时,可能会出现偏差。
4.2.1. 纯滑动条件
这个函数代表了关于指定下标o注明的纯滑动条件下的参考曲线。例如参考方程Fy=Fyo(alpha;),代表侧向力关于偏离角在载荷为名义载荷FZO,纵向滑动和外倾角等于零且摩擦等级为mu;o条件下的关系。我们现在可以试着把条件改变为不同的轮载荷Fz。两种基本的变化将随着特性出现:(1)阶段变化将在侧向力饱和的处曲线(峰值阶段)发生。(2)斜率将在侧向滑动消失时(alpha;=0)变化。第一种调整是通过同时改变水平方向和垂直方向的特性(即Fz/Fzo的比值)实现的。水平方向的乘算需要不妨碍初始斜率。最终我们得到一个新的方程(方程4.1),和等效偏离角(方程4.2)。
由于Fyo关于幅角alpha;eq为0时的衍生显然等于初始转向刚度CFalpha;o,我们发现Fy关于alpha;的偏离在值上等于alpha;=0时的斜率(方程4.3)。这证明了初始条件下的斜率会受到逐次相乘的影响。对原始曲线的第二步操作是斜率的调试。这项工作通过一种包含新特征的水平乘法实现,即把幅角和新旧转向刚度之比相乘。最终得到 一个新的幅角值alpha;eq:(公式4.4)。
结合公式4.1,我们得到一个新的公式来表示侧向力和偏离角在新载荷条件Fz作用下的关系。在图4.3中,描述了 这两个得到新 4.15~4.29
曲线的相关步骤。这里的名义载荷Fzo=3000N,新载荷Fz=1500N。
在同一张图上,回正力矩的特性也适应了新的条件。考虑到这一点,我们利用了从刷形模型(图3.4)上得到的经验。更明确地说,我们将遵守这一理论相关的法则,很显然,Mz曲线达到alpha;轴的点在Fy曲线峰值的下方。在图3.4中,这一情况取得的条件是tanalpha;=1/theta;y。这一结果意味着等价偏离角必须用作Fy方程的幅角。第二,我们将使用关于新回正刚度值的信息。使用的Mzo参考曲线相比图3.4的理论曲线更接近实际情况。典型特征之一就是惯量的符号在更高的偏离角范围处(Fy峰值)改变了。
由同样的的等价偏离角和归正刚度结合相似性概念,我们得到了规整力矩的新表达式:方程4.5。为了保持原斜率,第一个第三个因数是4.4中使用的乘数的相反数。第二个因数是中间量垂直方向曲线Mz的系数(图4.3中的1),它用于将斜率在不干扰alpha;范围的条件下和新的值相适应。需要注意的是,结合的第二第三因数等于新旧轮胎拖距之比值。
为了结合图像4.3进行相关计算,我们用魔术公式描述相关参数。于是归正刚度被看做接触长度2a和转向刚度某个部分的乘积。这四个参数值的最终结果在4.3和4.4两图中是符合实际的。用的相关公式如下:
P161
名义载荷下的侧向力:公式4.6
刚度系数:公式4.7
侧向力峰值通常和纵向力不同,我们在mu;yo之外引入mu;xo;公式4.8
转向刚度关于车轮载荷Fz的表达式:公式4.9。
归正力矩在名义轮载荷下的表达式:公式4.10。
刚度因数:公式4.11。
峰值(a0表示名义载荷下接触长度的一半):公式4.12。
归正刚度关于轮载荷的方程:公式4.13。
显然轮胎拖距t=c4a。接触长度a的一半被认为是和轮载荷的平方根成比例关系:公式4.14。
结果得到的轮胎拖距近似值足以被用于魔术公式轮胎模型方程来进行进一步研究。各个用于计算的参数值被列在了表格4.1。
P162
接下来的两个部分我们要解决摩擦系数的转换和外倾角gamma;的介绍。第一次转换由径向曲线和比因数的相乘实现。结合载荷的变化我的发现:公式4.15和公式4.16。
我们假定摩擦系数和滑动速度Vs有关。为了建立湿路面条件下的模型,我们使用了衰减函数mu;(Vs),参考方程4.E23。
考虑到图3.35c在计算的小外倾角条件下特性,我们需要水平调整Fy的曲线来得到可靠地结果。随后,我们保留侧向力的峰值不变,这一假设不总成立,因为实验中证实偶尔会出现轻微的侧向力峰值增加,或者是用恒定摩擦和有限接触宽度条件建立的物理模型计算时会出现轻微的减少。角度较小时,外倾推力接近于外倾刚度和外倾角的乘积。最后得到alpha;的偏移量:公式4.17。所以有公式4.18,这使得公式4.16中的alpha;eq随着alpha;被替换而增加。不太大时,
在新的条件下表达校准惯量变得更加复杂。我们从图3.35c发现偏离角不太大的时候,原始曲线Mzo随着力的作用同时有斜向和向上偏移的趋势,力矩将在力曲线穿越alpha;轴的时候变成零。当alpha;=0时,会得到一个值等于CMalpha;SHy的力矩然而,这个力矩应该是等于CMgamma;gamma;,同时外倾角力矩刚度CMgamma;为正值。这意味着额外的垂直偏移可由以下表达式得出:公式4.19。
P163
这一附加的力矩符合所谓的残余转矩Mzr,即侧向力为零时的残留力矩。如图3.35c所示,在偏移角取得更大值时,附加力矩应该趋近于零。通过将4.19式按a方
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


