
英语原文共 30 页,剩余内容已隐藏,支付完成后下载完整资料
- 195/65 R15汽车轮胎的回正力矩特性。魔术公式模型计算结果与使用Delft轮胎测试拖车(2000年)进行的测量数据(虚线)进行比较。
- 乘用车轮胎在福特的MTS平板trac III轮胎试验机(V.D. Jagt, 2000年)进行测试的翻车力偶和载重半径。与图4.29进行对比。
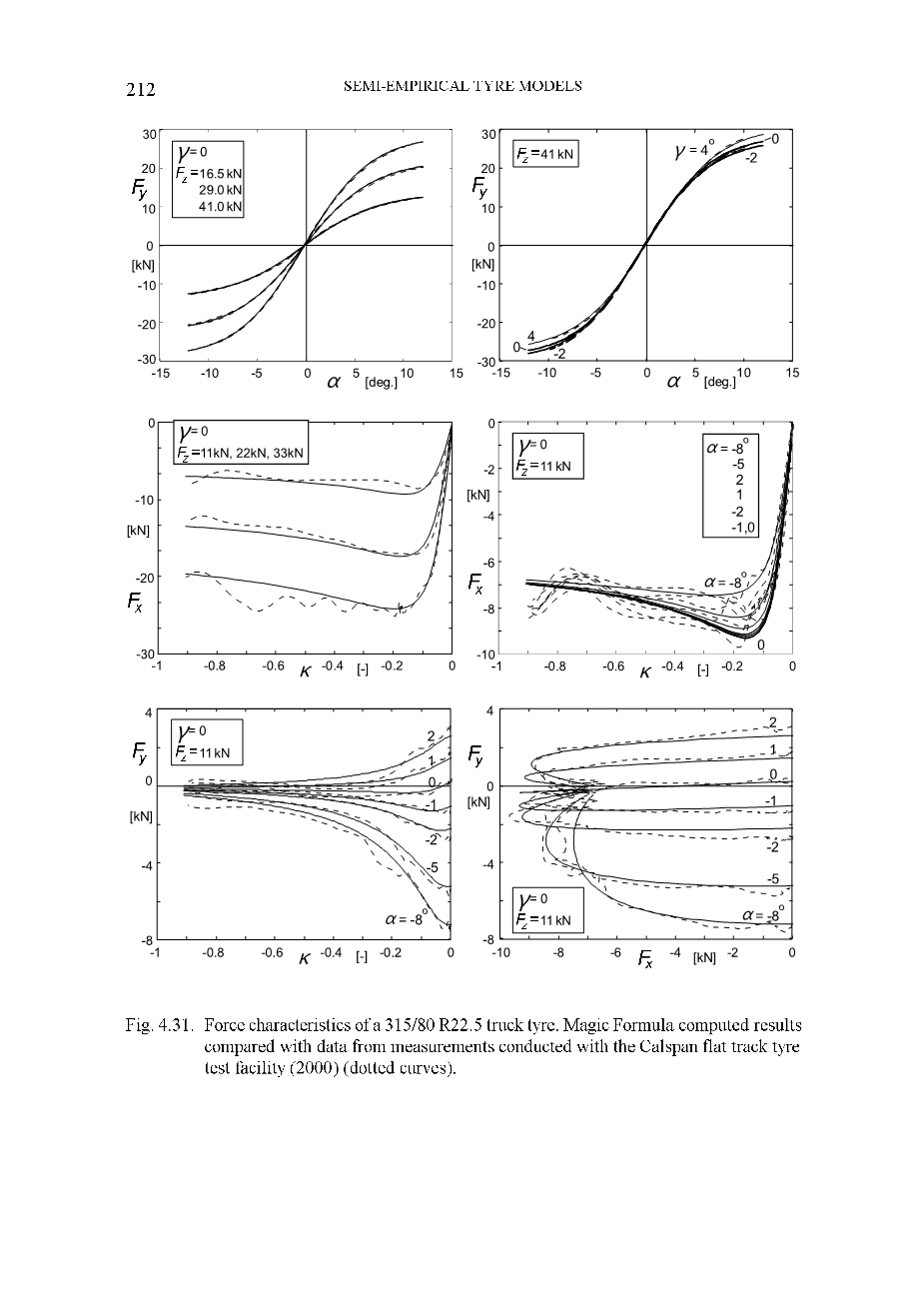
- 315/80 R22.5卡车轮胎的受力特性。魔术公式计算结果与Calspan平轨轮胎测试设备(2000年)的测量数据进行了比较(虚线)。
- 315/80 R22.5卡车轮胎的回正力矩特性。魔术公式计算结果与Calspan平轨轮胎测试设备(2000年)的测量数据进行了比较(虚线)。
练习4.1 以作为输入量的轮胎侧力特性和组合滑移特性的评估
以图4.33中的图表为例。对于原(公称)侧力特性和转弯刚度相对轮载特性,采用所给公式(4.6-4.9),使用如图所示数据。假定凸度刚度随车轮载荷的变化为线性。为涵盖合并滑移情况,请使用公式(4.41-44)(注:
以N/度表示,先将其转换为N/rad以符合公式(4.42))。在公式(4.42a)中选用。在正常情况下我们有如下参数:
。
使用公式(4.45,46)并进行以下操作:
图4.33 以纵向力为输入量,采用相似法评估滑轮胎侧力偏离公称和组合特性(练习4.1)。
- 推导并绘制函数用于描述轮胎在不同条件下的参数值:
- 对于固定的滑移角 和8°,在 和的条件下,绘制 的图形。
练习4.2 以为输入,采用魔术公式和相似度法对纯滑移和复合滑移时的受力和弯矩特性进行评估
已给出在公称竖向荷载作用下的纯滑移力和弯矩特性和转向刚度与垂直荷载的关系(参见图4.34a,b)。问题表述如下:
1. 确定原始曲线,即在名义荷载下系数和的值。忽略垂直和水平位
移。用公式(4.49)表示纵向力、侧向力和弯矩。考虑图4.9并使用公式(4.52,53)和(4.56)。绘制结果曲线。
图4.34a 纯粹打滑时的原始轮胎力特性(练习4.2)
图4.34b 转向刚度和初始弯矩特性(练习4.2)。
- 对于2000,4000和6000N,且 ,当时计算并绘制纯滑移曲线图。使用相似方程(4.21-26)。
- 对于6000N,且,,并在两个滑移角2°和8°的条件下绘制联合滑移曲线和。纵向滑移的从-1至 1取值。使用方程(4.27-29)和(4.35-40)。
第五章
非稳态轮胎模型
5.1 介绍
轮胎的瞬态和振荡动态特性将在这一章和后面的两章中讨论。本章致力于轮胎作为一个整体组成部分的模型开发。拉伸弦模型被选为平面外(反对称)行为的物理描述的基础。该模型显示了有限的接触长度,允许研究短波长现象。该模型结构简单,集胎体柔度和接触片滑移特性于一体。为了对偏航变化的力矩响应,需要引入接触块的有限宽度,这是通过连接到弦来实现的,即只考虑前后胎面单元柔度的毛刷模型。在更先进的字符串模型中,添加的胎面元素也可以转向侧面。这个更复杂模型的行为预计会更现实。当车轮在起伏的路面上行驶时,对恒定滑移角的侧向力的处理尤其明显。轮胎的惯性是重要的,当运行在较高的速度(陀螺夫妇)和横向和偏航激励频率不能再被认为是小。将讨论运动学和动力学模型的几种近似。第6章将理论应用于车轮摆振现象的分析。在第7章中,该模型将被简化为单点接触模型,该模型限制了应用于长波长的情况,但允许将应用扩展到纵向和组合的瞬态滑移情况。第9章讨论了更复杂的模型,包括有限接触长度、胎体柔度和传动带惯性效应的近似表示。这个更通用的模型能够考虑面外和面内轮胎的动态行为,可以扩展到非线性滑移范围,也在相对较短的波长。此外,还包括翻车路面不平。
5.2. 早期研究回顾
在描述轮胎水平非稳态行为的理论中,可以发现两个理论发展趋势。一组作者假设胴体具有弯曲刚度,另一组作者的理论基于弦的概念。
原则上,弦理论是简单梁理论,自与字符串模型最重要的点的挠度独自决定的道路给车轮的胎面运动,而与梁模型最重要的一点的斜率也必须被考虑作为一个额外的变量。后者导致系统的顺序增加了1。
Von Schlippe(1941)提出了著名的滚动轮胎运动学理论,并引入了拉伸弦模型的概念。首次考虑了有限接触长度。在同一篇论文中,迪特里希将这一理论应用于摆振问题。后来发表了Von Schlippe和Dietrich (1942,43)的两篇论文,其中也考虑了接触面积宽度的影响。考虑了两个刚性连接的同轴车轮,它们都近似于一维弦模型。弦及其弹性支承在周向上也应具有弹性。
Segel (1966)推导了一维弦模型的频响特性。同样的弦模型,Sharp和Jones(1980)开发了一种数字模拟技术,能够生成精确的模型响应。在此之前,Pacejka(1966)使用一台模拟计算机和磁带录音机(作为一种存储设备)来进行模拟,模拟的依据是出色的Von Schlippe近似,其中接触线被一条连接两个端点的直线近似。
Smiley(1958)提出了一个类似于von Schlippe(1941)的一维理论的总结理论。
Pacejka(1966)推导了具有胎面单元的有限宽度字符串模型的非稳态响应。介绍了轮胎惯性对陀螺效应的重要影响,讨论了轮胎局部滑动的非线性特性。介绍了轮胎理论在汽车摆振运动中的应用。在Pacejka(1972)中,通过对带质量的滚动拉伸轮胎模型行为的精确分析,研究了轮胎质量的影响。这个复杂而繁琐的理论不适合动态车辆的研究,然后是一个近似更方便的理论(Pacejka, 1973 a)考虑惯性力只在沿轮胎周长分布的一倍谐波。本章将给出理论概要和实验结果。
罗杰斯派生实证微分方程(1971)后来被赋予理论基础(1972)。由于美元罗杰斯轮胎的研究,振动响应在低频率范围内(质量效应不包括!)可以令人满意地描述,而高频率(短波长)减少了使用简单的二阶微分方程。
Sperling(1977)对滚动弹性车轮的不同运动学模型进行了广泛的比较研究。最近,Besselink(2000)调查和许多有趣的同期相比模型(冯·Schlippe·莫兰笑脸,罗杰斯Kluiters,铁达尼Pacejka)的频率响应函数和应对侧滑步,路径曲率(滑)和偏航角,和判断他们的表演也与振动现象。
Sekula等人(1976)从随机滑移角输入测试数据推导出了在0.05到4.0 Hz范围内的传递函数。根据这一信息,推导出子午线轮胎和斜交轮胎在滑移角阶跃输入下的转向力响应。Ho和Hall(1973)进行了一项令人印象深刻的实验研究,使用相对较小的飞机轮胎,在一个120英寸的研究道路车轮上进行测试,最高的摆动偏航频率为3Hz。与理论结果的临界相关研究表明,利用理论函数可以实现实验频响曲线的合理拟合(5.32,92,93)以下。应该指出的是,在测试小型轮胎的某些相似规则,如Pacejka (1974),应该遵守。
全面试验轮胎频率响应测试已经进行了一些研究人员,例如通过Meier-Dornberg 20Hz的偏航频率。后者的一些调查报告由Strackerjan(1976)进行了报告。研究人员开发了一种动态轮胎模型相比,基于不同的造型理念Pacejka描述的模型(1973)和讨论以后。两种模型都显示出与测量行为的良好一致性。Strackerjan所采用的直接方法与第9章所采用的方法类似。
在1977年Fritz报告了一项关于径向力和侧向力的广泛的实验研究,以及在车轮的不同的恒定偏航(侧滑)角下对垂直轴向振动的调直扭矩响应。并确定了侧向力和弯矩的平均值。早些时候,麦特卡尔夫(1963)进行了小型轮胎试验,Pacejka(1981)使用提供弹性胎面单元的教弦轮胎模型得出了平均转向刚度的理论结果。Laerman(1986)对汽车和卡车轮胎进行了广泛的测试,并将结果与理论模型在平均侧力、调直扭矩和频率响应特性方面进行了比较。该模型包括轮胎质量(基于Strackerjan, 1976),允许胎面元素相对于地面滑动。高桥等人(1987)也对汽车轮胎进行了类似的实验。他们开发了一个相对简单的数学模型,适用于车辆动力学研究,包括在不平的道路上转弯(参看第8章)。
2000年,Maurice发表了超过60Hz的实验数据,并在第9章中讨论了动态和短波长的非线性模型的发展。该模型与Zegelaar (1998, 参看第9章)的平面内动态模型相连接,形成了一种通用的组合滑移模型与神奇的公式,稳态函数推导在第4章。
轮胎行为的另一个方面是对轮拱变化的非稳态响应。Segel和Wilson(1976)发现,对于一个特定的摩托车轮胎,在弯曲角度上的一个步骤改变之后,大约20%的最终达到的侧力会立即对这个输入做出反应。其余部分的响应方式类似于侧向力对滑移角阶跃变化的响应,尽管松弛长度较大。Higuchi(1997)在弦模型的基础上对曲面的非线性响应进行了综合研究,实验评估了曲面角度逐步变化的响应。在第七章中,将讨论对曲面变化的响应。
下一节将在拉伸弦模型的基础上讨论反对称轮胎非稳态和动态特性理论的要点。
5.3 拉伸弦模型
如图5.1所示,轮胎模型由一根(通常是无止尽的)弦组成,该弦通过均匀的径向力分布保持一定的预紧力(与实际轮胎的充气压力相当)。在轴向,弦相对于轮毂中心平面有弹性支撑,但不能沿圆周方向运动。这根绳子在有限的长度内与水平的平坦路面相接触。假设弦的剩余自由部分保持其圆形(侧视图)。
该模型可由若干保持恒定相互距离的平行弦进行扩展。由于这种扩展,有限的接触宽度出现。弦被认为具有大量的弹性胎面单元,为了简化起见,假定这些胎面单元仅在圆周方向上具有挠性。根据上述假设,当轮轴受到偏航率时,轮毂中心平面两侧产生的纵向变形应该只由胎面单元承担。
图5.1 轮胎模型采用单筋拉伸,轮胎模型采用多平行筋拉伸,胎面单元在纵向上灵活。
为了使理论是线性的,我们必须限制自己的小侧向变形,并假设在接触区完全粘着。轮毂中心平面受侧向运动(侧向位移)和绕轴向运动(偏航角)的影响。这些动作构成系统的输入。激励频率用 表示。用表示空间或路径频率和接触点路径波长的假设恒定速度。所走的距离为。
可以考虑与车轮相对于道路的位置无关的替代输入量,但可以考虑其以滑移角和路径曲率或转弯滑移为特征的变化率。力 和力矩 从地面作用于地面上轮胎在轴方向和 轴方向分别形成对强加的车轮平面运动的响应。
图5.2 偏转胎面带单元的横向平衡
5.3.1 模型发展
为了得到弦的横向挠度v的表达式,我们考虑了如图5.2所示的胎面带单元的横向平衡。元素是全胎面宽度和包含元素的平行字符串与橡胶之间。在横向()方向上,作用在长度和宽度单元上的力的平衡结果为:
式中,为单位长度的侧骨架刚度, 为作用在弦组上的总拉力的周向分量(x方向)为作用在橡胶基体上的胎面带截面上的剪切力。设剪力为剪切角的线性函数,根据公式:
引入有效总张力,由式(5.1)可得:
图5.3单弦模型的俯视图及其相对于框架的位置
在轮胎没有与路面接触的部分,接触压力消失,因此 并且
如果参数 相同,则具有多个平行弦的模型和具有单个弦的模型的横向行为是相同的。图5.3给出了单弦模型的俯视图。图中表示了长度 ,即松弛长度。松弛长度等于:
随着这个量的引入,对于字符串的自由部分,Eq.(5.4)变为
如果我们认为轮胎的周长比接触长度长得多,我们可以假设,后缘的挠度 对前缘的挠度 的影响可以忽略不计。自由弦在接触区附近的挠度可以分别认为是弦在前缘和后缘挠度的结果,而不是
图5.4 字符串模型的两个连续位置。前缘和后缘的滑动消失区域以及滑动速度 和摩擦力的相容性需要保持一种可能的扭结,而这种扭结显然只能存在于后缘(2)
两者的结合。这些各自区域的偏折现约为:
考虑简化边界,构成式(5.6)的解。条件是,对于较大的 ,挠度趋于零。在 处, 分别是斜率:
由于我们没有考虑在接触区滑动的可能性,在从自由范围到接触区的过渡点处,扭结可能以变形的弦的形状出现。这似乎是一个逻辑上的假设,通过滚动过程,弦在前缘周围形成一个连续变化的斜坡,而在后面,由于没有弯曲刚度,斜坡可能会发生不连续。下面是对这句话的一个很好的证明。考虑到在过渡点处滑动消失区域的观测,参照图5.4。为了保持一种可能的扭结,绳子上一点相对于路面的滑动速度方向和路面施加在绳子上的摩擦力在尾缘是相互兼容的,而在前缘则是不兼容的。因此,必须得出这样的结论:扭结只可能出现在接触线的后缘。因此,前缘(5.8)处的斜率方程可改写为:
这个方程对最终挠度的表达式的字符串的发展构成重要关系,稍后我们将看到。
在 第二章我们已经得到的一般微分方程的纵向和横向滑动速度滚动身体受到横向滑动和旋转。这些方程(2.58.59)变成了我们假设的滑动速度为零的情况:
在这些方程中, 表示车轮中心(或更好的说法是接触中心)和 和 所走的距离,所考虑的粒子相对于处于水平未变形状态的运动轴系统 的坐标。
这些偏微分方程将用拉普拉斯变换来解。转换将用大写字母书写。这个变换不是对时间进行的,而是对 所走的距离进行的,这里速度 假设为常数。变量的拉普拉斯变换,一般用
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[238817],资料为PDF文档或Word文档,PDF文档可免费转换为Word


