
英语原文共 12 页,剩余内容已隐藏,支付完成后下载完整资料
喷丸残余应力的模拟
K.Schiffner*, C. Droste gen. Helling锡根大学工程力学与控制工程研究所,保罗 - Bonatz-STR。 9-11,Fachbereich 11,Maschinenstechnik,D-57076,Siegen,德国
摘要:喷丸处理是一种冷加工工艺,其中称为弹丸的小球形部件以高达100m / s的速度喷射在金属工件的表面上。因为残余压应力的产生,这种处理会使得疲劳性能得到提升,同样因为冷加工效果,会使得表面硬度得到提升。这篇文章的目的是借助有限元方法模拟这一过程,以根据参数预测残余应力的变化,大小和分布,例如,喷射速度,喷射直径和材料参数。在第一步中,使用轴对称模型来模拟弹性球对弹塑性表面的垂直碰撞。由于塑性变形较大,使用9/3混合配方元素代替普通的不太适合这项任务的九节点位移配方元素。第二步显示了轴对称方法的结果如何转化为三维模型,以便研究相邻撞击的效果。 #1999爱思唯尔科学有限公司保留所有权利。
1.简介
通常在技术实践中,工件的外层是应力最高的区域。 因此,已经开发了许多机械,化学和热处理以改善工件表面的机械特性,以便增加例如工件表面的疲劳寿命。 其中一种机械方法是喷丸。 喷丸处理是一种冷加工工艺,其中球形部件流喷射在弹塑性工件上。 这个过程可以被看作是弹丸对工件多重地和持续的重复性撞击。 在每次冲击下,工件在弹丸撞击工件时产生局部塑性变形。在弹丸反弹之后,工件的弹性变形部分膨胀并推动塑性变形的部件,这导致产生残余压应力。 通过反复逐步处理工件的整个表面,所有冲击产生的残余应力分布随深度而变化,但前提假设是在水平方向上撞击几乎均匀。
喷丸过程的主要参数是:
(1)弹丸的半径r
(2)弹丸的初始速度v
(3)弹丸材料性能HVs和工件材料性能HVw
(4)工件的厚度
(5)覆盖或曝光时间
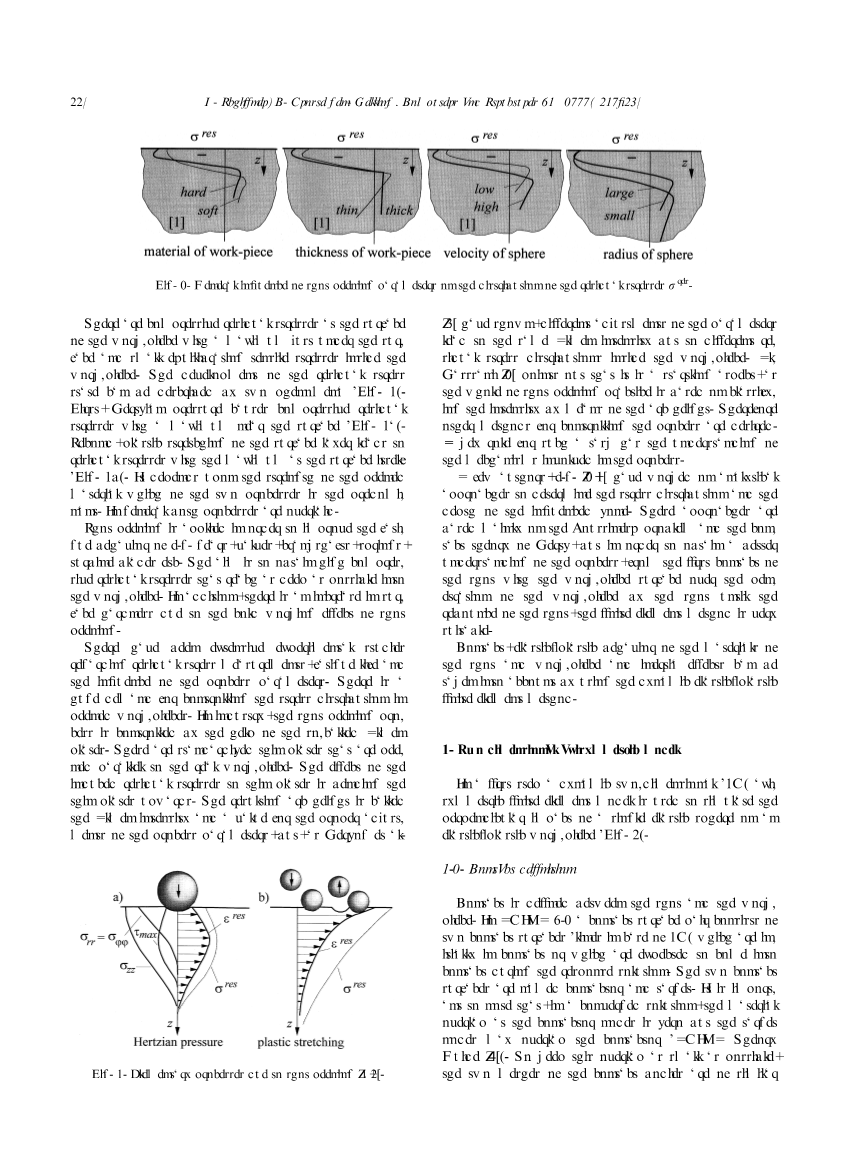
从实验数据中获得的,一些参数对残余应力分布的一般影响如图1所示
图1.喷丸参数对残余应力分布的一般影响
工件表面存在残余压应力,在表面下方存在最大压应力,并且在工件内部产生小的平衡拉应力。 残余应力状态的发展可以用两种现象来描述(图2)。 首先,赫兹压力会在表面附近产生最大的残余压应力(图2a)。 其次,表面层的塑性拉伸导致在表面本身具有最大残余应力(图2b)。 这取决于喷丸材料的强度,这两种工艺中的哪一种是主要的。 通常这两个过程都是重叠的。
喷丸处理是为了改善疲劳性能,例如齿轮,阀门,曲轴,弹簧,涡轮叶片等。目标是获得尽可能深入工件的大的残余压应力。 此外,由于喷丸硬化的冷加工效果,表面硬度也会增加。
已经有关于残余应力大小,疲劳寿命和工艺参数的影响的广泛的实验研究。 控制喷丸工件的应力分布有巨大的需求。 在工业中,喷丸过程由所谓的阿尔门板块控制。 这些是标准化的薄板,与真实工件平行喷丸。 残余应力对薄板的影响是向上弯曲薄板。由此产生的弧高被称为阿尔门强度和适当调整工艺参数的值,但正如Herzog等人已经表明,参数的不同调整导致相同的阿尔门强度,但导致工件内部的不同残余应力分布。 Al-Hasssani指出,这是一个令人吃惊的方面,因为整个喷丸强化实践的基础是通过弧高来分类强度。 因此需要用于控制该过程的其他方法。这一任务的关键步骤是理解过程中涉及的机制。
图2. 喷丸的初级过程
一些作者,例如[1,2]研究分析方法来确定应力分布和影响区的深度。这些方法主要基于Boussinesq问题和Hertz的接触理论,但为了更好地理解该过程,从工件表面与工件表面的第一次接触,直到弹丸的反弹,这种有限元法非常适合。
通过使用动态弹塑性有限元方法,可以考虑接触,弹丸和工件材料的弹塑性行为和惯性影响。
2.二维轴对称模型
在第一步中,使用动态二维(2D)轴对称有限元模型来模拟单个弹性球对弹塑性工件的垂直碰撞(图3)。
2.1接触定义
触点和工件之间的接触是固定的。在ADINA 7.1中,接触面对包含两个接触面(在2D情况下为线),它们最初接触或预期在响应解决方案期间接触。两个接触面被称为接触器和目标。 需要注意的是,在融合解决方案中,接触器节点处的材料重叠为零,但目标节点可能与接触器重叠(ADINA Theory Guide [5])。为了保持这种重叠尽可能小,接触体的两个网格是相似的。必须防止工件的节点穿透射击,因为工件中产生的应力更受关注。出于这个原因,射击被定义为目标,并且工件被定义为与感知相反的接触器。
图3. 轴对称有限元模型的离散
2.2积分方法
描述动态系统行为的动态运动方程必须通过一个积分方案来解决。工件与工件之间的接触条件耦合的控制方程如下:
对于弹丸
对于工件
由于Al-Obaid [6],阻尼可以忽略不计。
对于控制运动方程的解决方案,使用隐式Newmark方法。Newmark方法[7]提供了最小的数值误差。在测试计算中,与中心差分方法和Wilsonplusmn;Y方法相比,该方法显示出最佳行为。
一般来说,只有结构动力学问题中的最低模式才会受到载荷向量的激励。高级模式对结构行为的影响可以忽略不计,因此有限元素不需要精确地表示这些更高的频率。在喷丸强化作为一种高度动态的过程中,更高的模式也会被激发,从而消除响应。因此,将这些高模式响应从解决方案中移出是合理的。Newmark方法通过调整两个参数d和a来引入人工阻尼,这两个参数必须满足以下条件才能保证方案的无条件稳定性:
使用无条件稳定积分方法,与中央差分积分方法等条件稳定积分方法相比,可以使用更大的积分时间步长。设定d = 0.75,因此a = 0.390625可以提供较高模式的良好数值阻尼和解决方案的充分准确性。将这些参数应用于两个桁架的影响模型已经与解析解方案表现出了非常好的一致性,并且显示了在这种影响问题的情况下,这种集成方法优于其他集成方法的优势。
2.3元素类型
由于隐式时间积分法和高预期应变,使用高阶轴对称元素。在接触区域或大应变区域,使用9/3混合配方元素。当一个弹性的plusmn;塑性材料进入大塑性区域时,它将变得几乎不可压缩,纯粹的基于位移的塑性元素不具有足够的有效性[7]。在这种情况下,由位移导数得到的体积应变非常小。导数不如位移准确,因此体积应变中的任何误差都会导致应力出现大的误差。除了基于纯位移元素的位移插值之外,压力也被插值在混合元素中。因此,位移和压力是解决方案变量,但它们并不相互独立,因此压力变量可以静态压缩。在ADINA中,实现了用于二维计算的9/3混合单元,该单元实现了双二次位移插值和线性压力插值。
3.模型验证
在第一步中,模型将与一些分析和实验解决方案进行比较,这些解决方案和实验解决方案可用于半球体固体球体的弹性和弹塑性冲击。
3.1弹性解决方案
由于Al-Hassani [1]有一个解析解决方案,接触时间和弹性球的单个垂直碰撞(半径r)对同一材料的半固体固体的平均接触压力。该解决方案基于赫兹接触理论。
平均接触压力:
接触时间:
其中rho;=球体和固体的密度,E =杨氏模量,mu;=泊松比,v =球体初始速度,r =球体半径。
值得注意的是,平均接触压力不取决于球体的半径。有限元计算是针对钢铁进行的。有限元解决方案的平均接触压力可以通过两种不同的方法来计算。首先,可以用p(r)的多项式对接触压力的分布进行插值,并且可以将得到的方程相对于接触半径a进行积分。这个过程对于接触半径非常敏感,这很难以足够的准确度获得。第二种方式是指赫兹解,其中平均压力p等于在接触区域中心出现的最大压力p0的2/3。由于以上给出的方程式,有限元计算和解析解之间的偏差为接触时间的2.3%和平均接触压力的5.3%(积分)或1.6%(2/3 p0)。
接触时间和平均压力的分析和数值解决方案之间的一致性非常好。球体半径和速度变化的趋势也得到了很好的再现。分析结果和FE方法之间的差异可以追溯到能量损失由于应力波而引起的事实,这些应力波都包含在有限元解中。撞击后球体的速度小于其初始速度。此外,解析解决方案不考虑球体对工件的压痕。
为了获得更好的赫兹解,对于比目标更强的球体重复这些计算。图4给出的FE解的归一化应力与Hertz得到的解的结果非常一致,见图1.在图4中,示出了作为主应力的沿着旋转轴的应力。应该指出的是,最大剪切应力在表面下是最大的。塑性变形首先发生在表面以下的这一点,并且当球进一步进入目标时,塑性变形区将生长并延伸到表面。
图4. 垂直中心线的标准化应力vs标准化深度(有限元)
3.2弹塑性解决方案
首先使用上面介绍的有限元模型模拟一些实验发表的数据。事先必须解决的问题是获取给定工件的有限元方法所需的材料数据。在喷丸强化练习中,通常只说明工件材料和射击的硬度。没有关于材料的应力 - 应变曲线的数据,甚至没有给出关于屈服极限的数据。另一个重大问题是该过程涉及的极高应变率。关于极短的接触时间(大约1times;10^6s),很明显应变率非常高。在文献中,冲击过程中的应变率的值是以平均值的形式给出的10^4l/s。Hornauer [8]在接触时间的第一个时间内给出了约2times;10^5l/s的平均值。有了上述有限元模型,在单个时间步长内,这个数就会增加到3times;10^6l/s。大多数材料测试数据都是指应力-应变曲线,应变速率约为上述速率的1/100。 此外,ADINA不提供2D固体元素的应变速率敏感材料。
为了了解使用有限元方法来模拟喷丸过程,应变率对材料行为的影响被忽略了。将来,还必须找到一种方法来考虑这些影响。
为了验证喷丸参数对下面给出的特征量的影响,正在进行三个参数射击半径r,工件材料和球体的初始速度v0变化的计算。
假设是无摩擦的接触和钢球的始终弹性行为。
图5中给出的计算和检验的数量是:
1.最大压痕深度wmax。
2.压痕残余深度wres。
3.塑性区域zp的深度。
4.表面处的残余径向应力。
5.最大残余径向应力s resmax。
6.最大残余径向应力深度zmax = z(sresmax)。
7.接触半径a。
工件的两种材料已被考虑在内。第一个是42CrMo4钢,它的喷丸粒子的初始速度高达100米/秒,0.20plusmn;1.0毫米半径。另一件工件54CrSi6钢的参数与42CrMo4的速度相同,但只使用一个0.25毫米半径的喷丸材料。
图5. 调查数量的定义
图6. 有限元方案的实验结果对比
这种选择的原因是42CrMo4钢的残余压痕和接触半径a的不同半径r和球体初始速度v0的实验结果存在[9]。在该参考文献中,钢的硬度为296HV10,准静态载荷的合适的应力-应变曲线在文献中给出。[10]
图7. 不同参数的计算结果
图8.残余应力的计算
高强度钢54SiCr6的应力-应变曲线是由Sommer [11]提供的,由于可以使用喷丸硬化处理,他可以测量残余应力。两种应力-应变曲线均通过多线性塑性材料定律近似。
从[9]进行的实验研究获得的结果与从有限元分析得到的结果的比较如图2所示。
可以看出,残余压痕的数值结果和接触半径a与实验结果非常吻合。小球半径的巨大差异可以追溯到这些小值的测量失败相对较高的事实。由于使用了基本的物质法,这些结果非常令人鼓舞。
在图7中,显示了上述参数结果的示意图。为了使差异明确,一些图表上的比例尺得到了增强。左图的灰色表面代表右边的整个区域。
在图8中示出了材料54SiCr6的残余应力的带状图。其他参数是r = 0.25mm的球体半径和v0 = 60m / s的初始速度。计算得到的最大残余应力深度与Sommer [11]针对相同参数所获得的实验结果非常吻合。但最大的实验结果只有计算结果的60%。差异的主要原因如下:
·计算出的残余应力是单次冲击的结果,而不是实际喷丸过程中大量冲击工件的冲击。
·将计算出的沿着对称轴的应力分布与作为平均分布测量的实验数据进行比较。
另一方面,应力带图的过程(图8)与Mori等人的结果在定性上非常一致。[12,13]。用可比较的有限元模型计算出的最大残余径向应力也达到了喷丸材料的极限强度。只能使用3D模型而不是轴对称2D模型来模拟相邻镜头。
4.三维模型
为了减少问题的大小,接触问题和动态影响被消除。这个想法是只考虑冲击球体对工件的影响,并将其转化为一个准静态问题,其时间依赖性载荷函数可以更容易地解决。该方案如图9所示。
图9. 从二维模型到三维模型的转换过程
图10. 动力学和静力学残余应力计算的对比
图11. 考虑对称性的三维模型
在第一步中,对于每个计算的时间步,记录动态轴对称2D模型的每个表面节点(z = 0)的两个方向r和z上的位移ur和w。结果获得了函数ur(r,t)和w(r,t)。代表规定位移的时间函数的位移ur和w可以使用多项式变换为任意表面节点的位移ux(r,t)和uy(r,t)。
这些位移被施加到梁的另一端与接触半径范围内的工件连接的一端。 通过使用ADINA的tdeath选项,可以从模型中取出这些元素,从而可以计算上一个时间步骤中的残余应力。 在轴对称二维模型的情况下,这一过程导致残余应力完全相同,计算时间显着减少。
此外,可以减少所需模型和元件的尺寸,而不会损失太多精
全文共8263字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[11811],资料为PDF文档或Word文档,PDF文档可免费转换为Word


