
英语原文共 26 页,剩余内容已隐藏,支付完成后下载完整资料
对一致拓扑体积参数化的复杂对象的等几何计算重用方法
摘要
体积样条参数化和计算效率是等几何分析中的两个主要挑战,为了解决这个问题,我们提出了一个计算重用的框架对一组具有相似语义特征的三维模型进行等几何分析。给定一个模板域,基于B样条的一致体积参数化首先为一组模型构建类似的语义特征。 我们的框架研究了一种高效的无正交方法通过B样条提取和多项式近似来计算刚度矩阵。在我们的方法中,刚度矩阵的评估和边界条件的施加可以在一组CAD模型的等几何分析期间被预先计算和重新使用。为了显示我们的方法的有效性,提出了具有复杂几何形状的示例,并且可以实现类似于线性有限元分析中的计算的效率,以对一组模型进行等几何分析。
关键词:计算复用; 等几何分析; 等体积参数化
1.简介
休斯等人提出的等几何分析方法,提供了一种将计算分析和几何设计的无缝集成的可能性。目前IGA发展的两大挑战是体积参数化和计算效率。 在最近的Cottrell和Hughes的书中已经指出,等几何分析最重要的挑战是如何从给定的CAD模型构建适合分析的参数化。另一方面,通常采用高阶基函数来获得高度连续性的平滑解,而这又增加了填充刚度矩阵时的计算成本。 在本文中,我们提出了一种在具有相似语义特征的三维模型上对IGA进行计算重用的方法,从而可以显着提高计算效率。 可以从这项研究中受益的计算设计应用包括:1)具有相同拓扑结构但形状不同的产品系列的物理分析; 2)用作基于物理形状优化的内部循环,其中在第一次应用完整的IGA之后可以大大加速计算迭代。应该指出的是,IGA解的结果不能通过具有相似语义特征的模型之间的一致参数化(例如,[11,12,14,21])的映射直接重用。如图1(a, b)和(c,d),均匀边界的热传导问题和下面的源函数。
f(x,y) = minus;2pi; 2 sin(pi;x)sin(pi;y)
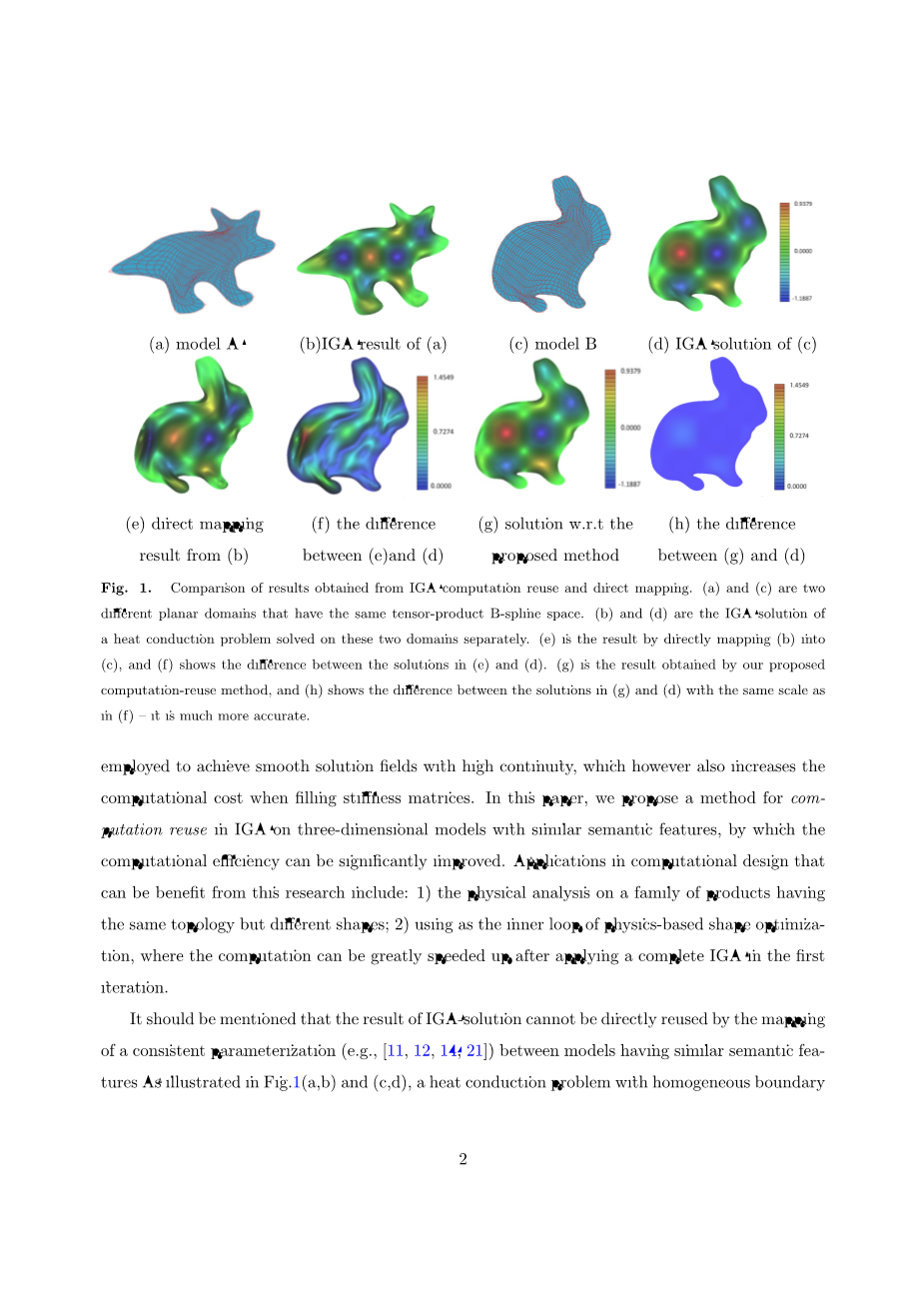
分别在具有相同张量积B样条空间的两个不同平面域上求解。 当将图1(b)的结果直接映射到(c)的区域时,热分布的结果如(e)所示,这与IGA结果(即图1(d))完全不同。 图1(f)显示了(e)和(d)之间的颜色差异。 在其他方面,当使用本文开发的计算复用方法时,相应的解决方案如图1(g)所示,其中引入的近似误差是微不足道的 - 查看图1(h)所示的颜色差异。
图1. 从IGA计算重用和直接映射获得的结果比较。 (a)和(c)是两个不同的平面域,它们具有相同的张量积B样条空间。 (b)和(d)分别是解决这两个域的热传导问题的IGA解。 (e)是直接将(b)映射到的结果(c)和(f),显示了(e)和(d)中解决方案之间的差异。 (g)是我们提出的计算重用方法得到的结果,(h)显示了(g)和(d)中解与(f)中相同比例的差 - 它更准确。
我们工作的主要贡献可以概括如下:
bull;提出了一种有效的无正交方法,用B样条提取和多项式逼近技术应用于三变量有理B样条函数来计算刚度矩阵。
bull;我们提出了IGA中的计算重用框架以及在此框架中施加边界条件时的重用方法。 对于大量自由度(DOF)的问题,使用我们的方法可以观察到12.6倍的加速。
本文的其余部分安排如下。 在第2部分中,将回顾关于IGA的体积参数化和计算效率的相关工作。 第3部分介绍了构建一致的基于B样条的体积参数化的方法。第4部分介绍了使用B样条提取和多项式近似技术的无正交IGA方法。 通过结合第3和第4部分中介绍的技术,第5部分给出了一组具有相似语义特征的模型的计算重用框架。最后,我们在第6部分中总结本文并讨论中可能的未来工作。
2.相关工作
体积参数化 从图形应用的角度来看,3D模型的体积参数化已经在[15,28,29]中进行了研究。 另一方面,在IGA的文献中也有一些关于体积参数化的研究。 Martin等人 [17]提出了一个方法根据离散的体积谐波函数通过B样条体积参数化来拟合0类三角网格。Aigner等人提出了用于构建扫掠体积的NURBS参数化的变分方法。[1]。 Escobar等人 [6]提出了一种方法,通过使用自适应四面体网格化和网格解离技术来构造复变类型零固体的三变量T-spline体积。 Zhang等人 [33]提出了一种稳定和有效的算法,用于从边界三角形构造属于零几何的内射固T样条。基于莫尔斯理论,[26]中提出了一种具有任意拓扑的网格模型的体参数化方法。 在[31,32]中,提出了一种约束优化框架来获得分析适合的计算域的平面和体积参数化。Pettersen和Skytt提出了样条体积法,以获得等质量应用的高质量体积参数[19]。 Zhang等人 [34]研究了由八叉树结构和边界偏移从边界T样条表示构造共形实体T样条。 对于具有同胚拓扑的三流形实体模型的体积参数化,Kwok和Wang [13]提出了构建具有一致拓扑的体积域的算法。 生成的体积参数化共享相同的基本域集合,并受到锚点形式的相应语义特征的约束。 本文提出了一种紧支撑的径向基函数方法,为具有相似语义特征的模型构造一致的体B样条参数化。
等几何分析的效率问题 高阶基函数用于表示IGA中的几何和物理场,以实现高精度的模拟结果。 因此,计算效率是等几何分析领域的关键问题。 为了提高效率,已经提出了几种方法。 有一种趋势是使用图形拥有单元(GPU)来提高组装刚度矩阵的计算效率(例如,[10])。 另一方面,对积分计算的效率改进也进行了研究。 休斯等人[9]提出了一种基于NURBS的等几何分析的有效正交规则。Antolin等人[2]基于样条和NURBS形状函数的张量积结构,开发了一种总和分解方法来显着节省正交计算成本。 Mantzaflaris和Juuml;ttler[16]提出了一种基于Galerkin的等几何分析的插值和查找表的无正交积分方法。 在本文中,我们提出了计算重用的概念,以提高IGA在具有一致拓扑的一组CAD模型上的效率。
图2. 给定模板基本域Psi;和目标表面模型M,可以应用表面交叉参数化[11]将M一致地划分到Psi;的表面。 在通过将M映射到Psi;获得表面模型Psi;M之后,将Psi;M和M上的顶点用作句柄,以通过体积参数化将内部片上的采样点映射到M [24]。 M的B样条实体可以通过将其拟合到边界表面和M的采样点来获得。
3.复杂三维模型的一致B样条体积参数化
为了准备IGA中的计算重用,我们需要将模型划分为一组与预定义的基本域一致的基本域,其中每个基本域将由三元样条表示。 我们假设将IGA的重用应用于具有相似语义特征的模型,例如具有不同形状但具有相同拓扑的产品的整个序列。 分析将考虑指定为锚点的语义特征,使得边界条件也可以被重用。
给定体积基域(Psi;)的连通性,例如图2中的模板基域,我们可以将目标表面模型(M)划分为一组与Psi;一致的体积子域。边界曲面首先被划分 一致地根据锚点[11,12],并且边界表面被用作约束来使用基于CSRBF的弹性函数来构建体积参数化。 体积参数化用于将Psi;的内表面上的采样点包装为M.通过将M的边界表面和采样点拟合在上述确定的内表面上,在每个域中构造三元样条实体。
3.1 一致的边界表面分解
基于M上指定的锚点,使用[11,12]中的方法根据Psi;中的节点一致地划分M的表面。 其基本思想是追踪Psi;边界面上每个边的M上锚点之间的最短路径。 为了确保拓扑一致性,我们需要确保路径在追踪路径时没有交点,阻塞和错误的循环顺序[20]。 然后可以通过该分区计算表面交叉参数[11,12],并且通过将M的边界表面映射到Psi;来获得表面模型Psi;M。一旦边界表面被分割,下一步就是构建内部补丁。
3.2 基于CSRBF的体积参数化
由于M是没有体积信息的表面模型,我们需要构建M的内部贴片。首先对Psi;中的内部贴片进行取样。 通过[24]中提出的体积参数化,使用Psi;M和M上的顶点作为手柄,可以将Psi;的内部斑点上的采样点映射到M的内部。具体地说,体积参数化可以用弹性函数:
, (1)
其中v j s是Psi;M上约束顶点的位置,d j s是权重,P(x)是考虑f的线性和常数部分的线性多项式。
为了求解满足约束条件的d j的集合,v 0i= f(v i ), 我们可以用(1)式的右边替代弹性函数f(v i),得到
(2)
由于该方程相对于未知数dj s和P(x)的系数是线性的,所以可以将未知量表达为线性系统并将其求解。
我们将Wendland的紧支撑径向基函数定义为phi;(r),它由下式给出
其具有半径为lambda;的紧凑支撑并具有连续性。 由于使用了紧凑的核函数,线性方程组将变得稀疏并且可以通过Cholesky分解或LU分解来有效地解决。
现在体积参数化已经建立。 Psi;内部斑点上的采样点通过f(·)映射到M上。
3.3.B样条实心结构
通过将S(u,v,w)的边界面拟合到其对应的边界面上,可以构造M内每个基域的三元样条实体S(u,v,w)(即我们实现中的B样条) 对M和由非线性弹性函数f(·)得到的内部采样点。 通过这种方式,我们可以将目标模型M转换成一系列具有一致拓扑结构Psi;的连续三元样条实体。 当将其应用于模型序列{M i}时,所有模型将具有相同连通性但不同控制点(即不同形状)的样条实体。在此设置的帮助下,我们将演示如何重用在其他模型的IGA中对一个模型采用的IGA计算。
4.利用B样条提取和多项式逼近进行无正交等几何分析
在本节中,我们提出了一种高效的无正交方法,用B样条提取和三元有理B样条函数的多项式逼近技术来计算刚度矩阵的条目。 在这里我们使用热传导问题作为例子来演示我们的方法的功能。 无正交方法可以应用于许多其他计算物理问题,例如固体力学中的线性弹性问题。
4.1. 关于伯恩斯坦多项式的初步讨论
伯恩斯坦多项式的一些初步将用于我们的方法。 他们在下面进行评论。
引理4.1. 伯恩斯坦多项式的积
引理4.2. 伯恩斯坦多项式的积分
引理4.3. 伯恩斯坦多项式的高程
命题4.4. 令R(u,v,w)和S(u,v,w)为参数函数
其中和是比例值。 那么R(u,v,w)和S(u,v,w)的乘积可以定义为
其中
这个命题可以由方程(4)直接证明。
4.2. B#39;ezier曲线提取B样条体积
为了实现有效的计算,用B#39;ezier提取[3]解决了等几何分析问题,其中逐段B-样条表示首先被转换成B#39;ezier形式。
定义在结矢量上的B样条基可以表示成伯恩斯坦多项式的线性组合,即
其中C(xi;)表示B#39;ezier提取算子,B(xi;)是在[0,1]上定义的伯恩斯坦多项式。 转换矩阵C(xi;)是稀疏的,它的入口可以通过结插入和递归计算获得。 B#39;ezier提取的细节可以在Borden[3]和Scott[22]等人的研究中找到。
利用转换矩阵C(xi;),C(eta;)和C(zeta;),B-样条体积的B#39;ezier提取可以表示如下
其中Q是B样条体积的控制点,P是提取的B#39;ezier体积的控制点,C(xi;),C(eta;)和C(zeta;)由(8)导出。 图3中示出了具有三次B样条体积的示例,以说明提取的四个具有不同颜色的B#39;ezier体积的提取结果和相应的控制格。
(b)在(a)中提取B#39;ezier体积的B样条体积
(a)立方B样条体积
图3. B#39;ezier提取示例
4.3. 热传导问题的等几何分析
给定具有边界Gamma;=part;Omega;D的域Omega;和体积参数化如下
我们将考虑以下热传导问题:
其中x是笛卡尔坐标,T表示温度场,施加温度为T 0的狄利克雷条件应用于part;Omega;D,g是用户定义的函数作为经典热传导方程的源项。
根据经典的变分方法,我们寻求Sobolev空间中的解H(Omega;),例如part;Omega;D上的T(x)=T 0(x)和
psi;(x)是试验函数。 通过部件整合并应用边界条件后,我们就可以获得
遵循IGA范式,温度场用三元样条基函数表示
其中B i函数是伯恩斯坦基函数,u =(xi;,eta;,zeta;)isin;P是域参数。然后,我们定义物理域中的试函数psi;(x)为
方程式中的弱形式 (11)可以写成
最后,我们得到一个线性系统,其系数矩阵类似于从经典有限元方法获得的刚度矩阵,例如
及
这里J是从物理域到参数域的转换的雅可比矩阵,K是雅可比矩阵的逆矩阵。
4.4. 刚度矩阵条目的显式表示
假设刚度矩阵的项由Mijk表示,,我们可以推导出以下命题。
命题4.5. F(u)可以表示为一个三变量有理B#39;ezier函数,如下所示
其中
其中J ijk具有如[27]中给出的以下形式:
及
根据公式(8)中命题4.4中两个三元伯恩斯坦多项式的乘积公式,我们可以将F(u)改写为一个高阶三元有理Bernstein多项式,
其中F ijk可以根据等式(7)计算。
在一般情况下,有理B#39;ezier函数在[0,1]上的积分要么非常复杂,要么没有分析解。 通常采用高斯正交法在通用IGA中近似计算式(13)中的有
全文共12612字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[11192],资料为PDF文档或Word文档,PDF文档可免费转换为Word


