用非圆齿轮合成分度机构
文章历史:
2015年12月9日接收 2016年6月15日收到修订表格 2016年6月20日接收 2016年7月6日在线可用
关键词:非圆齿轮行星齿轮系分度机构
摘要:分度机制是自动化机械中最重要的机制之一。 各种分度机构在应用中已经存在,包括凸轮机构,滑轮机构,间歇齿轮机构等。 本文采用行星式非圆齿轮系综合了另外一种特殊的分度机构,涵盖了三种不同类型的齿轮系。
在系统介绍了分度运动规律和三种非圆形行星齿轮系之后,合成了非圆形齿轮的齿轮比和俯仰面。 随后,利用计算机化设计和仿真三个例子,本文展示了这些机制的适用性。
1.介绍
分度机制用于实现间歇运动,应用于仪器,手表,投影机,排污机床以及印刷,包装和自动机械,输送线等。 存在各种分度机制,包括棘轮,擒纵机构,间歇齿轮,星轮,分度凸轮和日内瓦机构
鉴于古柯尔系统,棘轮齿轮被用于武器装备,而擒纵机构则在机械手表,电表和里程表上应用[4]。间歇齿轮是另一种广泛使用的分度机构,具有精确的齿轮比[5]。所有这些机制都面临着一个类似的冲击载荷问题,可以用特殊牙齿来解决。因此,星轮机制成立[1]。
同时,日内瓦机制广泛应用于自动化机械或输送线路。为了减少冲击载荷,应用了连杆,齿轮和凸轮的基本的日内瓦机构,如[6]所示。提高机构的动态性能和运动特性的另一种方法是使用曲线槽,如[7,8]中所述。
最近,由于承载能力高,噪音低,振动小,可靠性高等优点,凸轮机构分度应用最为广泛,特别是自动机械[9]。滚子齿轮凸轮机构,平行分度凸轮机构和滚筒分度凸轮机构是其三大类型[10]。已经对其几何设计[11-13],分析[14-16],测量[17]和扭矩平衡[18,19]进行了研究。
此外,非圆形齿轮的设计和制造取得重大进展,已经开发出非圆形齿轮的各种应用:弗格森[20]在位置域使用抛物线运动的非圆形齿轮,以实现直线运动速度域; Freudenstein和Chen [21]提出了用于自行车的变速比链传动; Emura和Arakawa [22]利用非圆形齿轮来分析转向机构; Han [23]提出了一种在平面非圆齿轮应用中完全平衡空间联动摇摆的方法; Dooner [24]使用非圆形齿轮来减少旋转轴中的速度和扭矩波动; Litvin等[25]研究了非圆形齿轮的齿轮传动,用于速度变化和功能的产生; Erika等人[26]分析了非圆形齿轮和凸轮跟随器系统作为函数发生器;胡等[27]分析了齿轮泵中使用的三级非圆形行星齿轮机构的俯仰曲线; H. Terada等[28]开发了具有非圆形齿轮和凹槽凸轮的可穿戴机器人的膝盖运动辅助机构; K.-H。 Modler等[29]提出了用非圆形齿轮合成齿轮联动的一般方法; Liu et al。 [30]设计了在光纤端面抛光机中使用的非圆形齿轮,以执行图8模式。 D.Mundo [31]开发了一种具有非圆形齿轮的行星齿轮系,用于高性能自行车的动力驱动机构的设计; Dooner [32]对包含日内瓦轮和齿轮系的机构进行了运动学研究,以便在运动开始时实现零加速度跳跃的间歇运动。
如上所述,可以应用非圆形齿轮来实现不同的运动,证明使用非圆形齿轮的分度机构的发展。事实上,这个想法最初由F.Cunningham提出,作为他与非圆齿轮的开创性工作的一部分。坎宁安使用行星齿轮系作为非圆形齿轮的相加装置,以实现分度运动,在驾驶原理和设计方法方面表现出独特性[2]。然而,仍然存在局限性:首先,在他的研究中,仅讨论使用外部非圆形齿轮的分度装置的情况,而不考虑斜面和内齿轮类型的其他可能情况。其次,坎宁安刚刚讨论了基本指数运动规律,使改进的指数运动规律保持不变。第三,与不同齿轮比分布相关的运动特性也没有讨论。
本文综合了非圆齿轮分度机构,不仅包括外齿轮类型,还包括内锥齿轮和锥齿轮;不仅研究了基本的分度运动,而且改进了分度运动;另外,不同步数的齿轮比设定均匀,讨论了运动特性。
此外,与日内瓦机构和分度凸轮机构相比,所提出的非圆齿轮分度机构具有以下优点:a)驱动元件为齿轮时,运动分度规律相当准确; b)分度角可以任意设计,而不是像在日内瓦机构和分度凸轮机构中等分360°; c)齿轮传动的接触比通常大于凸轮的接触比,带来更大的承载能力。 d)对于不同的齿轮类型,非圆形齿轮装置具有不同的配置,因此适合不同的工作和安装条件。
基于上述讨论,本文首先介绍了分度机构的运动规律,然后详细介绍了三种非圆形行星齿轮系,综合了非圆齿轮的齿轮比和齿面。最后,对三种分度机制的设计和仿真进行了说明,证明了其适用性。
2.分度机制运动规律
一般来说,分度机制有两种类型的运动:基本间歇运动(BIM)和改进的间歇运动(IIM)[9]。
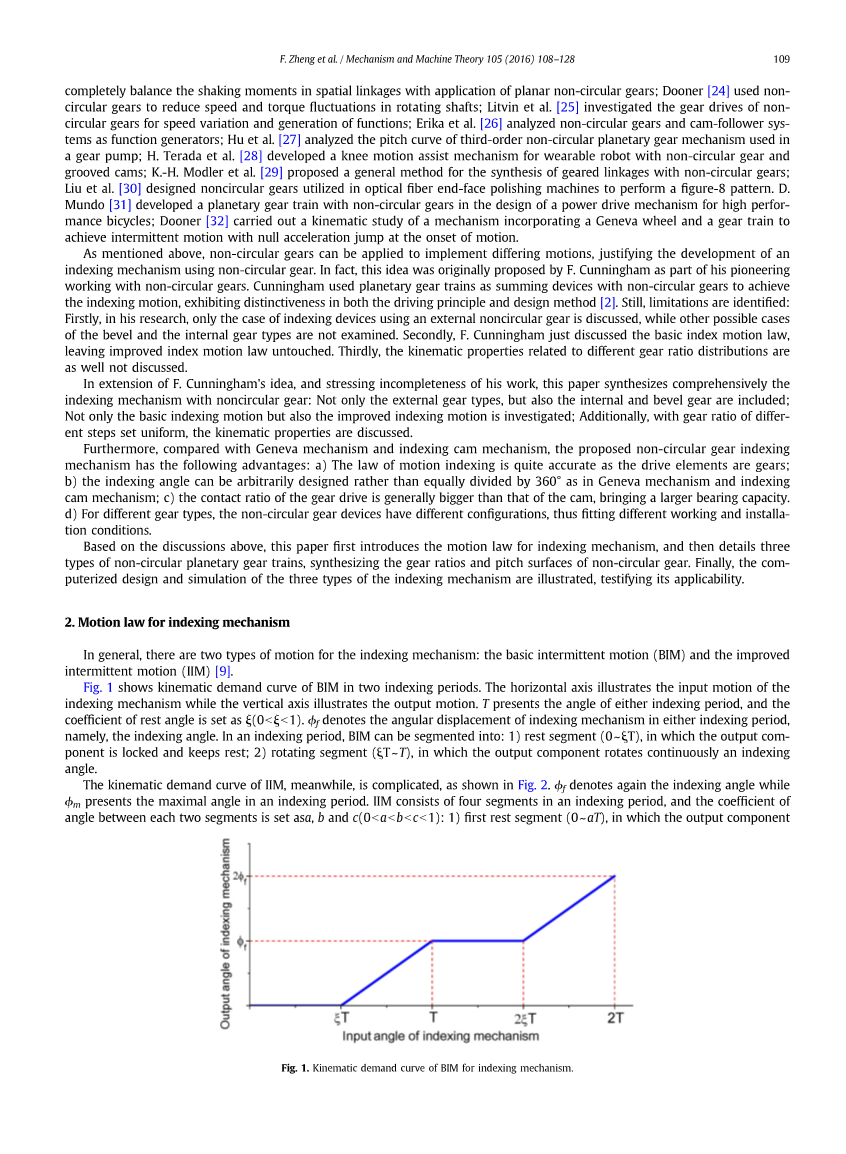
图。 图1显示了BIM在两个分度期间的运动需求曲线。 横轴示出了分度机构的输入运动,而垂直轴示出了输出运动。 T表示任一分度周期的角度,休止角系数设为sect;(0 lt;sect;lt;1)。 ^ f表示分度期间的分度机构的角位移,即分度角。 在分度期间,BIM可以分为:1)休息段(0〜^ T),其中输出组件被锁定并保持; 2)旋转段(^ T〜T),其中输出分量连续旋转分度角。
同时,IIM的运动需求曲线复杂,如图1所示。小f再次表示分度角,而小m表示分度期间的最大角度。 IIM在分度期间由四个段组成,每两段之间的角度系数设为a,b和c(0 lt;a lt;b lt;c lt;1):1)第一休息段(0〜aT)输出组件被锁定并保持静止; 2)旋转段(aT〜bT),其中输出分量连续旋转最大角度lt;^ m; 3)第二休息段(bT〜cT),其中输出分量被锁定并再次保持; 4)后段(cT〜T),其中输出分量在与段2相反的方向上旋转角度 m-^ f。
请注意,BIM是IIM的特例。 (当b = c = 1时)。
代替详细的运动曲线,只有基本运动要求如图1和2所示。然而,实际上,在凸轮机构的设计中,速度的突然变化必须始终被消除,采用几种运动来满足不同的工作条件,例如均匀的加速运动,谐波运动,正弦加速度运动,修正正弦加速运动等[1,2]。
3.非圆形行星齿轮系的系统化
适当的齿轮系的选择形成了使用非圆形齿轮开发分度机构的基础。一般有两种类型的基本齿轮系:普通齿轮系和行星齿轮系。普通的齿轮系应在这里排除,因为它只能用于实现连续旋转。虽然可选择的齿轮系不是唯一的,因为齿轮级数不一致。
经过简要的研究,两步非圆形行星齿轮系被认为是最简单的解决方案。配置不同类型的齿轮,提出三种类型的齿轮系:非圆形外齿轮系(如图3所示),非圆形内齿轮系(如图4所示)和非圆锥齿轮系(如图所示)在图5中)。这些齿轮系的结构不同,使其适用于不同的工作条件。但是,他们仍然具有共同的理论运动学关系,便于他们在单一的数学模型中进行讨论。
如图1如图3,4和5所示,每个两级行星齿轮系共有五个元件:行星架(Element
0),太阳齿轮(元件1),第一行星齿轮(元件2),第二行星轮(元件3)和输出齿轮(元件4))。太阳齿轮1固定在基架上。行星架0沿着基架上的固定旋转轴线旋转并由输入运动驱动。第一行星齿轮2和第二行星齿轮3刚性连接并且在行星架0上共享相同的旋转轴。输出齿轮4提供输出运动。此外,行星架0,太阳齿轮1和输出齿轮4都是同轴的。
2. 齿轮比分布合成
每个元件的角速度分别假定为omega;0,omega;1,omega;2,omega;3和omega;4以及对应的角位移为phi;0
phi;1, phi;2, phi;3和phi;4.对于部分中讨论的齿轮系 3,运动学的基本关系是:
基于运动学反演方法,假设行星架的角速度为零,其他元素的角速度可以如下获得:
齿轮1与齿轮2与传动齿轮角位移功能之间齿轮3与齿轮4之间的传动比满足以下关系:
表一:每种情况的运动方案
信号由齿轮形式决定:当轴角度Sigma;lt;90(外齿轮型)为正时,轴角Sigma;gt; 90(内齿轮型)为负。 因此,使用运动学反转方法,齿轮1和齿轮3的角位移可以被定义为输入角的函数phi;0,即
齿轮系的总传动比可以作为输入角的函数表示:
其中,信号不受等式的信号的影响。 (3)并且保持为正,如术语i12[phi;1(phi;0)]i34[phi;3(phi;0)]保持正(每个齿轮在相同的齿轮系中由相同类型构成)。 因此,为了研究方便,所有齿轮比功能的信号设置为正。
在此基础上,齿轮系的输出角度可以通过整合传动比来获得
考虑到分度输出运动(BIM和IIM)的特征和方程 (6)在齿轮列车设计中必须满足以下两个基本条件:
在休息时间内,输出角度phi;4(phi;0)=0,这个能成立,如果,
在整个分度期间,输出角为phi;4(phi;0)=plusmn;Фf;这意味着,
注意,分度角Фf可以是正的或负的,以呈现相对于输入运动的输出运动的旋转方向。
图6. 正负分度角的齿轮比
考虑到上述条件,为了实现分度运动,必须将至少一个齿轮级设置为非圆形。 显然,将一步的齿轮比分配为不均匀,另一个为均匀,为齿轮系的设计和制造带来了很大的便利。 而本文中并没有探讨另一种分布,其中两个步骤设置为非圆形,复杂且似乎不切实际。
在这方面,将齿轮系的齿轮级设定为非圆形,两齿轮比分布。 结合BIM和IIM两种分度运动,将在下面的齿轮比推导中讨论四种情况,如表1所示。在BIM的推导中,将第一档位设置为圆形的情况称为案例 1,在将第二档齿轮设置为圆形的情况下,情况2.在对IIM的推导中,相应设置下的情况称为情况3和情况4。
-
- BIM的齿轮比
图中BIM的运动需求曲线。 1可以通过以下等式呈现
尤其是,phi;4(T)=Фf
-
-
- 情况1
-
在情况1中,将第一档位的齿轮比设定为参数A1
齿轮1和齿轮3的角度,即公式 (4)可以表示为:
其中信号由齿轮类型决定,如等式(3)。
在这种情况下,齿轮3和齿轮4被设定为齿轮比i#39;34((p3))的共轭非圆形齿轮对,从动齿轮4的角度可以如下计算:
为了满足俯仰面的闭合状态[25],每个齿轮的圆圈必须等于2n,
其中,Tii和Toi是齿轮3和4的对应圆。这意味着如果驱动齿轮3的角度为Tii,则从动齿轮4的角度必须为Toi,即
基于公式 (11),输入齿轮的圈必须为
替代方程 (10),(14)和(15) (6)中,第二基本条件(如式(8)所示)可以表示为
参数A1可以如下求解
根据第一基本条件(如式(7)所示),可以获得齿轮比i34((p3)),当
考虑到连续和可导出的齿轮比函数i#39;34((p3)),该曲线的第一段必须满足公式(17),而第二段(sect;Ti1^(p3 lt;Ti1))可以是满足边界条件 连续和可推导),这里,将sinu?soidal加速度曲线应用于第二段,并且通过假设差分* #39;34(93)如下:
其中,B1是未确定的参数。 而齿轮比i34(93)可以通过等式 (18)在变量93上如下
此外,从动齿轮的角度可以通过公式 (12),参数B1可以按照等式 (14)用数值方法。
请注意,根据方程式 (15),输入角T1 lt;0的周期。 在这个意义上,当^ f lt;0时,分度运动的方向与输入运动的方向相同,而当和gt; 0时,它们彼此相反。 然而,实际上,输出运动的方向没有严格限制,可以通过改变输入运动的方向来反转。
在等式(16)中,设计中输出运动的方向影响参数Ai,进一步影响齿轮比以及非圆形齿轮形状。非圆形齿轮设计的基本思想之一是减小齿轮比功能的范围,这将影响底切,接触比,动态性能甚至制造。基于公式(19)中,齿轮比函数i#39;34((p3))的最小值与最大值之间的绝对差可以求解为| 2B1(1-sect;)|,表示该值由B1决定,此外,在调查齿轮比功能的特点,发现参数B1的值也影响参数A1。
图。图6显示了通过采用相反的分度角信号的齿轮比i#39;34((p3),设计参数设置为和=plusmn;0.314,sect;= 2/3,nn = no1 = 1。和的信号为正红色曲线,蓝色曲线为负,正,负情况参数分别为A1 = 19/20,B1 = -0.4012和A1 = 21/20,B1 = 0.51585,观察曲线,可以绘出两条曲线:当0碎3 lt;sect;Ti1时,红色曲线的值大于蓝色曲线;当Ti碎3 lt;Ti时,红色曲线为凹面,蓝色曲线为凸形;幅度为红色曲线比蓝色曲线小。
在这方面,正分度角被证明是最优的设计(也可以通过调查12B1(1-sect;)|的值在两种情况下得出),即<!--
全文共9723字,剩余内容已隐藏,支付完成后下载完整资料

英语原文共 21 页,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[142879],资料为PDF文档或Word文档,PDF文档可免费转换为Word


