基于变形协调的两级三分支星齿轮传动负荷分配分析外文翻译资料

英语原文共 13 页

基于变形协调的两级三分支星齿轮传动负荷分配分析

杜金福，金茂，刘凯，崔亚辉，赵国睿

摘要：本文针对多分支星齿轮变速器提出了一种负荷分配分析方法，该方法由多个闭环动力流组成。推导出了两级星形齿轮传动的力矩平衡方程和变形相容方程，与行星齿轮传动中使用的方程明显不同。然后建立了负荷分担分析模型，系统研究了两级三分支星形齿轮的负荷分担行为，并对一些未触及的方面进行了研究。结果表明，沿着啮合线方向是太阳和星形齿轮装配误差对负载分配的最敏感的方向。每个分支的太阳齿轮制造误差的大小和方向对负载分配的影响是相同的，太阳或某个星形齿轮制造误差的初始方向对系统的负荷分担系数没有影响，但是装配误差的初始方向会产生影响。并且获得了载荷分布曲线重复第一轨道的条件。最后，采用三分支星形齿轮减速器的数值算例验证了该方法的可行性，计算结果与先前公布的验证模型吻合良好。

关键词：负载分配，星形齿轮传动，多分支，闭环功率流，误差

介绍

众所周知，多分支齿轮传动装置可以通过将输入功率分成多个平行路径而显著减小每个路径的负载，同时提高系统的功率密度比并使结构更紧凑。星形齿轮系是一种固定轴多分支齿轮传动，与行星齿轮变速器相比，在强度，刚性和工作可靠性方面具有明显的优势，使其在航空和汽车工业中得到广泛应用。

然而，只有当负载均匀地分布在所有路径中时，才能实现多分支齿轮传动的这些优点。由于制造和装配误差的存在，这种理想的负载分配不容易获得。为了解决这个问题，业内已经进行了广泛的研究。Hayashi等人、Ma和Botman、Hidaka和Sugimoto专注于行星齿轮传动的负载分配，并讨论了齿轮误差和不对齐对负载分布的影响。Yanabe等人研究了位置偏差和轴承刚度对星形齿轮传动中载荷分担的影响。Sikorsky提出了一种带有两个分支的动力分离式齿轮传动装置，并将其应用于Comanche直升机的主减速器。Krantz和Delgado随后在NASA进行的实验分析静态负载共享行为。Yoshino等人探讨了星形齿轮传动中浮动太阳轮的自定心特性。Kahraman及其同事通过实验和模拟系统地研究了行星齿轮传动的负荷分配特性。Singh及其同事提出了分析模型和行星齿轮负载分担行为的物理解释。Qiu等人通过考虑重力的影响来研究大型风力涡轮机中的行星齿轮的负载分担特性。Iglesias等人对行星定位误差对行星传动的负荷分配的影响进行了系统的研究。Fang等人分析了具有三个分支的星形齿轮系统的动态行为。Bao和Zhu研究了两级星形齿轮传动的静载荷分配特性，并计算了基本分量的偏差。Yuan等人讨论了静态负载分配与基本组件的制造和装配误差之间的关系。

然而，在上述研究中应用的负荷分担分析方法仅考虑了相邻部件之间的机械平衡关系，并且在考虑由多个系统组成的系统时，对多分支齿轮传动的负荷分担行为的研究很少。闭环功率流在相同的闭环功率路径中的所有齿轮之间发生变形兼容性条件由作者确定，在同一闭环动力路径中的所有齿轮之间发生变形兼容性条件，并在先前的研究中进行了展示和验证。为了揭示多分支动力分离式齿轮传动装置的基本特征，不应忽视这一特性。但是这些研究没有区分太阳和行星传动之间在变形兼容性方程方面的差异，但是方程不太严谨，因为在行星齿轮传动中，行星轮与太阳轮和内齿轮啮合，但在两级星形齿轮传动中，太阳轮在第一阶段与行星齿轮啮合，内齿轮在第二阶段与行星齿轮啮合。只有当同一轴上的两个行星齿轮的齿数相等且轴的扭转和弯曲变形被忽略时，行星齿轮传动的推导过程才能用于两级星形齿轮传动。

在此，描述了一种利用变形兼容性对三分支星形齿轮传动进行负荷分担分析的新方法，并进行了严格的推导和验证。还阐明了星形齿轮传动的负载分担行为的一些未涉及的领域，例如同一分支内不同级的负载分担系数之间的关系，以及负载分配中的中心齿轮组件误差的最敏感方向。还详细说明了星形齿轮组件在负载分配上的最敏感方向，并描述了负载分布曲线重复第一轨道的条件。最后，提供了关于这项研究的一些总结性评论。

力矩平衡和变形相容方程

两级三分支星齿轮

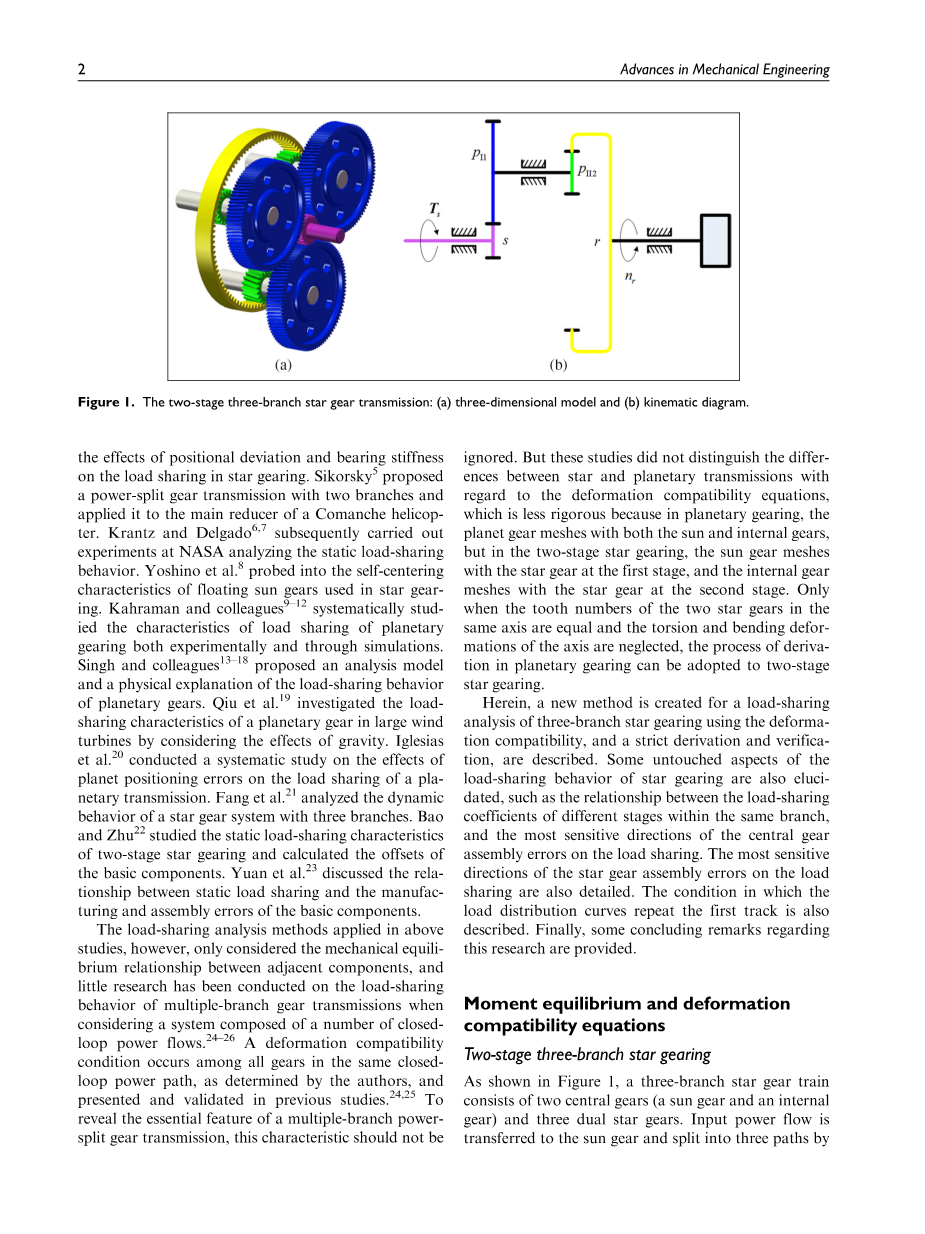
图1所示，三分支星形齿轮系由两个中心齿轮（太阳齿轮和齿圈）和三个双行星齿轮组成。输入功率流被传递到太阳轮并分成三个路径，双星齿轮的第一级（pIi，i=1,2,3）通过第二级（pIIi）经过齿圈，最后通过与齿圈连接的旋转轴输出。这里，I和II分别代表第一和第二阶段。i代表每个阶段的第i个行星档。

为了确保输入扭矩的均匀分布并且不需要额外的负载分配机构，浮动中心齿轮广泛应用于工程中，使整个传动系统紧凑可靠。考虑到联轴器主轴相对粗短并且星形齿轮通常不用作浮动部件，第一和第二星形齿轮之间的联轴器主轴的扭转和弯曲变形以及双行星齿轮的轴承弹性都在此研究中被忽略了。

系统扭矩平衡方程

三分支星形齿轮系的机械模型如图2所示。轮齿可被视为弹性体，并在负载下发生扭转和接触变形。中心齿轮采用弹性支撑。这里，下标s和r分别代表太阳齿轮和内齿轮。Ts表示输入扭矩，s表示太阳齿轮，Tij表示从齿轮j施加到齿轮i的扭矩。每个档位之间的扭矩是TspIi、TpIIir、TpIis、TrpIIi，其中pIi是第一阶段第i个星形齿轮，pIIi是第二阶段第i个星形齿轮。例如，TspIi表示在第一阶段（pIi）从第i个星形齿轮施加到太阳轮的扭矩。假设驱动扭矩为正，则负载扭矩被认为是负的。

根据太阳和双星形齿轮的力矩平衡条件，可以得到下面的方程组，如图2所示

根据力和反作用力平衡条件，获得下式

是阶段I上星形齿轮的基圆半径，是太阳轮的基圆半径。然后，将式（2）代入式（1）

系统的变形协调方程

如图2所示，每个齿轮副的啮合角度方程如下

其中是齿轮i的旋转角度，是齿轮i相对于齿轮j的角位移，它是Tij的函数，。rbpII是第二阶段星齿轮的基圆半径。无论联轴器主轴的扭转变形如何，都可以得到下式

重要的是要注意和可以用行星齿轮变速器中的行星齿轮的旋转角代替。

第k个分支的传输误差可以转换成相对于太阳轮的等效角位移

然后将等式（4）和（5）代入等式（6）

我们可以看到等式（7）明显不同于行星传动的推导。根据等式（7），可以得到下面的等式

基于上述分析，选择并且，可以得到以下三分支星齿轮系的变形协调度方程，即闭环中等效角位移的代数和为零，比如在s-pI1-r-pII2-s和s-pI1-r-pII3-s的闭环中其值为零

负载分担分析模型

变形引起的角度传递误差

齿轮对ij的啮合传动误差由两部分组成，如式（10）所示

其中是由齿轮j和i之间的初始齿隙引起的相对旋转角。另外，表示齿轮j与i接触后的啮合点处的相对旋转角度。由于具有与Tij相同的符号，因此可以通过以下等式来计算

其中Kij是齿轮对ij的啮合刚度，并且在一般计算中可以使用等效刚度，ri是齿轮i的半径。因此，可以获得以下等式组

由误差和浮动引起的角度传输误差

如果制造和装配误差以及基本元件的浮动可以忽略，则;否则，它由两部分组成。

由制造和装配错误引起的角位移。

图3显示了本研究中提到的制造和装配误差，以及包括第一和第二阶段的双星形齿轮的误差。

这里，制造误差主要是指由齿轮加工过程引起的制造偏心和螺距误差，而装配误差主要是指中心和双星齿轮的装配偏心。（E，eta;）表示制造误差，（A，theta;）表示装配误差，其中E和A分别是齿轮的制造和装配偏心的尺寸，而eta;和theta;是制造的位置角和偏心率。另外，phi;i=2pi;（i-1）/3是双星齿轮i的相位角。

由制造和装配误差引起的所有角位移如下

其中下标s，pIi，pIIi和r分别代表太阳轮，第一和第二级上的星形齿轮i和齿圈。另外，alpha;W和alpha;n分别表示外部和内部传动装置的啮合角度;omega;s，omega;p和omega;r是太阳齿轮，星形齿轮和内齿轮的角速度;t表示时间。εw和εn是外部和内部传动装置的基本螺距误差。如上面的等式所示，，，和是随时间变化的函数，而，，，，和是不随时间变化的。假设远离齿面的方向是正的，并且中心齿轮的中心是系统的坐标原点。

然后可以使用等式（14）计算每对齿轮的累积角位移

由基本组件浮动引起的角位移。由基本部件的浮动引起的角位移如下

其中xs，ys和xr，yr是中心齿轮的偏移量，Wi=phi;i pi;/2-alpha;W是第一级上太阳轮和行星齿轮i的啮合线方位角，Ni=phi;i pi;/2 alpha;n是星形齿轮i的啮合线方位角和第二级上的内齿圈。

因此，可以使用等式（16）计算由这种误差和浮动引起的整个角位移。

通过将等式（11）和（16）代入等式（10），可以如下获得角度传输误差

中心齿轮的轴承刚度和浮动

太阳齿轮和内齿轮的轴承刚度和浮动如下

其中Ks和Kr代表太阳轮和内齿轮的轴承刚度。

系统的负载分担系数

等式（3），（9），（17）和（18）的解是TspIi，TpIIir和xs，ys，xr，yr。每个分支和阶段的负载分担系数可以通过等式（19）和（20）计算

其中，Ts/3且rbpI/rbs（Ts/3）分别代表齿轮对spIi和pIIir的理想输入转矩。由双行星齿轮的力矩平衡条件得

因此

然后将系统的负载分担系数定义为G，并且可以使用式（23）计算

数值例子和讨论

基于上述分析，计算了航空中使用的两级三分支星齿轮减速器的载荷分布。该减速机齿轮的基本参数如表1所示。转速为20000r/min时输入功率为1250kW。第一和第二级的等效啮合刚度为1*106N/mm。太阳和内齿圈的轴承刚度为9.42*103N/mm。应该注意的是，第一级和第二级上的两个星形齿轮的螺旋通常设计成相同的，以减小双星齿轮轴上的轴向力。然而，由于每级上的不同负载和结构要求，第一级和第二级上的两个星形齿轮的螺旋角大小不一定相等。

制造和装配错误对负载分配的影响

误差敏感性分析资料编号：[4898]

您可能感兴趣的文章

• 噪音和振动测量外文翻译资料
• 主动式横向稳定杆在车辆平顺性和稳定性上的应用外文翻译资料
• 干摩擦离合器系统的应力与变形分析外文翻译资料
• 电动转向模拟器的虚拟样机外文翻译资料
• 主动前转向系统控制策略研究外文翻译资料
• 横向冲击对汽车乘客颈椎反应的三维分析.外文翻译资料
• 对机车意外事故中新型胸腔安全系统的评估外文翻译资料
• 电动车动力传动系统性能分析解析算法的发展外文翻译资料
• 扁钢表面缺陷的自动检测:综述外文翻译资料
• 非线性规划二:无约束优化技术外文翻译资料