
英语原文共 15 页,剩余内容已隐藏,支付完成后下载完整资料
自动驾驶车辆系统的预测主动转向控制
摘要:在这篇文章里提出了一种基于模型预测控制(MPC)理论的主动前轮转向的自动汽车控制方法。假设在限定的水平面上汽车的轨迹在每一个时间步长里是已知的,然后一个MPC控制器输出一个前轮转角使得汽车以尽可能快的速度在湿滑的路面上追踪规划好的路径。我们提出了两种不同计算复杂性的控制方法。第一种方法是建立在非线性汽车模型上运用MPC理论。第二种方法则使用连续在线线性汽车模型。文中讨论了两种控制方法的计算复杂度及性能。通过仿真及实验,证实提出的基于MPC理论控制的汽车最高可以以21m/s的速度在冰雪路面上行驶。
关键词:主动转向;自动驾驶车辆;模型预测控制;非线性优化;车辆动态控制;车辆稳定性
Ⅰ.引言
汽车行业近些年的发展趋于增加电子产品、计算机以及主要改善整个系统的性能和鲁棒性的控制器。这种趋势影响着整个汽车行业,特别是在主动安全领域,因为主动安全有效的弥补了被动安全的劣势。被动安全着重于保证车辆的结构完整性,而主动安全恰恰相反,主动安全主要用于避免事故并同时改善车辆在紧急情况下的操纵和稳定性,特别是在突然遇到路滑的道路[10]。
开始研究主动安全系统的时间需要追溯到1980年,早期的研究主要着重提高汽车的纵向动力学部分,特别是在更有效的制动系统(ABS)和牵引力控制系统(TC)。ABS系统通过避免车轮抱死打滑来提高制动效率。TC系统防止车轮打滑,同时通过最大化车辆轮胎和道路之间的牵引力和侧向力来提高车辆的稳定性和转向性。接下来是针对不同的车辆稳定性控制系统[34](这些熟知的各种稳定系统的缩写如电子稳定程序(ESP),车辆稳定性控制(VSC),交互式车辆动力学(IVD)和动态稳定性控制(DSC))基本上,这些系统通过控制一侧的制动和发动机扭矩来控制车辆的横摆运动从而达到稳定在极限情况下行驶的车辆的目的。
除了制动和牵引系统之外,主动转向系统(AFS)还利用前轮转向指令来改善侧向车辆的稳定性[1-2]。此外,转向指令可用于抑制不同附着系数路面上的行驶阻力,不对称制动力,或风[21]。四轮转向(4WS)系统遵循类似的目标。例如,在文献[3]中,Ackermann等人提出了四轮转向装置中的路径跟随和外部干扰排斥之间的解耦策略。自动汽车转向系统被分成跟随路径和偏航稳定任务,第一个是通过前转向角实现的,后转向角通过后转向角实现。
主动前轮转向系统的研究也从自动驾驶车辆的角度出发。在文献[16]中,提出了一种用于高速公路自动化的自动转向控制系统,其中车辆配备有磁性传感器放置在前部和后部保险杠上,以检测用电线[13]和磁性标记[36]实现的车道参照。最近的例子是AFS在自动驾驶汽车中的应用是“大挑战”赛车的驾驶[5],[23],[30]。
在本文中,预计未来的系统将能够提高主动安全干预的有效性,将高于目前可干预有效性的范围。这不仅可以通过附加的执行器类型(例如4WS,主动转向,主动悬架或主动差速器)来实现,而且还可以通过附加的传感器信息(例如车载摄像头)以及红外和其他传感器替代品来实现。所有这些将会更进一步辅以全球定位系统(GPS)信息包括预先存储的映射。在这种情况下,有可能想象未来的车辆将能够识别障碍物在路上,如动物,岩石或倒下的树木/树枝,以及按照最佳路径协助司机避开障碍物,同时保持车辆通行与进入的交通安全距离的道路。另外的信息来源也可以来自周围的车辆和环境,这些车辆和环境信息可以从前方车辆检测并传递过来路况的信息获得,这可以向控制器提供大量的预览。如果车在冰雪覆盖的表面上行驶时这样的信息是很有用的。因为在这种情况下,很容易达到车辆处理能力的极限。
预测传感器和基础设施能提高信息和控制执行机构的集成度,现在的疑问是在给定的避障情况下控制车辆操纵的最佳方式是什么。
我们假设一个轨迹规划系统是可用的,并且我们考虑在湿滑路面的双车道上变道的场景,车辆配备有完全自主的导航系统。在本文中,我们将重点放在通过主动转向控制偏航和侧向车辆动力学。控制输入是前转向角,目标是尽可能接近期望的轨迹或目标,同时满足反映车辆物理限制和设计要求的各种约束。未来期望的轨迹仅在每个时间步长的有限时间范围内是已知的。这是根据模型预测控制(MPC)[14],[26]理论完成的,与我们2000年初正在进行的内部研究工作(参见文献[7]和其中的参考文献)一致。
在本文中,AFS MPC有两种不同的控制理论将被提出并进行比较。第一个遵循文献[7]中提出的工作,并使用非线性车辆模型来预测系统的未来演变[26]。由此产生的MPC控制器需要在每个时间步骤解决非线性优化问题。我们将证明,计算负担目前是高车速下实验验证的障碍。第二个控制理论试图克服这个问题,并基于非线性车辆模型的连续在线线性化提出了次优的MPC控制器。这是在每个时间步的当前工作点周围线性化的,并且线性MPC控制器被设计用于所产生的线性时变(LTV)系统。使用时间变化模型的想法可以追溯到20世纪70年代早期的过程控制领域,尽管它仅在最近才被恰当地形式化。在文献[9],[18],[20],[22]和[35]中可以找到研究在线参数变化(LPV)MPC方案。其中,文献[18]和[20]中的工作与我们的方法最为接近,它为预定的LTV模型提供了MPC方案,该方案已在波音飞机上成功验证。一般来说,这种方案的性能高度依赖于模型的非线性。事实上,当状态和输入轨迹偏离当前操作点时,模型失配增加。这会产生很大的预测误差,从而导致闭环系统的不稳定性。我们将证明,在我们的应用程序中,可以引入状态约束来显着提高系统的性能。实验结果表明,在冰雪路面上,车辆可以稳定在21米/秒。最后,介绍一种具有一步控制时域的LTV MPC。这可以调整以提供可接受的性能,并且不需要任何复杂的优化软件。
我们实时在客车上安装了MPC控制器,并对积雪路面和冰雪路面进行了测试。本文的最后部分描述了实验装置,并给出了所提出的MPC控制器的实验和仿真结果。值得注意的是,我们在文献[7]中的早期工作只关注车辆动力学模型和非线性MPC方案的仿真结果。此篇文章的结构如下。第二部分介绍所使用的汽车动力学模型并简要讨论了一下轮胎模型。第三部分介绍了一个简化的自动驾驶车辆指导分层框架。本文的贡献和研究课题将在现有的工作和未来的研究中进行详细的阐述。第四节阐述了使用非线性和线性预测模型时的控制问题。第V节描述了双车道变更情景,而第VI节则介绍了实验和仿真结果。接下来是第七部分的结束语,其中强调了未来的研究方向。
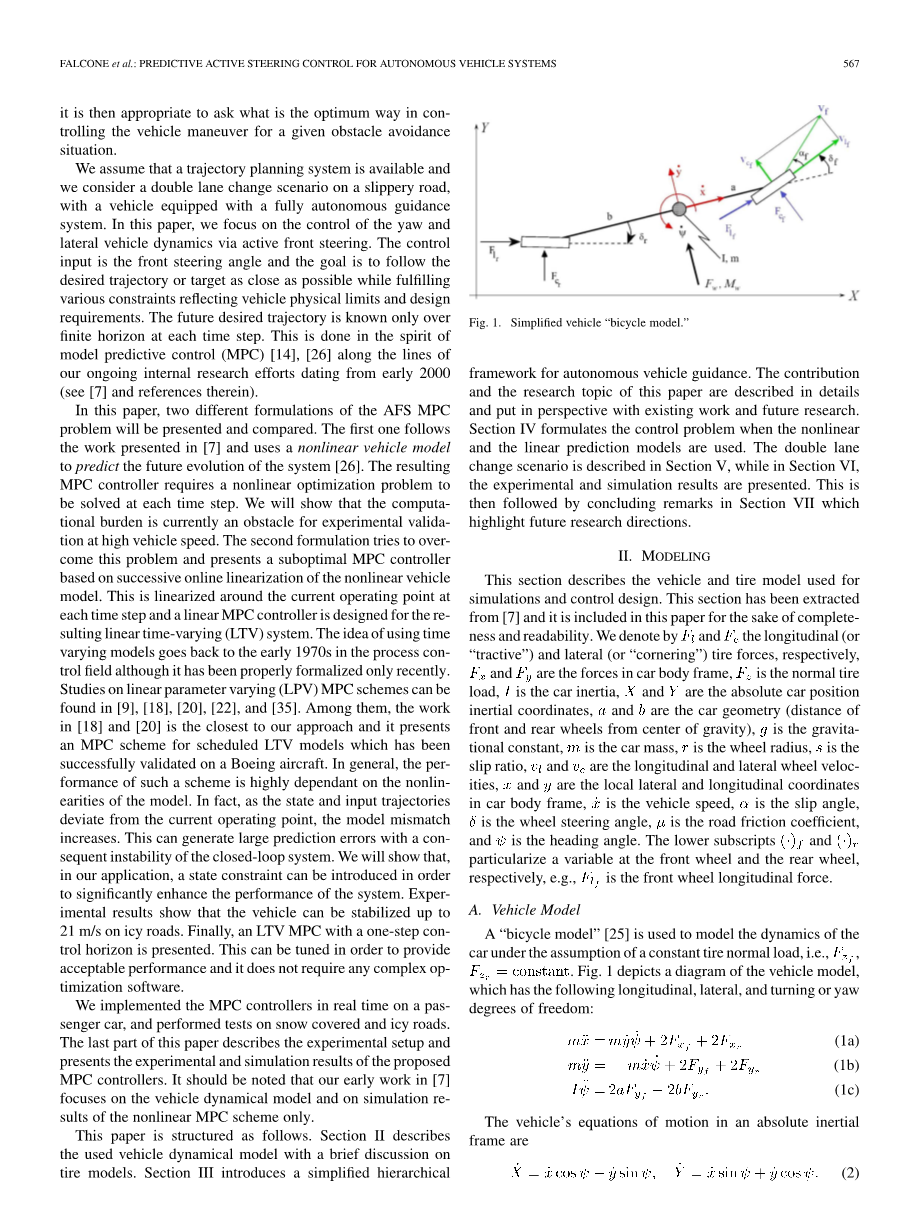
图1.简化车辆“自行车模型”
II.模型
本节介绍用于仿真和控制设计的车辆和轮胎模型。本节已经从[7]中提取出来,为了提高本文的完整性和可读性,它被包含在本文中。我们使用Fl和Fc分别表示轮胎的纵向(或“牵引”)和侧向(或“转弯”)轮胎力,此外,FX和FY是车身车架所受的力,Fz是轮胎正常载荷,I表示汽车惯性,X和Y是绝对的汽车位置惯性坐标,a和b是汽车的几何形状参数(表示前后轴距离重心的纵向距离),g是重力常数,m是汽车质量,r是车轮半径,s是滑移率,ul和uc是纵向和横向车轮速度,x和y是车身框架中的局部横向和纵向坐标,是车速,alpha;是滑移角,delta;是车轮转向角,mu;是路面摩擦系数,psi;是方位角。下脚标(.)f和(.)r分别在前轮和后轮处分别具有的变量,例如Flf前轮纵向力。
A.车辆模型
一个“自行车模型”[25]被用来模拟在恒定的轮胎正常负荷的假设下汽车的动力学,即在Fzf,Fzr为常量情况下,图1描绘了车辆模型的图,其具有以下纵向,横向和转向或偏转自由度:
在绝对惯性中车辆的运动方程为:
车轮的运动方程描述了横向(或转弯)和纵向车轮速度:
其中delta;f和delta;r分别是前后轮转向角度,以及:
下面前后轴受力方程中会使用相应的下标来表达所有变量,纵向和横向的轮胎力量导致下列力作用于重心:
每个轮胎的受力有下面方程确定:
alpha;,s,mu;和Fz这几个参数接下来会定义。轮胎滑移角alpha;表示车轮速度矢量与车轮自身的方向之间的角度,并可以紧凑地表示为:
滑移率定义如下:
其中r和w分别是车轮的半径和角速度,参数mu;表示道路摩擦系数,假定前后轮相等。Fz是车辆的总垂直载荷,并且基于汽车模型的几何结构分布在前轮和后轮之间(由参数a,b描述)
式(1)-(9)中描述的非线性车辆动力学可以用下面式子的改写:
其中明确突出了每个时刻对滑动率s和摩擦系数值mu;的依赖性。状态和输入向量分别为和u=delta;f。在本文中,假设在任何时刻delta;r都为零。
模型(10)表示了与车辆横向稳定性相关的最相关的非线性。第二节简要介绍轮胎力Fl和Fc和模型。
图2.轮胎纵向力和侧向力与道路附着系数
B.轮胎模型
除了空气动力和重力外,影响车辆操纵的所有力都由轮胎产生。轮胎力提供主要的外部影响,并且由于其高度非线性行为,导致整个纵向和横向车辆操纵性能的最大变化侧向机动范围。因此,使用真实的非线性轮胎模型非常重要,特别是在研究导致响应接近车辆操纵能力极限的大型控制输入时。在这种情况下,车轮的横向和纵向运动通过轮胎力强耦合,并且滑动比和滑移角可能同时出现较大值。
大多数现有轮胎模型主要是“半经验”的实体。也就是说,轮胎模型结构是通过分析考虑确定的,关键参数取决于轮胎数据测量。这些模型的范围从极其简单(其中横向力计算为基于一个测量斜率当alpha;=0和一个测量值为最大横向力的函数)到相对复杂的算法,其使用在许多不同负载和滑移角处测量的轮胎数据。
在本文中,我们使用Pacejka轮胎模型[4]来描述(6)中的轮胎纵向和转弯力。这是一个复杂的半经验非线性模型,它考虑了纵向力与转向力联合制动和转向时的转向力之间的相互作用。假设纵向力和转弯力取决于法向力,滑移角,表面摩擦系数和纵向滑移。图2描述了纵向和横向力对纵向滑动和滑移角,对于摩擦系数的固定值。我们称“自行车”模型的前轮代表实际车辆的两个前轮胎。
图3.用于完全自主车辆引导系统的简化架构
Ⅲ.自动驾驶汽车指导的分级框架
在本节中,我们借用图3中来自航空航天领域的简化示意架构[8][24][31],以解释我们的方法和贡献。图3中的架构描述了 自主车辆引导系统,它由四个模块组成:轨迹/模式发生器,轨迹/模式重新规划,低级控制系统,车辆和环境模型。轨迹/模式计划模块预先计算车辆轨迹以及操作模式更改的时间和条件。在航空航天领域,操作模式选择的例子包括:在壳牌汽车领域,可以包括两种或更多种能源(即气体,电力,氢气)或(在一个非常未来的情况下)在不同的车辆形状之间变形。
可以在轨迹/模式重新规划模块的驱动期间基于当前测量结果,固定点或某些事件的发生(例如超过特定界限的跟踪误差,硬件故障等)来在线重新计算流线的轨迹和操作模式。过度的风,弹出障碍的存在)。
基于来自轨迹/模式重新计算的传感器测量,状态和参数估计和参考命令,低级别控制系统命令诸如前后转向角,四个制动器,发动机扭矩,有源差速器和主动悬架的车辆致动器模块。这种参考命令可以包括横向和纵向位置,俯仰,偏航和滚转速率。低层控制系统的目标是使车辆尽可能接近当前计划的轨迹但是并未考虑到测量噪声、不完整的动力学模型、参数不确定性以及尚未(或尚未)考虑到的车辆和道路状况的突然变化等因素的影响。特别是,当车辆运行在其稳定极限附近时,必须考虑这些额外的噪音,干扰和不确定性,可能通过检测车辆的内部状态并进行补偿。例如,如果后轮胎饱和,一个熟练的驾驶员会将他/她的转向输入从通常的转向命令切换到用于稳定车辆的反向转向命令。可以想象的是,如果指挥转向只是期望轨迹和车辆当前位置和航向的函数(不考虑附加车辆动态状态)自动转向不会产生必要的稳定输出。
我们注意到图3中的方案是一个过度简化的方案,并且在轨迹/模式重新规划模块和低级控制系统模块中都可能存在额外的层级。前三个模块的结合通常被称为导航和导航控制(GNC)系统。
通常,轨迹重新规划者和低级控制系统模块不共享关于环境和车辆的相同信息。例如,重新规划算法可以使用来自摄像机或雷达的信息,这些信息可能不在较低的层面上使用。而且,典型地,轨迹重新规划模块执行的频率低于下级控制系统的频率。两个模块的设计都使用了具有不同细节层次的车辆和环境模型。用于设计这两个模块的动力学模型的脆弱性在许多因素中由性能/计算资源折衷决定,并且在文献中没有公认的标准。这两个模块的可能控制范例之一在于使用高保真车辆模型来设计较低级别的控制器,而轨迹规划器依赖于较粗糙/较不详细的车辆动力学模型。显然,在较高级别上使用的模型的硬度越高,较低级别控制算法的工作就越容易。
关于GNC算法的研究在:(1)焦点(轨迹重新规划者和/或低层控制系统)有所不同;(2)使用的车辆动力学模型的类型;(3)使用的控制设计的类型;(4)输入和传感器选择。
在文献[23]中,轨迹重新规划模块基于时间
全文共7393字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[15787],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


