英语原文共 11 页,剩余内容已隐藏,支付完成后下载完整资料
双皮带传动中平带偏斜现象的分析
平带传送中一般会出现偏斜现象,即带在运行中沿着滑轮轴向移动。偏斜现象通常是由滑轮安装角度偏差造成的。通常角度偏差可分为两种类型,平面内偏差和平面外偏差。前者驱动轮和被驱动轮的轴线处于同一平面内但不平行,后者两轴线不在同一平面内。在本文中,主要解决由平面外和平面内错位引起的皮带偏斜问题。通过有限元方法模拟提供的理论分析发现:(1)在面外失准的情况下,偏斜率(一个描述偏斜程度的指数)可由一个非常简单的公式确定,其中只需要三个几何参数;(2)在面内失准情况下,偏斜比面外失准情况复杂得多,偏斜率由非线性联立方程组确定,求解非线性联立方程组用迭代方法。两种情况都用有限元分析影响偏斜的因素和结果。
关键词:平带传动,薄膜带,偏斜,横向移动,滑轮不对中,摩擦,理论解,有限元
1.简介
扁平带已被广泛用于工业设备以及家用电器的基本元件中。在自动取款机,火车站自动检票机,自动邮件分拣机(或多线光学字符阅读器)和自动读卡器等机器中我们常常可以看到它们的身影。在这些自动机器设备中,平带通常用于运输纸币,票据和信封或明信片等所谓的小巧的物体。作为平带的一种,薄膜带被用于彩色打印机和复印机中传送纸张或传送图像。
平带传动过程中存在偏斜或横移等问题,是带在运行中沿着滑轮的轴向移动所造成的。偏斜会导致机器停止运行并损坏皮带甚至设备,在打印机和复印机中,带的偏斜会导致纸张排版错位,甚至卡纸。
带的偏斜主要是由滑轮的安装角度偏差造成的。角度偏差可分为两种类型,面内偏差和外面偏差。前者驱动轮和被驱动轮的轴线处于同一平面但不平行,后者两轴线不在同一平面内。一般我们用凸滑轮保持皮带在中心运行,然而,凸滑轮会导致皮带张力集中,从而缩短皮带的使用寿命。此外,凸滑轮很难用于带宽较大的打印机的带式输送系统和薄膜带系统中。
虽然皮带偏斜问题已经存在很长一段时间,但其机制还是没有完全弄清楚,尚且没有很好的理论解决方案。Gerbert 从理论上分析了锥形皮带轮上皮带的横向运动,但没有得到简易的解决方法。Yanabe等人通过实验并采用有限元法(FEM)研究了直滑轮上的带偏斜,他们的研究包括了面内错位和面外错位这两种情况,并得出了在两种情况下滑轮上的斜率比(一个描述倾斜程度的指数)等于皮带的超前角这一结论。工程师为了防止或减少输送系统和印刷机带偏斜而开发了许多方法,例如参考文献中所示。
同时学者还研究了带纵向的力学和滑动特性。例如,Gerbert提出了皮带和V形带的统一滑移理论,Kong和Parker研究了带有滑轮槽皮带传动的力学性质和滑动摩擦,Alciatore和Traver讨论了两个皮带力学理论适用于多路皮带传动的问题。参考文献中还有关于螺旋同步带传动中的侧轨和传动误差的表述。
本文通过有限元模拟的方法讨论了双皮带轮传动的平带偏斜,并推导出偏斜的理论解。在第二部分中,解决了由平面外未对准引起的皮带偏斜。 在有限元分析中,使用基于复印机和彩色打印机中胶片带的驱动,根据有限元模拟结果的讨论推导出确定带偏斜比的数学公式。该公式非常简洁,仅涉及皮带和皮带轮的三个几何参数:皮带长度,偏斜角和皮带轮直径。
在第三节中讨论由滑轮的面内错位引起的偏斜。发现由于皮带的弯曲变形和皮带轮的面内错位引起的皮带偏斜,比由皮带轮的面外错位引起的皮带偏斜要复杂的多。Euler-Bernoulli的梁弯曲理论用于本文的分析,推导了一个确定偏斜率的非线性联立方程组,并提出求解非线性联立方程组的迭代方法。最后,对理论分析与有限元结果进行了验证,并讨论了影响偏斜的因素。
2.平面偏差造成的偏斜
2.1有限元模型与分析方法
长度皮带 L = 730毫米
皮带的宽度 W = 160毫米
皮带的厚度 t = 0.1毫米
皮带的杨氏模量 E = 2.7GPa
滑轮直径 D = 33.6毫米
平面外失准角度 =0.066ordm;
皮带和皮带轮之间的摩擦系数=0.2
滑轮之间的安装张力 F=200N
表 1
表1显示双滑轮胶片传动系统的有限元模型,其中两个滑轮具有相同的直径。O-xyz是全局坐标系,O-xz平面是两个滑轮展开的基准平面。从动皮带轮的轴线位于基准平面内并与z轴平行, 驱动滑轮的轴线平行于平面O-yz,与平面O-xz夹角为,皮带最初沿轴向安装在皮带轮的中心。在这项研究中,假设没有扭矩载荷,并且因为应用了准静态解决方案,所以没有指定旋转速度。
薄膜带采用4节点壳体元件建模,滑轮采用刚性表面建模,接触器接口界定在皮带和皮带轮之间。假定带和滑轮之间具有恒定摩擦系数的库仑摩擦力。本研究中使用的FEM的求解器是ABAQUS/standard。
表1中列出了计算中使用的皮带和滑轮的尺寸和参数。这些数据与用于真彩色打印机的薄膜传送带系统相对应。 在有限元模型中,皮带分为400个周长节点和12个宽度方向节点。FEM仿真步骤如下:(1)沿x方向移动滑轮,直至在安全带上施加所需的安装力,(2)旋转驱动滑轮。观察皮带旋转的三个方面:(1)皮带沿轴向的运动;(2)整个皮带的形状;(3)皮带上的参考点的移动。
可以忽略带在宽度方向上的变形,
因此可以选择带上沿圆周方向的任意线来代表整条带,以观察其运动和形状。 选择位于带中心的节点组成的中心线,中心线上的任意点P选作固定在皮带上的参考点。
为了测量偏斜,如图1所示选择两个间隔固定的参考点a和b。测量a和b的z方向的位移为偏斜量。为了表示偏斜的大小,将无量纲指数定义为 Sr=(1)
其中Sz是带沿轴向移动的距离,即偏斜,St是带纵向的行进距离。Sr象征着偏斜比例。
图 1
2.2仿真结果和现象
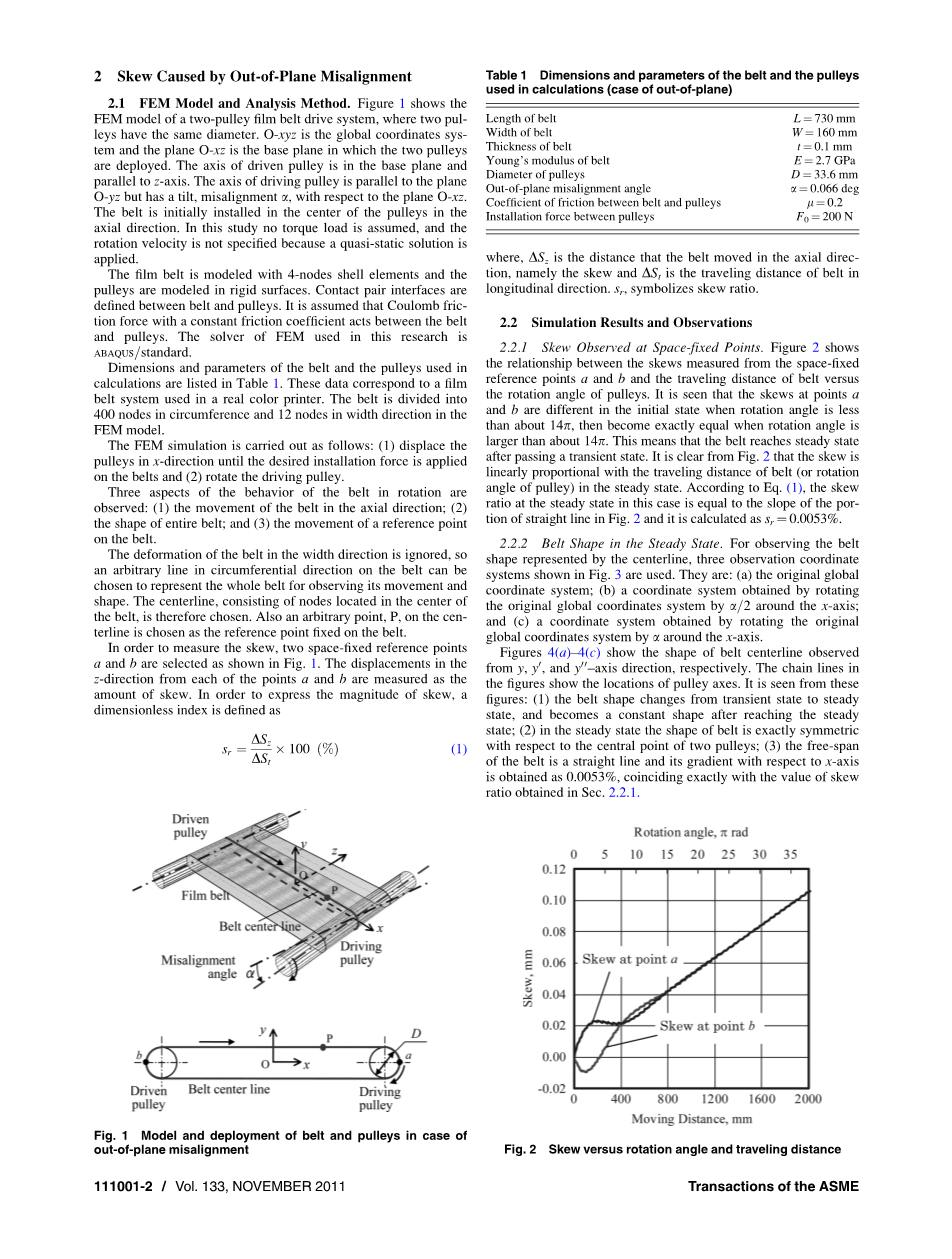
2.2.1 在空间固定点观察偏斜。图2 表示了从空间固定的参考点a和b测得的偏斜,与皮带的行进距离和皮带轮的转角之间的关系。可以看出,当旋转角度小于大约14时,初始状态下点a和b处的偏斜不同,当旋转角度大于大约14时,偏斜变得完全相等。这意味着皮带在经过瞬态后达到稳定状态。从图中清楚可见,偏斜与稳定状态下皮带的行进距离(或皮带轮的旋转角度)成线性
比例。 根据公式(1),在稳定状态下的偏斜率等于图1中直线部分的斜率,Sr = 0.0053%。
图 2
2.2.2稳定状态下的带状。为了观察由中心线表示的带形状,图3中用了三个观察坐标系。它们是:(a)原始的全球坐标系; (b)通过围绕x轴将原始全局坐标系旋转a=2而获得的坐标系;(c)通过围绕x轴旋转原始全局坐标系获得的坐标系。图4(a)–4(c)显示带中心线的形状从y,yrsquo;和yrsquo;rsquo;轴方向分别计算。图中的点划线
表示滑轮轴的位置。从这些图中可以看出:(1)皮带从过渡状态变为稳定状态,并在达到稳定状态后变为恒定形状; (2)在稳定状态下,皮带的形状相对于两个皮带轮的中心点完全对称;(3)皮带的自由跨度为直线,其相对于x轴的梯度为0.0053%,与在第二部分中获得的偏斜比的值恰好一致。
图 3
图5(a)和5(b)显示了驱动和从动皮带轮上皮带中心线缠绕的扩展部分。图中的点表示中心线的节点,实线表示线性近似。很显然,皮带轮上皮带缠绕部分的扩大部分在驱动和从动皮带轮上成直线形状。直线的梯度作为偏斜比值,为0.0053%。
图 4
(a) 图 5 (b)
2.2.3带上参考点的运动轨迹。图6(a)–6(c)表示从y,yrsquo;和yrsquo;rsquo;轴方向分别观察到的参考点P的运动轨迹,与4(a)–4(c)相同 从图6(a)中可以看出,点P似乎在驱动滑轮上沿z方向移动,但不在从动滑轮上或自由跨距上移动。由于从动皮带轮的轴线与图中的z坐标一致,我们可以得出结论,观察点P不会在从动皮带轮上沿轴向滑动。相反,从图6(c)中可以看出, 点P在从动滑轮上沿z方向移动,但不在驱动滑轮或自由跨距上移动。明显可以知道,点P在驱动或从动滑轮上都不会沿轴向滑动。观察到的点P在z或zrsquo;方向上移动的原因如图3和图4所示。6(a) 和6(c) 是由于驱动皮带轮6(a)或从动皮带轮6(c)相对于基准面倾斜一个角度。类似地,6(b)显示点P在zrsquo;方向上在驱动和从动滑轮上移动,但在从yrsquo;轴方向观察时不在自由跨度上移动。两个皮带轮上的移动距离是图6(a) 和6(c)的一半。此外,发现皮带轮上的点P在轴向上的移动距离除以皮带的长度的大小等于在第二节中获得的斜率即0.0053%。
2.3倾斜机制与理论解决方案
2.3.1倾斜的机制。根据第二节中的讨论和意见。在yrsquo;轴方向观察到的稳定状态下带中心线的形状和行为如图7所示。图7(a) 显示了滑轮和整个中心线的形状;图7(b)显示了滑轮上中心线缠绕的扩展形状; 图7(c) 显示中心线的自由跨度。我们不妨看看滑轮上中心线, 假定皮带中心线在特定时间以ABCD状态
图 6
缠绕在皮带轮上,如图7(a)。当皮带轮沿图7所示的方向转动半圈时,7(a)驱动皮带轮上的A点沿平行于基线QR(垂直于皮带轮轴线的圆周)的方向移动到B1,驱动皮带轮AB上的皮带卷绕部分变为A1B1。 由于皮带不在皮带轮上沿轴向滑动,因此A1B1与AB平行。同样,从动皮带轮CD上的皮带缠绕部分变为C1D1。最终整个中心线从ABCD移动到A1B1C1D1。 皮带轮中心线在zrsquo;轴方向上移动的半周期间的距离为
(2)
其中是皮带中心线和皮带轮基线之间的角度,它被称为超前角或螺旋角。带在皮带轮转半圈过程中行进的距离为D= 2。偏斜率可简单推导为
Sr= (3)
可得知偏斜率等于皮带的导角。图8显示了整个带中心线沿着带行进的方向扩展,可以看出3D曲线形状的带中心线在膨胀后变成直线,该直线相对于xrsquo;轴的斜率恰好等于偏斜比。如果皮带轮沿与图7(a)所示方向相反的方向转动半圈,从A1B1C1D1起,整个中心线很快会回到ABCD。这意味着由平面外引起的皮带偏斜的方向取决于旋转方向,或者由于平面外未偏斜而引起的带偏斜随着旋转方向的改变是可逆的。
2.3.2偏斜的理论解决方案
从带中心线的梯度推导,正如在第二节中讨论的,偏斜率等于展开的带中心线的斜率,在这里我们将计算这个斜率。为了方便起见,我们将坐标系O-xrsquo;yrsquo;zrsquo;的原点放在ABCD状态下带中心线的对称中心,如图7所示。坐标系Oxrsquo;yrsquo;z中的点A和D的坐标是
A=(, )
D=(,)
l是驱动和驱动脉冲中心之间的距离, 带中心线的梯度可以从自由跨度AD计算得出:
联立方程(2)和(5)导出:
(6)
根据公式(3),偏差比率推导为:
Sr= (7)
第2节中的示例的偏斜比率可以通过使用公式(7)得到。结果为Sr = 0.0053%,与有限元计算结果完全一致。从皮带上点的运动中推导出来, 如图7(c)所示,自由跨度中的观察点P仅在x0轴方向上移动,而不在z0轴方向上移动。 图9是点P的运动轨迹。当皮带行进一圈时,点P沿轴向移动的距离是:
H=2 (8)
由于运动一圈的距离等于皮带的长度L,所以偏斜率可以推导为:
Sr= (9)
图 7
这与方程式完全(7)相同。方程(7)已经通过Yanabe0s研究提供的有限元计算结果进行了验证,其中D = 76mm和L = 780mm,带偏斜比与失调角成正比:Sr=1.72。公式的结果 (7)是Sr = 1.70,两个结果之间的差异小于1.2%。
- 平面错位造成的倾斜
3.1有限元模型与分析方法。 图10表示具有平面内角度不对准的双皮带传动系统的有限元模型。系统中的两个滑轮具有相同的直径。O-xyz表示全局坐标系,O-xz是由滑轮的两个轴形成的基准平面。 驱动皮带轮的轴线相对于底座平面中从动皮带轮设定偏角。皮带在初始状态下部署在滑轮的中心。
表
全文共10831字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[13847],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。