
英语原文共 8 页,剩余内容已隐藏,支付完成后下载完整资料
旋转机械临界速度和模式的实践回顾
Erik Swanson,北卡罗来纳州Chapel Hill的Xdot咨询公司
Chris D. Powell,俄亥俄州Zoar的结构技术公司
Sorin Weissman, Alfa Wasserman, Inc., West Caldwell, New Jersey
这篇文章的目的是为了展示一个对术语和行为的实际理解,它是基于对轴振动的可视化,以及研究影响振动的问题。希望这个演示能帮助非专业人员更好地了解机器上正在发生的事情,并且专家可能会获得不同的观点和/或一些新的例子。
对于不熟悉旋转机械振动的一些独特特性的工程师来说,机器的术语和行为似乎是压倒一切的。像大多数专业领域一样,有许多优秀的文章,但是很难快速地提取出需要的实用的见解。在另一方面,也有大量的集中于识别问题和特征的故障诊断资源,但只提供有限的见解。最近综合实验和分析工作的讨论提出了一篇文章的可能性,这篇文章试图从一个不太重要的角度更深入地了解旋转机械振动的一些基本特征。
因此,我们开始着手讨论几个对理解旋转机械振动很基本的问题:
1. 什么是“临界速度”?
2. 临界速度是如何与共振和固有频率相关联?
3. 轴转速变化时固有频率如何变化?
4. 轴转动固有频率与结构中更常见的固有频率和模态有什么不同?
5. 轴承特性有什么影响?
振动直觉
作为探索世界的孩子的一部分,每个人都熟悉这样一个想法,即在结构上敲打会使其反弹并振动。 有些物品比其他物品更容易振动(例如金属杆与木棍)。我们也有这样的直觉:在特定的频率下,让物体振动或前后移动更容易。 例如,我们倾向于认为,用长绳前后摆动比用短绳摆动慢得多。以与秋千前后自然摆动速度相匹配的速度“摆动”秋千,这将使你的摆动幅度远远高于比秋千固有频率快或慢的频率。
我们中的许多人也有一些弦乐器的使用经验。 根据这种经验,我们发展出一些想法,即重物(粗弦)倾向于以比轻物体(细弦)更低的频率振动。 我们知道增加刚度(收紧琴弦)会提高其振动的频率。 最后,我们还知道,小主要尺寸(较短的弦)会导致较高的频率振动。
结构振动简要回顾
作为工程师,我们知道振动特性是由结构的质量和刚度值决定的,而阻尼(消散振动能的能力)通过控制振幅发挥不可或缺的作用。 这种教育通常从最简单的系统开始 -它是一个连接在弹簧上的刚体,如图1所示。
图1.简单弹簧-质量系统
用这个简单的系统,我们量化我们对振动频率的直觉(较重的物体导致低频,更硬的弹簧产生更高的频率)。经过一番努力,我们得出自由振动频率由刚度比平方根控制的结论。
自然频率 = (1)
实验上,我们可以(原则上)建立一个单自由度系统,由弹簧上的刚性块组成。如果我们把它推下去并释放它,我们会发现位移对时间是一个单频率的正弦函数,这相当于方程1所预测的自然频率,如图2所示。
然后我们可以添加一个与弹簧平行的粘性阻尼器,并提供一个如图3所示正弦力。通过仔细地施加频率逐渐增加的恒定振幅正弦力并记录运动的振幅,我们就能生成弹簧-质量-阻尼器系统的经典归一化频率响应。通过反复使用各种阻尼器的测试,可以得出如图4所示的经典频率响应。假设我们知道系统的质量、刚度和阻尼,这个响应也可以用方程2所示的运动微分方程的标准频域解进行很好的预测。
图2.简单弹簧-质量系统的自由响应
振幅= (2)
图3.带有强迫力的简单弹簧-质量-阻尼器系统
图4.弹簧质量阻尼器系统对等幅力的频率响应
关于这些频率响应有几个值得注意的地方。第一种是在低激励频率下,响应振幅大致恒定且大于零。振幅由施加的力与弹簧刚度的比率决定。第二个是,响应增加到一个峰值,然后在低和中等阻尼情况下迅速下降。
这个峰值频率大约是阻尼自然频率(从技术上更正确的说,它是峰值响应频率,随着衰减的增加,衰减频率从阻尼自然频率向下移动)。 当激励频率与阻尼固有频率相匹配时,系统被称为“共振”。 当激励频率接近这个频率时,可能有非常大的振幅。振幅由阻尼的大小控制(更多阻尼减小振幅)。 高阻尼情况下没有真正的峰值,并被称为“过阻尼”。最后,所有更高频率的振幅继续下降。 这些特性将与后面章节中旋转系统对不平衡激励的响应形成对比。
从简单的单质量系统到多质量系统,基础不改变。自然频率仍然主要与质量和刚度有关,并且由于阻尼而有一些变化。激励频率等于阻尼的固有频率是共振。共振附近的激励可能导致大振幅响应。响应振幅由阻尼控制。阻尼足够大,可以完全消除响应峰。最大的变化是,现在有多个自然频率,每一个固有频率都有一个对应的独特的“振型”,其中结构的不同部分以不同振幅和不同相位彼此振动。
实际结构可以看作是一系列更精细、更精细的集中质量近似,它们接近连续的质量分布。连续结构具有无穷多个固有频率,每个固有频率都有自己的特征振动形状(模式)。
举个例子,考虑一个简单的梁结构,在每一端由销接头支撑。 这种结构非常简单,可以实现对固有频率和振型的封闭解决方案。 等式3给出了固有频率的结果方程,前三种振型如图5所示。
f = (3)
图5.钉固梁的前三种振型
从本质上讲,这个方程仍然是刚度与质量之比的平方根,图5和整篇文章中所示的模式形状为给定(阻尼)固有频率的最大位移位置梁的形状。虚线显示了在振动周期中梁的位置。这些中间位置在图的其余部分没有显示。
当所有这些背景和直觉进入旋转机械的世界时,都会有一些重要的区别,特别是一旦转子开始旋转。
简易旋转机械
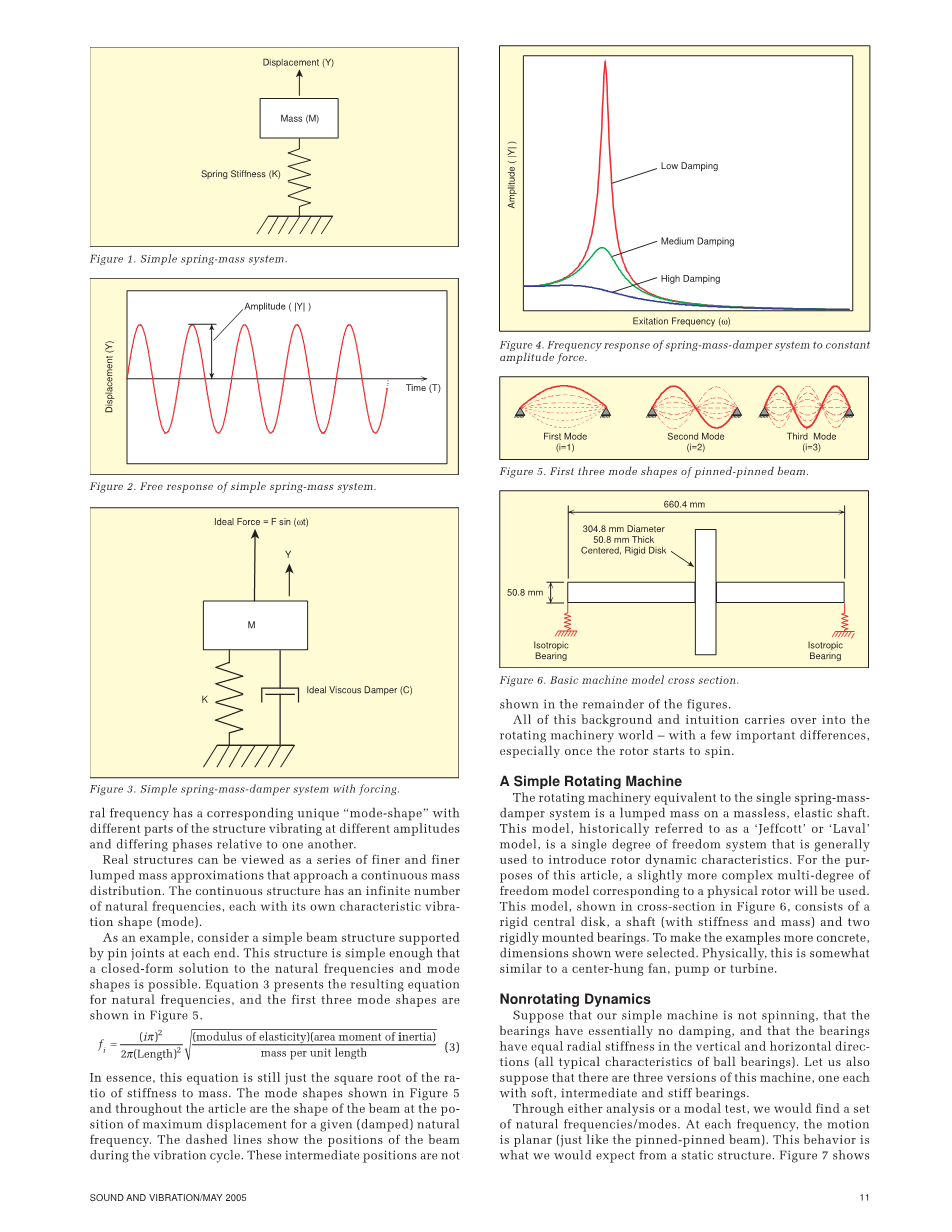
与单弹簧-质量-阻尼系统等效的旋转机械是在无质量、弹性轴上的集中质量。这个模型,历史上被称为“Jeffcott”或“Laval”模型,是一个单独的自由度系统,通常用于介绍转子的动态特性。为了本文的目的,将使用与物理转子相对应的稍微复杂的多自由度模型。该模型如图6所示,由刚性中央盘、轴(刚度和质量)和两个刚性安装的轴承组成。为了使示例更加具体,我们选择了显示的维度。从物理上讲,这与中心悬挂的风扇,泵或涡轮机有些相似。
图6.基本机器模型横截面
非旋转动力学
假设我们的简单机器不旋转,轴承基本上没有阻尼,并且轴承在垂直和水平方向上具有相同的径向刚度(球轴承的所有典型特性)。 我们还假设该机器有三个版本,每个版本都有软轴承,中间轴承和刚性轴承。
通过分析或模态测试,我们可以找到一组固有的频率/模式。 在每个频率下,运动是平面的(就像固定的梁一样)。这种行为是我们希望从静态结构中获得的。 图7显示了三种轴承刚度的前三种振型和频率。 与梁一样,粗线表示最大位移时的轴中心线形状。 当它振动时,它从这个位置移动到未移位的中心线对面的相同位置,然后返回。
图7.模态形状与轴承刚度,轴不旋转
图8.轴以10 rpm的转速旋转,第一振型和频率以rpm为单位
注意轴承刚度与轴刚度之比对模态振型有显著影响。对于软轴承和中间轴承,轴在较低的两种模式下不太弯曲。因此,这些通常被称为“刚性转子”模式。随着轴承刚度的增加(或轴刚度减小),轴弯曲量增加。
模式形状的一个有趣特征是中心盘如何移动。 在第一种模式下,磁盘平移而不摇摆。 在第二种模式下,它没有平移而摇摆。 随着频率的增加,这个一般特征会重复出现。 如果我们将磁盘偏离中心,我们会发现运动是平移和摇摆的混合。 一旦轴开始旋转,这个特性会引起一些有趣的行为。
如果我们重复等幅激励频率扫描实验,我们将会得到与前面所示的弹簧-质量-阻尼系统图相似的行为。在低频时,会有一个弹簧控制的偏转,振幅的峰值,振幅随频率的进一步增加而衰减。
旋转动力学 - 圆柱模式
由于旋转机械必须旋转来做有用的工作,让我们考虑一下当转子旋转后的第一种模式会发生什么变化。再者,随着轴承刚度的增加我们将有三个不同的版本,我们将假设我们的支撑轴承在所有径向方向都有相同的刚度。让我们以轴每分钟10转的转速重复我们的分析/模态测试,并观察最低固有频率的频率和模式形状。下面的图8显示了这三种机器的最低模式的频率和模式形状。
注意到运动的形状已经改变。 不过,频率非常接近非旋转第一模式。 与非旋转情况一样,轴刚度与轴刚度比对振型有很大影响。 同样,几乎没有轴弯曲的情况被称为刚性模式。 这些模式看起来非常像非旋转模式,但它们现在涉及圆周运动而不是平面运动。 为了想象转子如何移动,首先想象一下摆动跳绳。 绳索沿着圆柱体的轮廓运动。 因此,这种模式有时被称为“圆柱形”模式。 从前面看,绳子似乎在上下跳动。 因此,这种模式有时也被称为“反弹”或“平移”模式。
然而,与大多数跳绳不同,转子本身也在旋转。转子的旋转运动(#39;跳绳#39;运动)可以与轴的旋转方向相反,也可以与轴的旋转方向相反。这就产生了“正向旋转”和“反向旋转”的标签。图9显示了同步正向和同步反向旋转时的转子横截面。注意到,对于正向旋转,转子表面上的一个点与旋转方向相同。因此,对于同步正向旋转(如不平衡激励),转子外部的一个点保持在旋转轨道的外部。另一方面,在反向旋转的情况下,转子表面的一个点在旋转过程中与旋转轨道内部的旋转方向相反。
图9.旋转感
为了了解更大范围的轴转速如何改变这种情况,我们可以进行轴转速从不旋转到高速旋转范围内的分析/模态测试。然后我们可以记录与第一种模式相关联的正向和反向频率。图10绘制了在较宽的轴转速范围内的正向(红线)和反向(黑色虚线)的自然频率。这个图通常被称为“坎贝尔图”。从这个图中我们可以看到,这个圆柱模式的频率在整个速度范围内变化不大。反向旋转模式稍微下降,正向旋转模式稍微增加(在高刚度情况下更明显)。 这种变化的原因将在下一章节中探讨。
图10.运行速度对第一模式的影响
旋转动力学-圆锥形模式
既然我们已经探索了圆柱模式,让我们看看第二组模式。图11显示了三台机器的下一个频率和振型。频率接近磁盘摇摆而不平移的非旋转模式。这个模式看起来很像非旋转模式,但又涉及圆周运动而不是平面运动。
图11.轴以10 rpm的转速旋转,第二振型频率以rpm为单位
为了观察转子是如何运动的,想象一下在中心拿着一个拉杆固定器,然后移动它,使两端分别出现两个圆圈。杆的轨迹是指向杆中心的两圆锥体的轮廓。因此,这种模式有时被称为“圆锥”模式。从侧面看,棒看起来是围绕中心上下摆动,左侧与右侧不同步。因此,这种模式有时也被称为“摇滚”模式或“音调”模式。与第一模式和非旋转模式一样,低轴承刚度模式通常称为刚性模式,并且高的轴承刚度拉入转子端部。与圆柱模式一样,旋涡可以与转子的旋转方向相同(“正向旋转”)或相反(“反向旋转”)。
要观察轴速度变化的影响,我们可以再次进行从非旋转到高旋转速度的分析/模态测试,并记录与锥形模式相关的两个频率。 图12绘出了在很宽的速度范围内的正向(红线)和反向(黑色虚线)固有频率。 从这个图中我们可以看出,锥形模式的频率在整个速度范围内都有所改变。反向模态频率会下降,而正向模态的频率增加。
图12.运行速度对第二固有频率的影响
这种令人惊讶的行为的解释是,每当振型有一个角(锥形/摇摆)分量时,就会产生陀螺效应。首先考虑正向旋转。随着转轴速度的增加,陀螺效应基本上起到使中心盘上做摇摆运动的弹簧越来越硬的作用。增加刚度可以增加固有频率。对于反向旋转,作用是相反的。增加转子旋转速度可以降低有效刚度,从而降低固有频率(作为一个侧面说明,陀螺的术语通常是作为一个斜对称矩阵加到阻尼矩阵上的),但最终的结果是一种加强/软化效应。
在圆柱模态的情况下,由于中心圆盘只旋转而没有任何圆锥运动,所以陀螺效应的影响很小。没有圆锥运动,陀螺效应就不会出现。因此,对于具有圆柱形运动的软轴承的情况,没有观察到任何影响,而对于刚性轴承情况,它有一个膨胀的圆柱体(在轴承附近有圆锥型运动),有轻微的影响。
探索陀螺和质量效应
既然我们已经知道了当运动有一些锥形分量时,陀螺效应是如何改变旋转固有频率的,让我们看看两组单个的圆盘转子。在每种情况下,都会有一个标称转子、一个重盘转子和一个直径较小、更长的圆盘转子。重磁盘与标称值的不同之处在于,附加了等于磁盘质量的虚拟质量(即质量增加,但质量惯性矩不变)。较小的较长磁盘的重量相同,但直径较小,长度更大。这个较小的圆盘减少了围绕旋转轴的质量惯性矩(“极性”力矩Ip)0.53倍,并且将围绕盘直径的质量惯性矩(Id)减小了0.65倍。
对于第一种情况,让我们再次使用对称的中心磁盘转子。图13显示了三种模型,以及三组自然频率与速度的关系。将标称模型与两个修改后的版本进行比较,请注意:
1. 增加的质量降低了第一种模态的频率(质量是在一个大的旋转运动的点)。
2. 增加的质量使第二模态保持不变(增加的质量处于小的旋转运动的点)。
3. 减少质量惯性矩不改变第
全文共11244字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[10685],资料为PDF文档或Word文档,PDF文档可免费转换为Word


