英语原文共 13 页，剩余内容已隐藏，支付完成后下载完整资料

---

国际疲劳杂志 28（2006）1739–1751

国际疲劳

杂志

www.elsevier.com/locate/ijfatigue

液压缸的实际疲劳分析和一些设计建议

I.Marczewska ^a, T. Bednarek ^a, A. Marczewski ^a,*, W. Sosnowski ^a,H.Jakubczak^b,J.Rojek^a

波兰科学院基础技术研究所，ul。Swietokrzyska 21，00-049 华沙，波兰

理工大学汽车与工程机械工程学院，工程机械工程学院，ulNarbutta 84，02-524华沙波兰2005 年 7 月 7 日收到；2005 年 11 月 21 日收到修订本；

2006 年 1 月 4 日接受可以在线使用 2006 年 3 月 7 日;

摘 要

在本文中，提出了一种数值算法，该算法可以将手头特定结构（例如液压缸）的不同加载方案用特定沃勒曲线表征给定材料的抗疲劳性。本文中使用的模型是基于参考文献[S.Oller，O.Salomon，E.Onate，A continum mechanics model for mechanical fatigue analysis Comput Mater Science2005;32(2)：175-95]。分析了在 E.C. 项目“ PROHIPP”下研究的液压缸，并提出了解决油口区域裂纹问题的一些解决方案。必须对载荷下的气缸进行计算，这与沃勒曲线中提供的实验数据有所不同。进行一些设计更改后，就可以消除机油端口连接区内的机油渗透。正如在EN13445规则说明（第18I点）末尾所写的欧洲规范EN13445。单燃压力容器,第18章:疲劳寿命的详细评估，http://www.unm.fr/en/general/ en13445/default.htm]，基于有限元分析和疲劳数据的应力分析“结合”仍然是当前 EN 13445的不足之一,我们认为本文可以减少部分这种不足。

copy;2006 ElsevierLtd。保留所有权利。

关键字：耐力极限；液压缸；沃勒曲线；古德曼图

1. 介绍

本文有两个目标。第一个目的是提出一种数值算法，采用不同的液压缸加载方案，以特定的Wohler曲线表征给定材料的抗疲劳性。为了找出古德曼曲线与沃氏曲线参数之间的关系，对单轴加载情况进行了研究。第二个目标是 本文研究了在E.C.项目“PROHIPP”下液压缸的计算，并提出了油口区裂纹问题的解决方案，以消除油在油口区中的渗透。

本文所使用的模型是基于参考文献中描述的特定模型的特殊应用。[1].

作者电话： 228261281X147传真： 48228269815

电子邮件地址：asmar@ippt.gov.pl(A.Marczewski).

0142-1123 / 见前件?2006 Elsevier Ltd.保留所有权利。

doi:10.1016/j.ijfatigue.2006.01.003

众所周知，大多数疲劳试验都是针对对称或几乎对称的载荷进行的，在这种情况下

（1）

计算机编码数只接受这种对称负载的输入数据。实际上，大多数结构（例如液压缸）都是在复杂得多的循环荷载作用下工作的，由不同的R值组成。特别是，当应力从0变为某些特定的最大值时，对R=0进行了典型的实验室测试。液压缸的情况就是这样，通常以这种方式测试，其中外部压力施加到缸体，然后压力被移除。

I.Marczewska等人/《国际疲劳杂志》28（2006）1739-1751

引入等效振幅应力，求出平均应力比R不等于-1的载荷失效循环次数（参见等式 1）。当实验测试数据提供沃勒曲线时，仅为R=-1的值。

这种试验的循环次数取决于气缸最弱点的疲劳抗性。这类点（例子如油端口）其焊接残余应力、局部剪切力和油在连接间隙中的渗透而产生的力会引起疲劳裂纹，从而导致最终的破坏。

进行两种数值试验。首先，对工件进行了标准疲劳试验，如图（5）（第3节）所示。采用适当的的沃勒曲线：R =-1 的对称载荷和 R = 0 的非对称载荷，用典型的材料特性来生成两种不同载荷方案。使用古德曼曲线和经典沃勒曲线来计算达到疲劳极限的循环次数。

接下来，在第四节中考虑了液压缸的疲劳问题。油口的典型变形和可能的设计修改如图（16）所示，可以观察到油口连接区的油口与缸体之间的间隙随着油压的增加而增大。此外，实验（图16）确认焊缝在此连接区的裂纹敏感性。作者建议通过使用特殊的垫圈或胶水来改善这种不良情况，以消除油口与缸体表面之间的过度间隙。这种垫圈或胶水可以防止渗透，从而消除了相邻焊缝过早疲劳裂纹的可能性。

由于油口的焊接过程，垫圈或胶水材料应该是耐高温的。

在本文中，用公式计算的一维极限冯米塞斯应力来表示用三维有限元结构模型计算的应力场

以便用于一维疲劳分析，分量S_X、Sy、Sz是给定x、y和z方向上的应力值。Sxy、Syz、Szx是剪切应力。

2. 沃勒和古德曼曲线的依赖性

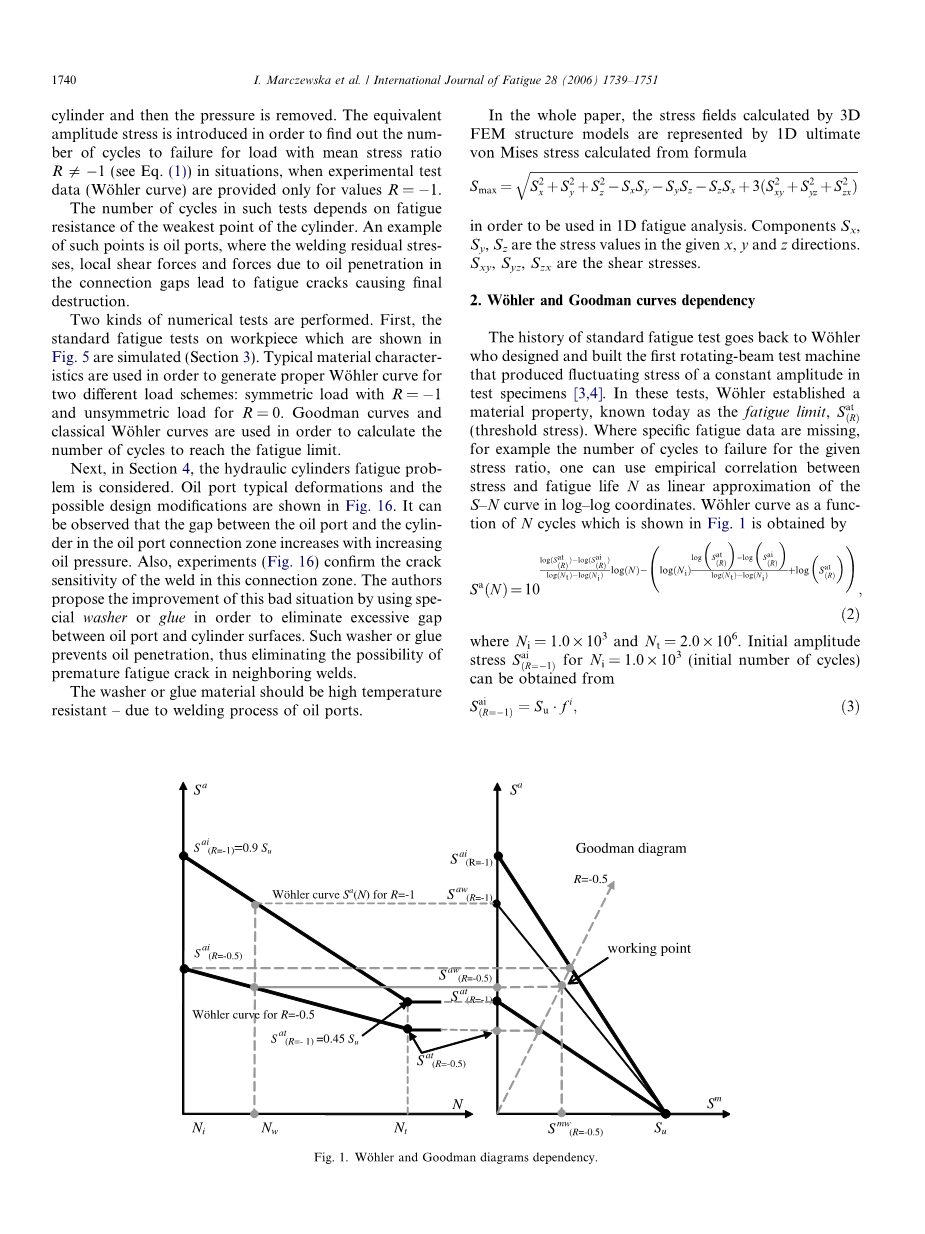
标准疲劳试验的历史可以追溯到Wohler，他设计并制造了第一台旋转光束试验机，在试验试样中产生恒定振幅的波动应力[3，4]。在这些试验中，Wohler建立了一种材料特性，今天被称为疲劳极限（阀值应力）。在缺少特定疲劳数据的情况下，例如：给定应力比和失效循环的次数，可以利用应力与疲劳寿命N的相关性作为对数坐标画出S-N曲线。沃勒曲线作为N个循环的函数，如图1所示是通过以下等式

（2）

其中N_i=1.0X10³和N_t=2.0X10⁶。对于初始循环次数为N_i=1.0X10³的初始振幅应力可从公式获得 （3）

I.Marczewska等人/《国际疲劳杂志》28（2006）1739-1751

其中fi是对应于N_i =1.0X103循环周期的应力减小因子,在文献[1，3，5，6]中可以找到fⁱ 的值。在本文中等于0.9。阀值振幅的应力值是以N_t=2.0X10⁶（最低周期数）通过下列公式计算的计算的

i

（4）

其中ft是阈值应力对应的应力下降因子。ft值在0.05 和0.5之间变化，取决于材料性能和应力集中系数[1,3，5，6]，本文中ft等于0.45。

取，其中W代表工作点，通过转换方程（2），我们可以通过振幅应力S^aw得到失效循环次数Nw

（5）

其中标准的S-N（Wohler曲线）见图(1)左，是基于振幅应力S=Sa或最大应力S=Smax

通常，通过旋转弯曲疲劳试验或轴向载荷试验（R=0），得到完全反向应力（R=1）的Wohler曲线。然而这种0或1的平均应力对于在循环载荷下工作的实际工业部件来说并不典型。

根据极限应力S_U值和振幅应力值，我们可以从Goodman图中得到振幅应力的值（见图1右）。

古德曼线用线性方程表示

（6）

如果平均应力Sm的值等于0（R=-1），则得到S=S。平均应力Sm值是从

(7)

根据方程（6）中得到了R=1的应力幅值。

（8）

由方程（8）计算的振幅应力值可以替换为等式（5），其中=，通过任意非对称的载荷和任意应力比计算被分析结构失效的周期数。

2.1.任意选择的参数R 对S- N 函数的影响

在对数标度中，Wouuml;hler曲线可以表示为振幅应力S^a与失效N的循环数之间的关系。引入沃勒曲线的不同方法是它作为最大应力S^max与失效周期数之间的关系，在第5节中使用S^max和S^a来最终计算N到失效的周期数。本文提出了两种计算的方法。构造沃勒曲线（N）方程式依靠下文介绍的。

(9)

我们从依赖关系中得到的R的不同值的应力最大值是

(10)

其中R的不同值的振幅应力S由下式给出：

通过将Sm表示为函数Sa和R得到（见方程式（6)）。

对于R的任意值，也可以得到最大应力S

(11)

在论文[1]中给出。S是一个需要确定的参数。确定此参数的方法将在下一小节中介绍。基于R 比的实际值和耐力应力的基本值（R=1的门阈 应力），文章[1]的作者假设了Wohler曲线（N）（比较方程式（2））给予的R值作为指数函数。

(12)

其中ALFAF、AUXR1和BETAF是数值代码COMET[5]中使用的疲劳参数。确定特定材料和不同负载方案（R）参数的方法将被介绍在下一小节。

方程式（2）表现接近疲劳分析的“经典” Wohler方法。方程式（12）取自COMET[1，5]， 并考虑了不同的疲劳破坏模型。当比较图时， 可以看到两种模型图1（经典的沃勒）和图4（COMET[1，5]）之间的差异。这两种模型：一种从古德曼图和“经典”沃勒曲线开始，另一种从参考文献开始。[1]已被用于对照实验验证计算。

正如在EN13445规则描述的末尾（第18章第18I点）[2]所写的那样，从有限元和疲劳数据进

I.Marczewska等人/《国际疲劳杂志》28（2006）1739-1751

行应力分析的“ 联 姻 ”仍是当前EN13445的不足之处之一 。我们认为本文一定程度上减少了这一缺陷。

3.数值例子

3.1沃勒和古德曼曲线相关性针对特定材料和不同的载荷方案（R）的应用

在本节中，对于一些特定的材料，提出确定数值代码COMET[5]中使用的疲劳参数值的一个例子（ALFAF、AUXR1、BETAF等）。疲劳参数建立在沃勒曲线上，通过方程式(12)给出符合和的点。将从方程式（9）和（11）确定和的值。在第4节和第5节中使用了和的值和疲劳参数，以最终计算失效周期数N。

从方程（9）中确定和，我们必须首先计算和的值。因子应力f^t和fⁱ的值（见方程式（3）和（4））需要取得来自文献初始和阈值的振幅应力（R=-1）。从方程（3）中得到了N_i=1.0X10³的初始振幅应力。

从方程（4）中得到了N =2.0X106的门阈振幅应力S值

对于R不等于1的不同值，需要用方程（10） 计算初始和门阈振幅应力。例如，对于给定的R=-0.5和N_i=1.0X10³，从下面式子获得振幅应力

不同R值的初始和阈值振幅应力的值如表（1）和图（2）所示。

从方程中（7）计算出不同R值的平均应力如表（2）所示。例如：R=0.5的初始平均应力等于

从方程（9）中得到不同R值的最大应力如表3所示。例如，R=0.5的初始最大应力等于

I.Marczewska等人/《国

剩余内容已隐藏，支付完成后下载完整资料

---

资料编号：[421264]，资料为PDF文档或Word文档，PDF文档可免费转换为Word

您可能感兴趣的文章

• 现代单元结构在压缩载荷作用下的影响外文翻译资料
• 水下浇口凸轮衬套注塑模设计与分析外文翻译资料
• 机械微机械加工的最新进展外文翻译资料
• 考虑尺寸效应的物料流动特性建模外文翻译资料
• 智能移动机器人的无人监督人体活动分析外文翻译资料
• 手臂的视觉感知操纵着触觉的体验快感外文翻译资料
• 稀土元素对6061铝合金真空钎焊接头组织和性能的影响外文翻译资料
• 定向凝固铝硅镁共晶合金的组织、力学和电学特性研究外文翻译资料
• 机床进给传动装置外文翻译资料
• 数控机床工业设计方法的研究及其实现和应用前景外文翻译资料