
英语原文共 32 页,剩余内容已隐藏,支付完成后下载完整资料
三角洲打印硬件
三角洲打印机设计,轴排列方式与笛卡尔打印机截然不同,但使用的基本硬件与笛卡尔打印机相同。例如,步进电机、电子板甚至热端也没有什么特别的,不同的是轴的排列方式(所有三个轴都是垂直的)。打印床通常是圆形的(较旧的设计使用方形或矩形生成曲面),框架通常是三角形的。仅这些品质就使三角洲打印机具有独特的垂直形式,占用空间小。
bull; 注意 Internet lore2 通过三角形或棱镜框架形状定义三角洲打印机。但是,并非所有三角洲
打印机都有该形状。有些圆柱形框架比棱镜更像圆柱体,早期的设计采用了矩形框架。
在本章中,您可以发现三角洲打印机的工作原理; 三角洲打印机的构造方式,包括框架、轴、电子装置的所有组件等等。您还将查看三角洲打印机设计的一些变体。虽然所有三角洲打印机设计都具有相同的轴排列,但它们的构造方式可能有很大差异。例如,框架的范围从附加到木件的印刷部件、由木材制成的整个框架、包含铝挤压柱的贴有木材或印刷部件的相框,以及塔的光滑杆。在了解有关硬件的更多内容之前,让我们看看三角洲打印机的工作原理。也就是说,它如何解决将热端定位到生成卷中的特定位置。
三角洲打印机剖析
在本节中,我从组件作为整体的一部分的工作方式的角度探讨构成三角洲打印机的组件。我将在下一节中讨论构成这些组件的硬件。了解组件的工作原理将更好地了解打印机的构造方式。这不仅有助于您更好地了解打印机,还可以帮助您在决定构建自己的三角洲打印机时提供帮助。
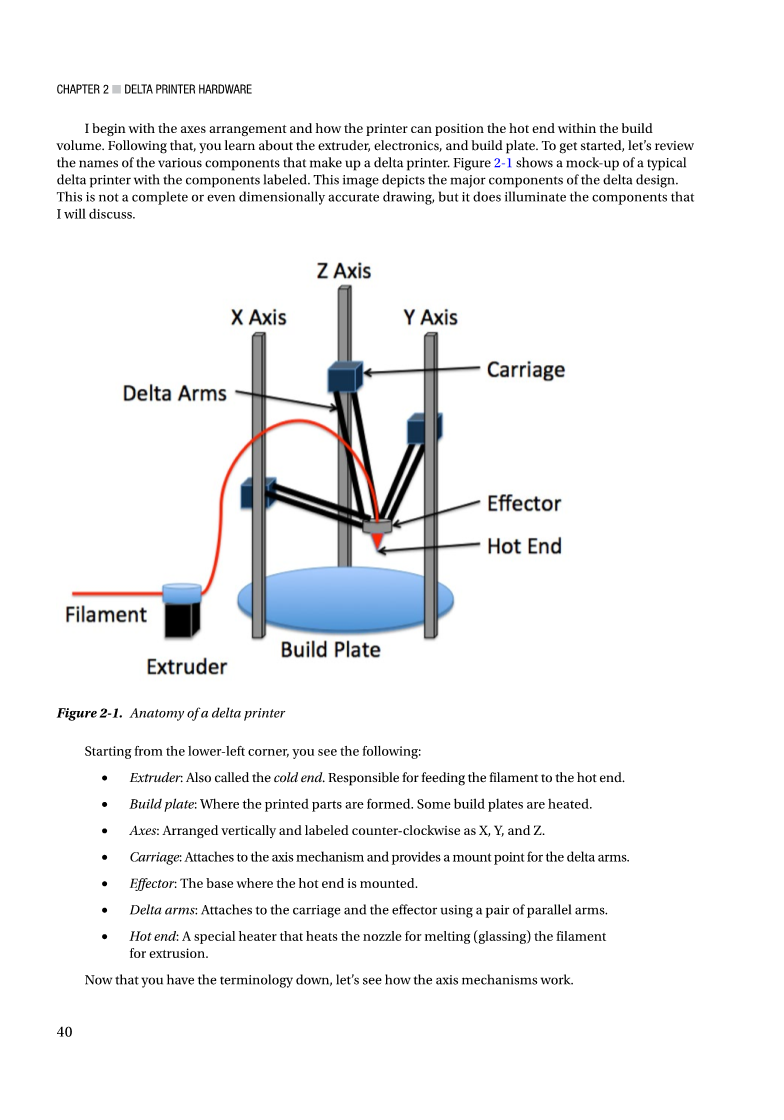
我首先从轴排列以及打印机如何将热端放置在生成卷中。之后,您将了解挤出机、电子装置和构建板。开始让我们查看组成三角洲打印机的各种组件的名称。图 2-1 显示了带有标记组件的典型三角洲打印机的模型。此图像描绘了三角洲设计的主要组件。这不是一个完整甚至尺寸精确的绘图,但它确实照亮了我将讨论的组件。
图 2-1。三角洲打印机的剖析
从左下角开始,您将看到以下内容:
挤出机:也称为冷端。负责将灯丝送入热端。
构建板:形成打印零件的位置。有些建筑板被加热。
轴:垂直排列,逆时针标为 X、Y 和 Z.
滑车:附加到轴机构并为三角洲臂提供安装点。
效应器:安装热端的底座。
三角洲臂:使用一对平行臂连接到滑车和效应器。
热端:一种特殊加热器,用于加热喷嘴以熔化(玻璃)用于挤压的灯丝。
轴
每个轴都安装在垂直方向上。滑车安装在轴运动上,形成平行臂的一侧,将滑车连接到效应器。因此,当轴上下移动时,滑车将随之移动。
回想一下,三角洲臂、效应器和轴运动的组合形成了一个直角三角形,如图 2-2 所示。在这里,您可以看到三角洲臂形成由垂直轴形成的直角三角形和从轴到效应器的虚线。
请注意,您还必须考虑两个偏移量。从轴运动的中心到滑车上的三角洲臂的安装点有一小段距离。还有一段短距离,是从效应器上的三角洲臂安装点到热端的喷嘴中心。因此,任何计算在定位效应器时也必须考虑这些测量值。
图2-2。三角洲几何学
bull; 注释图 2-2 仅显示一个轴,但定义的测量值和角度在所有三个轴上都相同。
那么,打印机(固件)如何确定使用此数据定位效应器的位置?由于轴、三角洲臂和效应器形成直角三角形,因此可以巧妙地使用三角方程。 通过此信息,您可以计算移动一侧 (B) 以移动效应器(侧 A)的量。在这种情况下,您知道斜点的长度始终相同(三角洲臂),因此,要计算移动,请使用公式,使用平方和计算直角三角形的边。
但这只是所需计算的一半。您还需要了解每个塔相对于彼此的位置。如果您设想从打印机顶部向下看,则坐标轴位于如图 2-3 所示。请注意叠加在构建板上的假想三角形形成的角度。如果您认为三角洲臂形成平行四边形,则可以稍微简化数学,因此只需计算表示每对手臂中心的三角。
请注意,形成的三角形允许您知道塔彼此之间的关系。事实上,一旦您知道每个塔相交形成的圆的半径(也称为三角洲半径),就可以使用主数和后方函数计算每个塔的位置。清单2-1摘自马林固件(位于配置.h)。
清单2-1。计算塔的位置
#define DELTA_TOWER1_X -SIN_60*DELTA_RADIUS // front left tower
#define DELTA_TOWER1_Y -COS_60*DELTA_RADIUS
#define DELTA_TOWER2_X SIN_60*DELTA_RADIUS // front right tower
#define DELTA_TOWER2_Y -COS_60*DELTA_RADIUS
#define DELTA_TOWER3_X 0.0 // back middle tower
#define DELTA_TOWER3_Y DELTA_RADIUS
在这里,您可以看到,Marlin 固件使用 Y 塔作为计算的起点(任意赋值,因为任何源的计算都是相同的)。
现在,您已经了解了每个塔相对于彼此的位置,因此可以使用塔的位置、每个轴的原始位置以及要移动的位置的笛卡尔位置来计算任何移动。清单2-2显示了马林固件(位于Marlin_main.cpp)的计算。
清单2-2。计算三角洲运动空隙
calculate_delta(浮标点菜[3])
{
delta[X_AXIS] = sqrt(DELTA_DIAGONAL_ROD_2
- sq(DELTA_TOWER1_X-cartesian[X_AXIS])
- sq(DELTA_TOWER1_Y-cartesian[Y_AXIS])
) cartesian[Z_AXIS]; delta[Y_AXIS] = sqrt(DELTA_DIAGONAL_ROD_2
- sq(DELTA_TOWER2_X-cartesian[X_AXIS])
- sq(DELTA_TOWER2_Y-cartesian[Y_AXIS])
) cartesian[Z_AXIS]; delta[Z_AXIS] = sqrt(DELTA_DIAGONAL_ROD_2
- sq(DELTA_TOWER3_X-cartesian[X_AXIS])
- sq(DELTA_TOWER3_Y-cartesian[Y_AXIS])
) cartesian[Z_AXIS];
如您所见,固件计算所有三个轴的位置。这样,打印机可同时移动所有三个轴以重新定位热端。很酷吧?
在计算每个轴的位置时要多加一点。如果打印机支持自动平层(Z-probing),则在这些操作之后会执行其他计算以优化位置。更不用说对托架、效应器和热端偏移所做的调整了。但是,对于我们的讨论,请将这些计算视为负责定位效应器的计算。
让我们看一个计算示例。在此示例中,您可以将打印机定位到笛卡尔值 [0,0,0],并且希望将执行器移动到位置 [-40,20,15]。此外,您还希望了解前面的计算是如何解析为三个轴的移动。我使用 Kossel Pro 打印机作为示例,但您可以使用您自己的三角洲打印机。但是,如果您正在构建打印机,或者尚未配置或校准打印机,则可能需要阅读接下来的两章,然后返回到本章练习;或只是跟着我演示数学。
首先将热端移到床中心位置。您可以使用打印机控制器软件或 LCD 执行此操作。接下来,使用一小段遮蔽或蓝色油漆的胶带,并标记塔上每节车厢的位置。图 2-4 显示了在打印机上标记 X 塔的示例。确保放置磁带,使其不会干扰轴移动。
图 2-4。标记滑车位置
注意 虽然并非纯科学,但以下将演示这些计算如何解决每个轴的位置,以影响生成卷中的移动。
接下来,将效应器向左移动 40 毫米(X = 40)和向前移动 20mm (Y = 20),然后将效应器提升 15 毫米(Z = 15)。一旦到位,测量每个轴移动的距离。不要担心准确,因为这不是一个科学测试,而是一个演示。图 2-5 显示了我如何测量其中一个轴。
塔和轴命名
笛卡尔打印机中,每个轴在单个平面中分别移动。因此,简单地指轴在 X、Y 或 Z 方向上的每个移动是正确的。但是,在三角洲坐标系中,每个轴都是垂直方向的,因此 X 轴和 Y 轴机制不会在同一平面中移动。只有 Z 塔可以在同一平面上考虑。但这也不正确。回想一下,它需要从所有三个轴移动才能在 X、Y 和 Z 平面中执行移动。因此,您将每个轴运动称为 A、B 和 C 或 Alpha、beta 和 Gamma,对应于 X、Y 和 Z 塔。您可能会发现一些三角洲文献,这些称为 a、B 和 C 塔。在测量轴运动而不是效应器的位置时,将轴移动称为A、B 和 C。
图 2-5。测量轴移动
当我测量我的塔时,我发现以下内容:
X塔 (A) = 25.5 毫米
Y塔 (B) = -17 毫米
Z塔 (C) = 23 毫米
注意我使用的符号。当轴'向上移动'时,它正朝着正方向移动。因此,如果滑车位于标记上方,则测量该值为正值;当滑车低于标记时,您将将其测量为负值。
现在让我们做数学,而不是手工解决方程,我写了一个简短的Python脚本来执行计算。清单2-3显示了我创建的代码。你可以从apress.com/9781484211748?gtmf=s下载这本书的源代码。我稍微简化了代码,以便更容易阅读,但计算与前面的计算完全相同。
Listing 2-3. Cartesian to Delta Simulation
import math import argparse
DELTA_DIAGONAL_ROD = 300.0
DELTA_SMOOTH_ROD_OFFSET = 212.357
DELTA_EFFECTOR_OFFSET = 30.0
DELTA_CARRIAGE_OFFSET = 30.0
DELTA_RADIUS = (DELTA_SMOOTH_ROD_OFFSET-DELTA_EFFECTOR_OFFSET-DELTA_CARRIAGE_OFFSET) DELTA_PRINTABLE_RADIUS = 127.0
DELTA_CARRIAGE_OFFSET) DELTA_PRINTABLE_RADIUS = 127.0
CHapter 2 Delta prInter HarDware
SIN_60 = math.sin(math.pi/3)
COS_60 = 0.5
DELTA_TOWER1_X = -SIN_60*DELTA_RADIUS
DELTA_TOWER1_Y = -COS_60*DELTA_RADIUS
DELTA_TOWER2_X = SIN_60*DELTA_RADIUS
DELTA_TOWER2_Y = -COS_60*DELTA_RADIUS
DELTA_TOWER3_X = 0.0
DELTA_TOWER3_Y = DELTA_RADIUS
DELTA_DIAGONAL_ROD_2 = (DELTA_DIAGONAL_ROD*DELTA_DIAGONAL_ROD)
Z_MAX_POS = 280.67
X_AXIS = 0
Y_AXIS = 1
Z_AXIS = 2
delta= [0.0,0.0,0.0]; current_pos = [0.0,0.0,0.0] difference = delta
parser = argparse.ArgumentParser(description=Provide Cartesian coordinates.)
parser.add_argument(source, nargs=3, type=float,
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[236385],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


