啸叫噪声幅度的模型与减弱外文翻译资料

英语原文共 15 页，剩余内容已隐藏，支付完成后下载完整资料

啸叫噪声幅度的模型与减弱

Paul A. Meehan^a , Xiaogang Liu^b

(a昆士兰大学，澳大利亚布里斯班,b武汉理工大学，武汉，中国)

摘要：车轮啸叫噪声的振幅和声压级预测值使用一个简洁的数学模型进行调查，该数学模型通过测量滚动接触式双盘试验台和现场案例研究得到验证。该模型用于执行基于能量的分析来确定稳态极限循环啸叫期间的蠕变振动振幅的封闭形式解决方案。该解决方案用完全非线性模型与使用实验调谐蠕变曲线的数值解比较。预测的啸叫声水平趋势也与以各种捕捉速度（与攻角成正比）记录的不同的轧制速度相比较。另外，对许多领域进行进一步的确认车轮在300米的尖锐曲线上发出啸叫声。此外，还与Rudd [1]的修改结果进行了一个简单的比较，并强调了目前有效模式准确性和优点。该解决方案分析了为什么啸叫噪声的声压水平也随捕捉速度（或攻角）的增加而增加以及振幅如何受关键啸叫参数影响，包括详细的模态阻尼的研究。最后，有效模型用于执行参数化研究实现啸叫噪声降低6 dB的手段。结果强调抓取速度（和攻角）的重要性以及蠕变曲线参数可以使用第三体（即摩擦改性剂）控制。结果与实验和实地观察结果一致并在减轻车轮啸叫和噪音的机制和量化它们的相对作用方面提供重要的理论视角。

关键词：轮子尖叫、振幅、预测建模、极限循环分析

1.引言

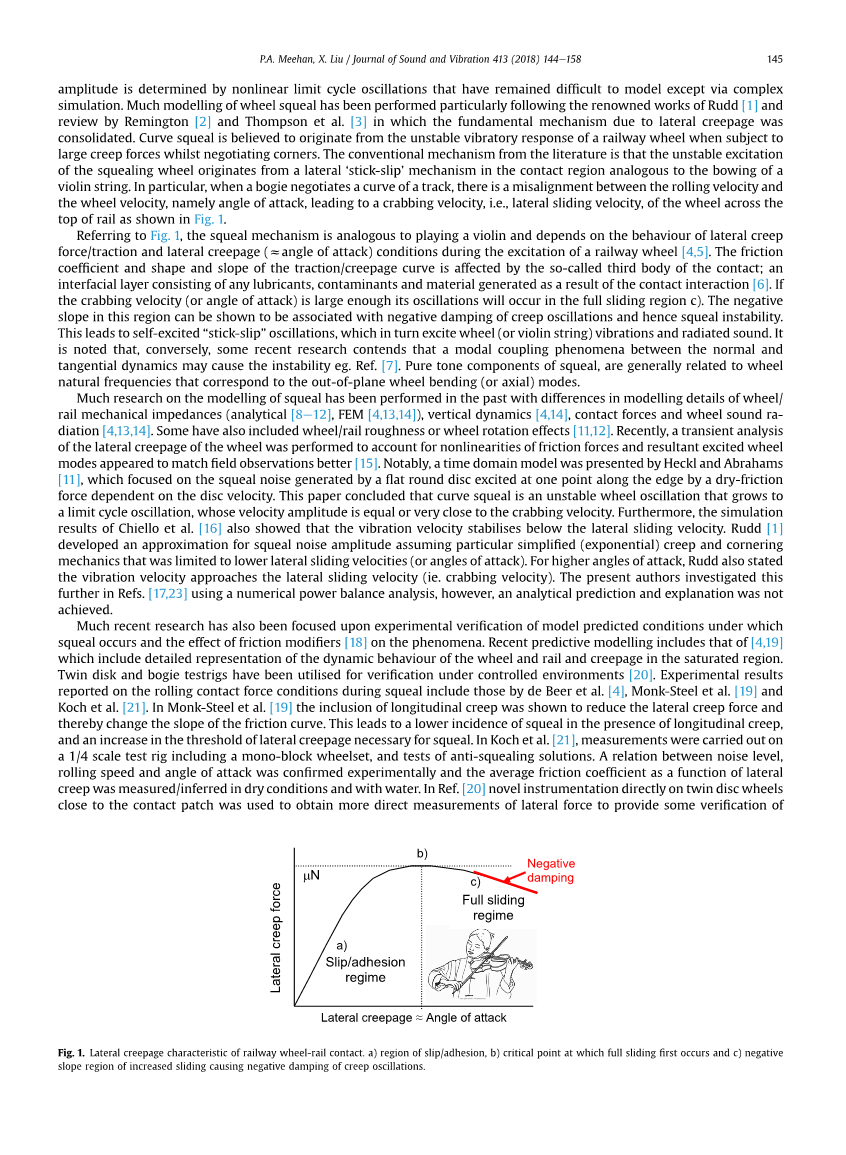
车轮啸叫是一种高调的噪声，可以在列车通过铁路线的弯道（角落）时发生。它经常发生在我们的耳朵最敏感的频率范围内，因此对于铁路附近的人是非常讨厌的。这一现象多年来一直困扰着铁路行业，随着铁路使用的不断增加和主观的人类噪声容忍度下降，这一现象已经引起了人们的高度关注。例如，在澳大利亚紧密的曲线运营中，货运铁路的影响主要来自轮子的啸叫，特别是大都市地区。尽管过去十年有很多研究得到了啸叫的机制，车轮啸叫的出现和幅度仍然表现出它的不可预测性，因为它似乎依赖于广泛的车辆和轨道参数。此外，啸叫振幅是由非线性极限循环振荡决定的，除了经由复杂模拟以外，它们仍然难以模拟。在Rudd [1]的著名作品和Remington [2]和Thompson等人的综述（由于横向蠕变引起啸叫噪声的机制在该文中还被证实）之后，已经进行了大量的车轮啸叫建模。曲线啸叫被认为起源于铁路车轮在经过弯曲轨道时由横向蠕变引起的不稳定的振动响应。文献中的传统机制认为啸叫轮的不稳定激励起源于接触区域中的侧向“粘附-滑动”机制，类似于一根小提琴弦的弯曲。特别地，当转向架通过曲线轨道时，滚动速度和速度之间存在偏差，即攻角，导致抓取速度的产生，即横向滑动速度的产生。铁路顶部的轮子产生的横向滑动速率如图1所示。

图 1 轮轨接触的横向蠕变特征

参考图1，啸叫机制类似于弹奏小提琴，受到横向蠕变力/牵引力和横向蠕变情况在列车运行时的影响。摩擦率和牵引力/蠕变曲线的形状和斜率受到所谓的接触第三体（一个界面层由润滑剂，污染物和由于接触相互作用而产生的材料组成[6]）的影响。如果抓取速率（或者攻角）足够大，此时振动将出现在完全滑动区域c。这个区域内的负斜率可以认为和蠕变振动的负阻尼有关，并因此导致不稳定啸叫。这导致了自激“粘附—滑动”振动现象，从而激起车轮（或小提琴弦）的振动和辐射声音。值得注意的是，相反，最近的一些研究认为，在正常和切向动力学影响下的模态耦合现象可能导致不稳定性，例如Ref. [7]。啸叫的纯音要素，一般都与对应于平面外轮弯曲（或轴向）模式的车轮的固有频率有关。

过去已经进行了关于啸叫建模的大量研究，其中包括轮轨机械阻抗（解析[8e12]，有限元[4,13,14]），垂直动力学[4,14]，接触力和车轮声辐射[4,13,14]，有些还包括轮/轨粗糙度或车轮旋转效应[11,12]。最近，一个车轮横向蠕变的短暂的分析是为了解释摩擦力的非线性，并发现合成激励车轮模式似乎更符合现场观测[15]。值得注意的是，Heckl和Abrahams提出了一个时域模型[11]，其侧重于研究由沿着边缘的一个点处通过干摩擦力激发的扁平圆盘产生的啸叫声，该摩擦力依赖于盘的速率。本文的结论是，曲线啸叫是一个不稳定的车轮振动，增长到极限循环振荡，它们的速度振幅与捕捉速度相等或非常接近。此外，Chiello等人[16]的模拟结果也表明，振动速度稳定在横向滑动速度以下。Rudd [1]开发了一个近似的啸叫噪声振幅模型，假设特别简化（指数）蠕变和限制在较低的横向滑动速度（或攻角）的弯曲力学。对于更高的攻击角度，Rudd也表示振动速度接近横向滑动速度（即抓取速度）。当前学者使用数值功率平衡分析在Refs. [17,23]中对此进行了进一步调查，然而，分析预测和解释未能实现。

目前已经有了许多模型预测了啸叫噪声的产生和摩擦调节器[18]的影响，许多研究已经对这些模型进行实验证实[4,19]。近来的预测模型包括在饱和区域下车轮，轨道和蠕变的详细的动态行为代表。两个圆盘和车轮已经用来在控制环境下证实这一结论[20]。de Beer et al. [4]，Monk-Steel et al. [19]和Koch et al. [21].的实验结果显示了啸叫期间的旋转接触力学情况。在Monk-Steel et al. [19]的研究中，纵向蠕变的引入揭示了横向蠕变力的减少并因此改变了摩擦曲线的斜率。这导致了在纵向蠕变的影响下一个更低的啸叫发生率和更高的啸叫噪声的横向蠕变临界值。在Koch et al. [21]中，研究人员运用了一个1/4的测试装置，这些装置包括轮副和抑制啸叫方案的测试装置。实验证实了噪音水平，旋转速度和攻角的关系，并且平均摩擦率作为一种横向蠕变的因变量在干燥情况和湿润情况下分别被测量。在Ref. [20]中，在两个圆盘上靠近接触点处的新装置被用来直接测量横向力，测试结果证实了已有的预测模型，尽管在接触点处的第三体可能会影响测试结果的准确性。在Ref. [18]中，摩擦调节器已经在欧洲的货物运输线路上抑制啸叫噪音和轮缘噪音方面已经显示出了重要作用。

尽管近来已经取得了许多成果，但是在充分理解、预测和证实啸叫噪声随着重要参数（抓取速度和攻角等）的变化趋势方面任然有许多不足。特别地，近来的模型涉及了许多复杂性来有效预测啸叫噪声幅度，并且在重要参数对啸叫噪声水平影响方面进行了详细的理论和实验调查。

目前的研究用一个简单的数学模型调查了车轮啸叫噪声的振幅和声压水平，这个模型被两个圆盘的旋转接触实验和现场测试所证实。主要的贡献包括：

1.啸叫噪声振动和噪声的极限循环幅度作为重要的啸叫参数的理论预测；

2.用实验和现场测试证实了啸叫噪声幅度趋势，并且和Rudd [1]理论的简单修改版进行了比较；

3.在为什么啸叫噪声的声压水平与抓取速率密切相关，并随着啸叫噪声的增加而增加方面提供了理论视角，同时研究了其他参数对幅度的影响；

4.通过一个对模态阻尼的影响的详细调查来实现通过重要参数的调整的识别和量化来实现啸叫噪声的减小。

该论文主要强调啸叫噪声幅度的预测和减小，这与其他论文仅仅重点强调啸叫噪声的发生不同。这篇论文将首次描述研究啸叫噪声的测试装置，实验方法和数学理论。此外，本论文也提供了啸叫的极限循环分析来获得啸叫振动和噪声幅度的闭式解，然后将这些结果与数字，实验和测试结果进行比较。最终，一个有效的模型分析了参数对于减弱啸叫噪声的灵敏度的分析。

2.理论方面

本篇论文中的实验结果已经在Ref. [24]中提到了，使用了两个旋转接触盘来研究啸叫噪声（在2.1部分进行了详尽描述）。2.2部分描述了啸叫噪声现场测试的细节。一个时域内的理论模型（Ref. [24]中提到了）在2.3部分描述到。被用来数字分析模拟的参数也源自于测试装置的特点。

2.1.实验方法

Ref. [24] 运用两个旋转接触盘来调查抓取速率对啸叫噪声的影响，正如图2所描述的那样。

图 2 旋转圆盘测试装置(a);有限元分析模型（b）

正如图2（b）所示，高低轮子之间的横向力通过应变片电桥来测量，这个方法在Ref. [22]中被详细介绍过。测试装置的参数如表1所示。

表 1 测试装置和模拟参数

高低轮之间的攻角通过Ref. [17].的方法来调整和测量。正如图2描述的那样，测试装置啸叫的声压水平通过放在低盘5cm处和距离地面80cm的扩音器记录。该记录信号被条件放大器、模数转换器、Labview软件和Matlab软件处理后设置在20 mPa RMS。声音被以2秒每次的速率记录下来，在8000Hz的样本速率下，每次抓取速率增加就记录两次。测试装置的振动特点被硬头冲击锤作用下的模态测试所测量，并且经有限元方法分析。来自有限元分析和模态测试的低轮的振动特点与声音记录结果很好地匹配，详见Ref. [17]。

2.2.现场测量

在澳大利亚网络的条件监视器记录的攻角信息（轮副相对于轨道的角度）证实了有效的啸叫噪声模型。这个系统在货运和客运火车行驶轨道上半径为300m的曲线轨道上。记录下每个经过轮子的数据包括噪音水平、AOA、横向位置和速度。正负攻角都被记录下来，结果显示负攻角显示车轮会破坏轨道，但是在这篇文章中考虑到了完全的攻角。（尽管在正负情况下都发现了类似的结果。）

车轮啸叫被观察到出现在一个宽的噪音水平，在铁路上测量的1.2m发现噪音水平从背景旋转噪音到超过115 dBA都有涉及。其他的噪音源，像轮缘噪音，机车噪音或者旋转噪音当前很少超过这个水平，因此并未排除在外。基于Ref. [29]的阐述的频谱范围，该文发展了一种简单的算法并且手动测量来从其他噪音中识别出啸叫噪声和轮缘噪声。人们普遍认为啸叫噪声是一种纯粹的音调，高频和高水平噪声，然而轮缘噪声是一种宽范围的高频噪声。通过运用这个算法，120dBA或者更高的噪音，1.2m测量，被发现排除在噪音水平之外。乘运货车不会在这个地方产生剧烈的啸叫，因此被排除在分析之外。为了比较分析预测，超过声压水平10%的通过车轮被用来现场测量。这个测量通常被用来测量交通噪音，因为它提供了一个更高极限的指示，并且已经和骚扰市民程度相匹配。据指出，尽管超过声压水平10%的过往车轮将会大体上排除非啸叫噪音，但是一些极端情况也有可能会影响现场测试数据，这将在随后讨论

全文共18671字，剩余内容已隐藏，支付完成后下载完整资料

资料编号：[13827]，资料为PDF文档或Word文档，PDF文档可免费转换为Word

您可能感兴趣的文章

• 流化床包衣造粒过程的监测与控制研究外文翻译资料
• 一种新颖的旋转流化床包衣细颗粒涂层的方法外文翻译资料
• 中国城市垃圾的处理和管理外文翻译资料
• 滤袋、气旋、和湿式除尘方法在真空吸尘器中的比较外文翻译资料
• 一个灵活的模型辗环机设计外文翻译资料
• 带有柔性转子的主动电磁轴承系统的识别外文翻译资料
• 柔性阻尼支承下转子振动特性实验外文翻译资料
• MapReduce:超大集群上的数据简化处理外文翻译资料
• 垂直循环式立体车库的停车与乘车调度优化外文翻译资料
• 高灵敏度、高稳定性的自温度补偿电涡流位移传感器外文翻译资料