
英语原文共 6 页,剩余内容已隐藏,支付完成后下载完整资料
600Kgf型装卸机器人的结构分析
Gwang-Jo Chung1,Doo-Hyung Kim2
摘要:设计重型工业机器人操纵器,它必须进行测试和评估整体结构体。在根据运动学确定的部件配置和机器人结构的动力学分析后,进行测试和评估程序。在这项研究中,我们通过对每一种模拟进行了可行性研究,通过专门设计的组装部件确定详细的重型搬运机器人的数字和规格。第一,我们对600Kgf(最大)的重载和机器人的体重,完成了刚体动力学分析的模拟。结果,我们获得了每个关节可用于静态刚度分析的最大反作用力。接下来,通过模式分析,我们估计整体的固有频率并将其与实验结果进行比较去识别FEM的准确性和靠性模型。最后,我们分析了弹性 - 刚体动力学去估算零件在工作运动中机器人的稳健性。
关键词:重载,机器人,机械手,结构,分析,静态,动态,估计
一、引言
在重型行业如汽车,造船厂,机床行业中,机器人的作用是一个决定自动化水平的重要参数。 为了减少处理时间和成本,最小处理单位机器部件可能会更重,这可能需要一个机器人操纵器的有效载荷更高。 特别是在汽车行业,在这个重型机械手的帮助下可能会集成几个流程。 目前,出于这个原因,发达国家,如德国、英国和日本出现了几款重型搬运机器人高达1吨的有效载荷。为了同样的目的,我们开发了有效载荷600kgf的重型搬运机器人。基本结构和规格如下:
- 有效载荷量:最大600kg;
- 水平移动距离:2.5米;
- 重复精度: /- 0.4毫米或更小;
- 自由度数:6;
- 运动速度:J1〜J3轴:最大 80度/秒 ;J4,J5轴:最大 100度/秒;J6轴:最大160度/秒;
- 手腕力矩:J4,J5轴:Max 340 kgf.m;J6轴:最大170 kgf.m。
二、有限元件模型
图2显示了三维配置模型和有限元模型。有限元模型从每个链接部分的几何模型导出,基于在3D二十节点结构固体组件上由每个节点和三个自由度组成二十个节点构成模型的一个元素。要完成网格,需要168,758个节点和51,858个元素被指定如表I所示。表II和III显示了这些材料及其特性应该是均匀分布,0mass在有限元模型中用于静态和动态估计动态刚性。另外,我们采用的转关节是具有一个自由度的部件和圆柱形接头,用于两度的旋转和平移运动自由。为了减少第二轴电机的负载,在轴#1和高轴之间下臂(轴#2)t的位置我们使用了一个弹簧平衡单元,刚度为2.15N / mm左右。基于以上有限元模型,在对静态刚度评估和分析后,我们执行了刚体动力学分析,得到了在每个接合处产生的最大反作用力。
- 3D配置模型 (b) 有限元模型
图2.机器人结构的分析模型
表1. 节点数和元素数
|
E 模型 |
|
|
节点总数 |
168,758 |
|
元素总数 |
51,858 |
表2. 每部分的材料
|
部位名称 |
重量(kg) |
材料 |
|
底座 立柱 下臂 机动总装 操作杆 平衡重量 并行连接 框架总装 上臂总成 5轴壳体组件 6轴壳体组件 气缸组件 |
344 686 214 350 158 598 40 172 135 55 70 64 |
GC250 GCD450 GCD450 GCD450 GCD450 GC250 GCD450 GCD450 GCD450 GCD450 GCD450 STEEL |
|
Total |
2885.467(kg) |
表3. 机械特性
|
弹性系数 |
泊松比常量 |
屈服强度 |
拉伸强度 |
|
110 163 200 |
0.29 0.3 0.29 |
- 362 - |
252 420 460 |
三、刚体动力学分析
A、重型搬运机器人的建模
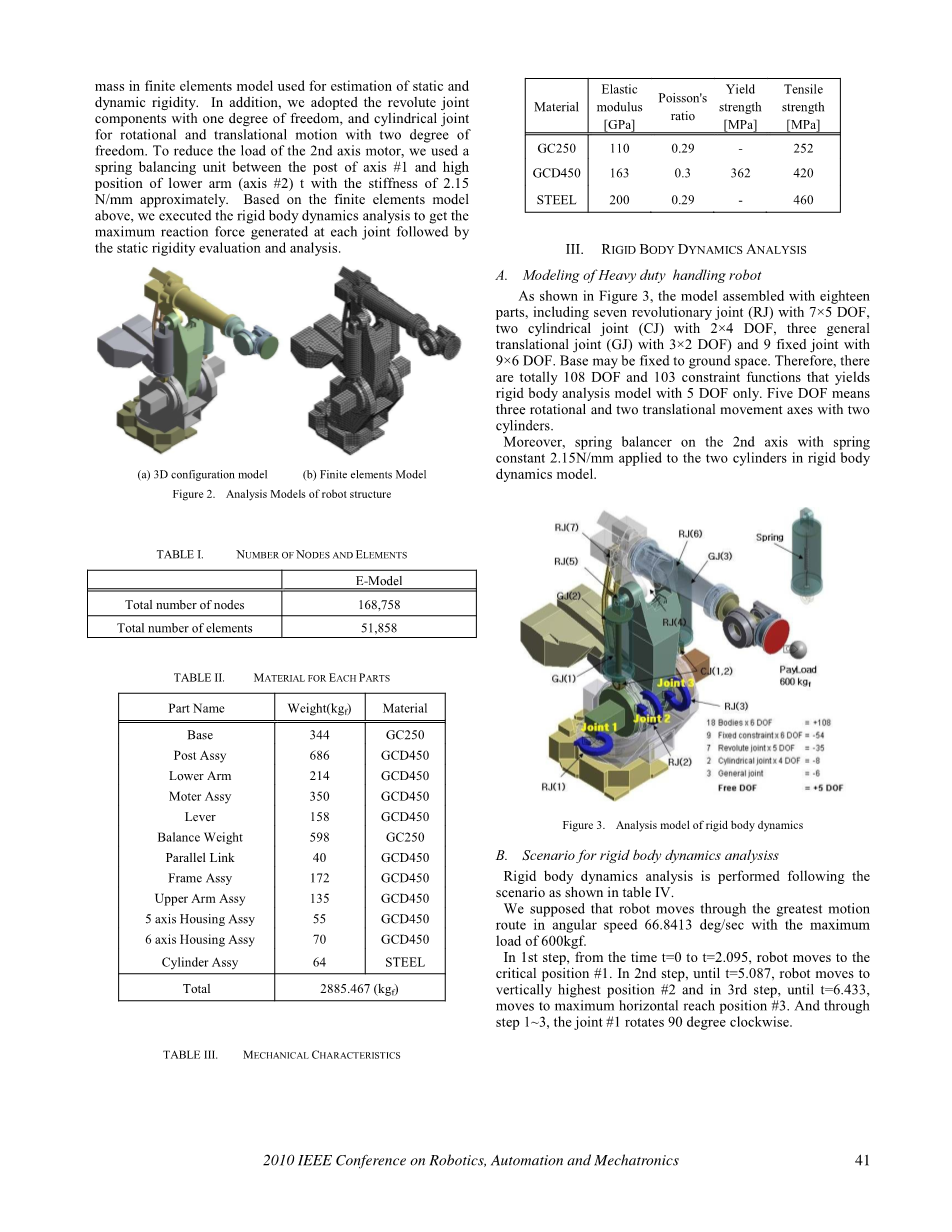
如图3所示,该模型与十八个部件组装在一起部件,包括7个革命性接头(RJ),7times;5自由度,两个圆柱形接头(CJ)用2times;4自由度,三个通用接头,具有3times;2自由度的平移连接(GJ))和9个固定连接,9times;6自由度。基座可能固定在地面上。因此,仅具有5自由度的刚体分析模型,就共有108个自由度和103个约束函数。 五个自由度意味着三个旋转轴和两个平移轴缸。
此外,第二轴上的弹簧平衡器带有弹簧恒定2.15N / mm应用于刚性体中的两个气缸动力学模型。
图3、刚体动力学分析模型
B、刚体动力学分析情景
刚刚进行的刚体动力 学分析是在下面进行的情景如表四所示。
我们认为机器人可以通过最大的动作是最大角速度66.8413度/秒负载600kg。
在第一步中,从时间t = 0到t = 2.095,机器人移动到关键位置#1。 在第2步,直到t = 5.087,机器人移动到垂直最高位置#2和第三步,直到t = 6.433,移动到最大水平位置#3。并通过步骤1〜3,关节#1顺时针旋转90度。
表4.机器人运动的场景
|
步数 |
时间 |
节点1 |
节点2 |
节点3 |
临界点 |
|
0 1 2 3 4 5 6 |
0 1.407 2.095 3.591 5.087 5.760 6.433 |
0 0.749 0 0.525 0 1.166 0 |
0 1.166 0 -1.166 0 -1.166 0 |
0 0.499 0 0 0 -1.166 0 |
- - 位置1 - 位置2 - 位置3 |
C、每个关节的反作用力
我们将所有的机器人部件描述为没有弹性,但有一个仅具有质量特性的刚体。通过固定身体动态分析情景,我们可以用作静态刚度分析的输入值推导出反应力。图4(a),(b),(c)显示出了机器人在位置#1,2的情况,表4中的情况见表3。
这些姿势代表了一些特殊的弱点,在平行连杆,下臂和肘关节动力学条件恶劣的情况下,我们采样动态加载数据记录的框架。图5(a)显示了反应力的历史并行链路和帧RJ(7),最大值为23,717N在5.087秒。
图5(b)显示了下臂之间的反作用力和框架RJ(4)在5.087秒时,力的最大值为33,048 N.。
图5(c),(d)显示了机架臂之间的反作用力和两个弹簧平衡器RJ(5)/ RJ(6),力的最大值为786.01 N和760.18 N每个发生在6.28秒。
- 2.1 秒 (b) 5.08秒
- 5.08秒
图4.机械手的姿势
图5.刚体动力学分析中的旋转关节记录
四、静态刚性分析
对于静态刚度分析,我们让边界条件和负载条件如图6所示。
边界条件是建立在底部底板和负载条件(机器人重量加上有效载荷600kg位于离中心位置261mm处的法兰)之上。
图7显示了在这些边界和负载条件下的正常姿势的静态偏转和应力分布。
为了估计静态刚度,我们已经确定了每个关节的最大反作用力。
图8(a)显示了将最大值动态负荷23.717 k N加载到并联连杆关节的分析结果。图8(b)也显示了通过把最大反作用力33.048 KN 加载到下臂和框架之间,并把反作用力786.01 N和760.18 N 加载到下臂和轻/左弹簧平衡器之间的应用分析结果。而图8(c)显示了应用33.048的分析结果框架和柱子之间的k N和23.717 k N之间帧和并行链接。情况(c)的结果产生84.632MPa的等效应力略高于另一方的估计值组件。 但是,收到的价值非常稳定材料GCD450的拉应力小于20%(420 MPa约)。
- 有效负载 重量 (b)底盘
图6. 静态刚度分析的边界和载荷条件
- 应力分布 (b)静态挠度
图7. 挠度和应力分析
- 平行连杆 (b)下臂
- 框架和上臂
图8.最大应力分布。 施加反作用力
五、动态刚度分析
A、模型分析
对于机器人的优化设计,它需要模式分析确定自然频率和自然模式。 模式分析的边界条件可能是与静态刚度评估相同。 但是,潜在的必须将皮重引起的压力视为图9显示皮重的偏转分布。
图10和表V显示了估计的自然值频率介于0 Hz至150 Hz之间。
估计第一模式下的固有频率为18.05赫兹,具有出色的平衡水平振动观察到的重量在第六模式下具有相同的外观。第二,第三和第四的自然频率日 &5th模式分布在19.95〜33.94 Hz带宽的对角线上振动。 在第七模式中,我们观察了平衡重量严重震动,并在更高的模式下链接组件开始扭曲。
所以自然频率在18.05〜35.19Hz之间被认为是有效的,主要针对机器人的运动结构如表五所示。表六显示了第一个固有频率的结果平行连杆,下臂,框架和上部的模态分析臂。 我们承认所有的第一固有频率是单个周期性组件。
图9.通过皮重分配挠度
B、弹性 - 刚性多体分析
条件下机器人振动的影响,必须考虑机器人结构的弹性效应估计。 为此,我们执行了弹性 - 刚性按照上述方案进行多体分析。为了减少时间和人力,我们应用了弹性模型在上臂,下臂,框架等几个部位,平行连杆和杠杆作为比较巨大的动态反应。 其他部分建模为僵化身体。 图11显示了每个关节的反作用力矢量弹性 - 刚性多体分析。
表五. 机器人结构的固有频率
|
设置 |
频率 [Hz] |
|
1 2 3 4 5 6 7 8 9 10 11 |
18.047 19.950 21.510 28.515 33.941 35.190 63.937 80.000 90.489 125.16 147.43 |
- 模式1(18.05Hz) (b)模式2(19.95Hz) (c)模式3(21.51Hz)
- 模式4(28.52Hz)(e)模式5(33.94Hz)(f)模式6(35.19Hz)
图10.每种模式下的频率
表六、机器人每部分结构的固
全文共6786字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[11711],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


