
英语原文共 6 页,剩余内容已隐藏,支付完成后下载完整资料
一种用于电磁波,声波和水波的超表面地毯披风
我们提出了一种不显眼表面下的地毯式披风,以在三种不同的波(即电磁波,声波和水波)下隐藏具有任意形状和大小的物体。我们首先介绍一个可以控制这三个波的局部反射相位的超表面。通过利用该超表面,我们设计了一个超表面地毯披风,该披风提供了额外的相位,以补偿由凸块引起的相位失真,从而恢复反射波,就好像入射波撞击到平面镜上一样。有限元模拟结果表明,可以用单个超表面披风将物体隐藏在这三种波下。
随着超材料的发展,在科学上可以实现隐形斗篷,这些隐形斗篷吸引了研究人员对电磁界的极大兴趣。有两种主要策略,即取消和转换光学已开发来设计隐形斗篷。在基于散射消除的方法中,电介质被等离子体材料覆盖。两个物体中的偶极子相互抵消,因此总散射将大大减少。可以用超薄人工层(即所谓的超表面)进一步替换体积等离子体激元披风壳第二种方法是变换光学,由Pendry和Leonhardt等人提出,通过利用麦克斯韦方程组的“度量不变性”,可以基于坐标变换在物理空间中创建“孔”。光线可以在隐藏的物体周围平稳地引导,并通过斗篷传播,而不会产生任何干扰。因为坐标变换是从点到线(圆柱隐身衣)或表面(球形隐身衣)并且隐身衣的参数包含极值,所以通常很难实现孤立的隐身衣。为了消除极端参数,提出了从虚拟空间中的一条线转换为物理空间中另一条线的地毯,以将物体隐藏在反射表面上。但是,上面介绍的所有毯子披风的厚度通常与隐藏物体的大小相当。为了克服这一挑战,最近,人们提出了几种表面隐身的斗篷。在超表面地毯的斗篷中,隐藏的物体被超薄梯度超表面覆盖,该超薄梯度超表面用于控制局部反射相位并恢复反射波。这些研究表明,超表面地毯披风可以在宽入射角和宽带宽范围内隐藏任意形状和大小的物体,但并没有引入横向位移作为传统的拟拱形测绘的电磁波散装斗篷。
作为电磁披风的类似物,声学披风也越来越受到关注,由于其潜在的应用。借助声学超材料,已经实现了一些声学隐身衣,包括基于散射消除的声学隐身衣,2D声波全向披风,2D隔音地毯披风和3D隔音地毯披风等等。注意,隐形斗篷的概念也已扩展到其他物理系统,例如线性液体表面波、地震波、热场、静磁场和电场、物质波等。
最近,已经进行了一些尝试来设计和实现多物理场披风。Moccia 和Li等在理论上证明,仅使用一种超材料结构就可以独立地控制直流电流场和热场。Ma等人进一步验证了该理论。这个事实背后的物理机制是热传导方程和电传导方程都是拉普拉斯方程。Xu等人还发现,以前引入的用于线性表面液波的圆柱形披风对于声波和电磁波同样有效。原因是二维铝制掩盖结构的数学模型(具有Neumann边界条件的Helmholtz方程设置为铝元素的边界)对横向电磁波(TM)有效(铝元素在微波中的行为就像是完美的电导体(PEC))。它也可以应用于声波(它们的行为类似于空气中的刚性夹杂物)和水波(如果铝元素高于水面,则没有流动条件)。
在本文中,我们将地表地毯的披风概念从电磁波扩展到了另外两种波,即声波和水波。我们提出了一种可以处理电磁波、声波和水波的单一多波地表地毯披风。在此,“多波超表面”是指一个多种波表面适用于多种波。用单个披风操纵三个波的物理机制是,超表面披风的相同数学模型可以适用于电磁波、声波和水波。在以下各节中,我们首先介绍超表面隐身衣的基本原理,然后演示三种波的隐身性能。我们的模拟结果表明,一个单一的超表面地毯披风可以成功隐藏这三个波浪下的物体。
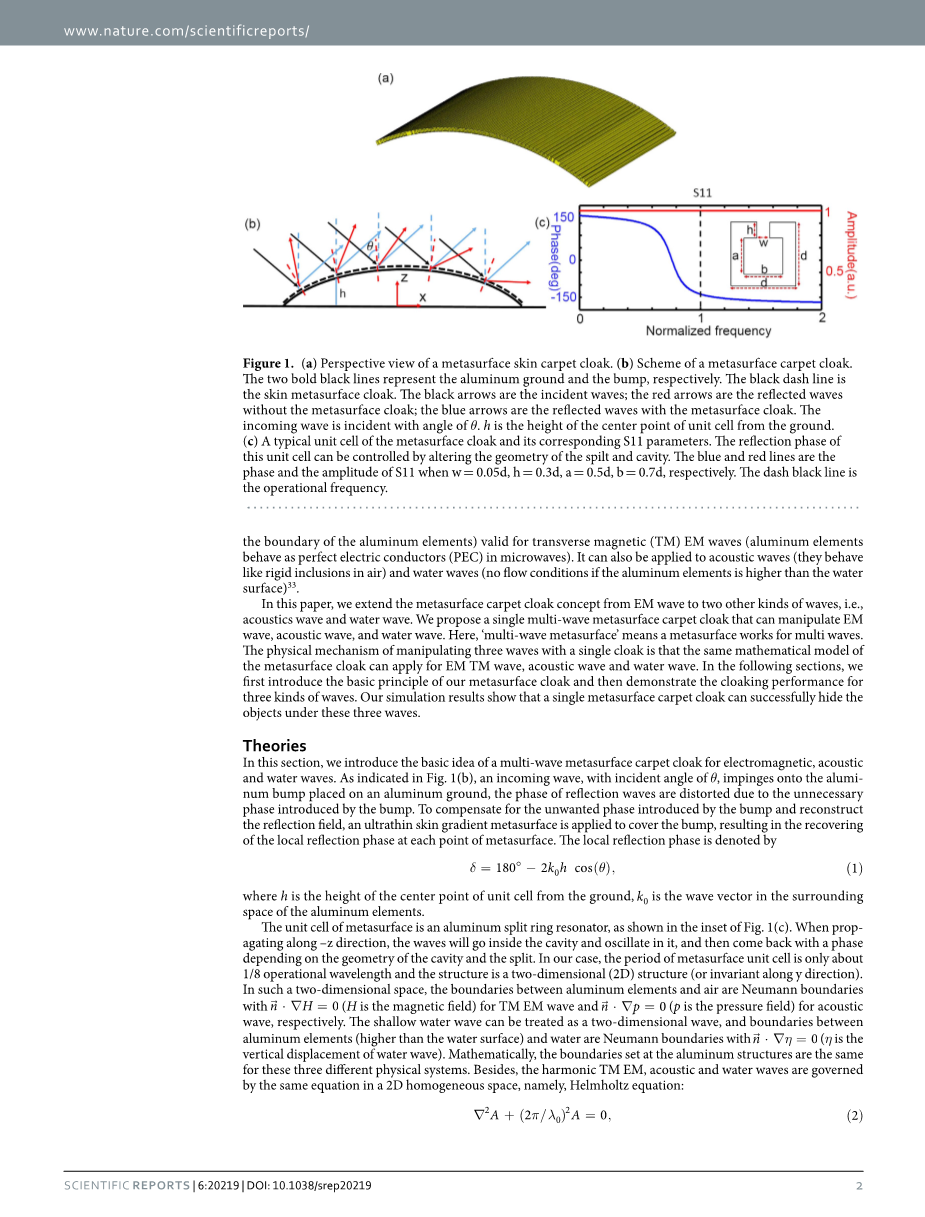
图1.(a)超表面地毯披风的透视图。(b)地表地毯披风的方案,黑色的两条粗线分别表示铝制接地线和凸起,黑色虚线是皮肤表面隐身披风。黑色箭头是入射波;红色箭头是没有超表面隐身的反射波。蓝色箭头是带有隐身披风的反射波。入射波以theta;角入射。h是单位单元距地面的中心点的高度。(c)地表披风的典型晶胞及其相应的S11参数。该晶胞的反射阶段可以通过改变溢出物和空腔的几何形状来控制。蓝线和红线分别是当w = 0.05d,h = 0.3d,a = 0.5d,b = 0.7d时S11的相位和幅度。黑色虚线是工作频率。
理论
在本节中,我们将介绍用于电磁波、声波和水波的多种波超表面地毯披风的基本概念。如图1(b)所示,入射角为theta;的入射波撞击到放在铝制地面上的铝制凸块上,由于凸块引入了不必要的相位,反射波的相位失真了。为了补偿由凸块引入的不想要的相位并重建反射场,应用超薄皮肤渐变形超表面来覆盖凸块,从而在形变表面的每个点处恢复局部反射相位。局部反射阶段用公式(1)
delta;= 180°-2k0h cos(theta;), (1)
其中h是单位晶胞距地面的高度,k0是铝元素周围空间中的矢量。
超表面的晶胞是一个铝制裂环谐振器,如图1(c)所示。沿–z方向传播时,波将进入空腔内部并在其中振荡,然后根据空腔的几何形状和裂口返回一个相位。在我们的情况下,超表面晶胞的周期仅约为1/8工作波长,并且该结构是二维(2D)结构(或沿y方向不变)。在这样的二维空间中,铝元素与空气之间的边界是诺伊曼边界,对于电磁波,nsdot;nabla;H= 0(H是磁场),nsdot;nabla;p = 0(p是压力场)分别用于声波。浅水波可以看作是二维波,铝元素(高于水表面)和水之间的边界是Neumann边界,nsdot;nabla;eta;= 0(eta;是水波的垂直位移)。在数学上,这三个不同的物理系统在铝结构处设置的边界是相同的。此外,电磁波、声波和水波在2D均匀空间中由同一方程式控制,即Helmholtz方程式:
nabla;2A (2pi;/lambda;0)2A = 0, (2)
对于电磁波,其中A = H;A = p,对于声波和 水波,A =eta;,并且lambda;0是均质材料中的波长。因此,我们在三个不同物理系统中的晶胞的数学模型是相同的,即在铝结构上设置了Neumann边界条件的Helmholtz方程。作为Equ中的A(2)仅与波长有关。因此,如果这三个波的波长相同,则场分布将完全相同。我们在下面显示了典型单位晶格的S11参数图1(c),其中w = 0.05d,h = 0.3d,a = 0.5d,b = 0.7d(d是单位晶胞的周期)。水平轴是归一化的频率,f= 8d /lambda;0,垂直轴是S11参数。
图2.(a)当声平面波垂直入射到隐蔽的凸块上时的压力场分布。(b)当平面水波垂直入射到隐蔽的凹凸物上时,水面的垂直位移。(c–e)当EM平面波分别垂直入射到隐蔽的凸块、平坦的地面和裸露的凸块上时的磁场分布。(f)每个亚波长段的局部反射相位。
模拟
在本节中,我们设计具有几种不同入射角的两种形状的超表面披风,以证明我们的方案适用于任意形状。在第一个示例中,我们模拟了入射角为0°的弧形超表面披风,而在第二个示例中,我们对了入射角为45°的三角形披风进行了建模。我们的弧形斗篷中的弧形曲线描述为:
其中R是圆弧曲线的半径。因此,局部反射阶段为
delta; = 180 minus; 2k0z. (4)
在我们的设置中,R等于57.3d,且超表面隐身衣由60个晶胞组成。每个晶胞的局部反射相位如图2(f)表中显示了每个晶胞的大小,补充信息中的S1。我们使用商业有限元软件包COMSOL MULTIPHYSICS对超表面披风进行建模。在模拟中,d = 7.5 mm,源是沿–z方向传播的平面波,在模拟域的所有侧面均应用了完全匹配的层(PML)以减少散射,并将所有边界设置为散射边界。图2(a–c)分别显示了在声波、水波和电磁波的隐蔽凸块附近的场分布,工作波长为60 mm。为简便起见,我们仅在电磁波照亮平面和裸露的凹凸时显示场模式,如图2(d,e)所示,根据之前的分析,声波和水波情况与电磁波相同。显然,当平面波撞击到裸露的凸块上时,反射波阵面将失真,如图2(e)。我们的超表面披风可以提供额外的相位,以补偿由凸块的几何变形引起的相差,从而强烈抑制了凸块的散射。对于声波电磁波和水波这三种波,重构后的反射波的相位和振幅几乎是完美的如图2(a–c)。
尽管此超表面披风是为0°入射角设计的,但它也可以在其他入射角上工作。我们模拟了几种不同的入射角,以证明我们的超表面披风的操作视角。当入射角为10°时,隐形凸块,接地凸块和裸露凸块的相应磁场分布如图3(a–c)所示,为简单起见,这里我们仅显示电磁波动情况。由于入射波将与反射波重叠,因此沿z方向的波为驻波,如图3(b)所示。比较图3(a)在(c)中,很明显,隐身披风表现出良好的隐身性能。图3(d–f)可见操作视角可以扩展到20°,这意味着我们的斗篷至少可以在-20°至20°的视角范围内工作。
图3.(a–c)入射的EM平面波以10°入射角分别照射隐蔽的凸块,地面和裸露的凸块时的磁场分布。(d–f)当入射的EM平面波以20°入射角分别照射隐蔽的凸块,地面和裸露的凸块时的磁场分布。
图4.(a)当高斯声束从左上角以45°的入射角入射到隐蔽的凸块上时的压力场分布。(b)当水高斯光束从左上角以45°入射角入射到隐蔽的凸块上时的垂直位移分布。(c–e)当EM高斯光束从左上角分别以45°入射角入射到隐蔽的凸块、地面和裸露的凸块上时的磁场分布。(f)每个亚波长段的局部反射相位。(g)沿(c,d)中标记的黑线的局部相位,其中水平轴是从左端点到黑线的长度。
在第二个示例中,我们为入射角为45°的高斯光束设计了一个三角形的超表面地毯披风。三角形凹凸的轮廓表示为:
z=-0.33| x| 12d(-36d<x<36d) (5)
因此,局部反射阶段为
delta;= 180-2k0z cos(45) (6)
每个晶胞的局部反射相位如图4(f),表中显示了每个晶胞的大小。S2中的补充信息。在仿真中,波源是从左上角以45°入射角入射的高斯光束。三种不同波的场分布结果相同,为简单起见,我们仅显示裸露的凸块和接地情况的电磁波结果。正如预期的那样,只有裸露的铝凸块反射波会失真,并且在凸块后面会形成一个大阴影,如图4(e)所示。用梯度超薄形超表面覆盖凸点后,将恢复变形的反射波,包括电磁波、声波和水波,并保留高斯光束轮廓,如图4(a–c)所示。为了更清晰比较,我们显示图4(f)沿黑线标记的磁场相位图4(c,d)。显然,隐蔽的凸起的场相线与平面镜的场相线非常匹配。此外,有趣的是,我们的方法消除了准保形映射方法不可避免的横向偏移。我们还显示了入射角为37.5°和30°时的场分布。用于电磁波仿真结果图5结果表明,这种基于超表面的披风在30°至45°的入射角范围内都能很好地工作。
结论
总而言之,我们提出了一种不显眼的地毯超表面披风,用于在电磁波、声波和水波下隐藏任意形状和大小的物体。单个超表面可以控制这三种不同波的局部反射相位。通过利用这种超表面,我们设计了一种多波超表面地毯披风,该披风可以提供额外的相位,以补偿由凸块引起的相位失真,从而恢复反射波并保留波前形状,就像入射波一样。撞击在平面镜上。有限元模拟表明,我们可以用一个超表面的披风将物体隐藏在三个不同的波浪下。第一个披风的容许入射角至少为-20°至20°,第二个披风的角度为30°至45°。此外,这种超表面披风没有反射光束的横向偏移。
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[237683],资料为PDF文档或Word文档,PDF文档可免费转换为Word


