
英语原文共 13 页,剩余内容已隐藏,支付完成后下载完整资料
提高低负载下三相PWM逆变器转换效率的三相交流滤波电感器设计
摘要:
本文评估了三相脉宽调制(PWM)逆变器中使用的三相交流滤波电感器中的电感器损耗。首先,设计了一个三相电感器,以使每个相的电感值相同。然后,基于该设计,提出了一种使用两种磁性材料的三相电感器。模拟了使用传统和本文提出的两种交流滤波电感的1 kVA三相PWM逆变器的转换效率。仿真结果表明,转换效率有所提高。最后,测量了建议下的交流滤波电感器的实际三相1 kVA PWM逆变器的转换效率和传统的相对比。在实验中,与常规电感器相比,在低功率负载下针对提出的电感器的情况获得的转换效率提高了约1%。此外,计算出的电感器损耗与测得的损耗非常一致。通过模拟和实验验证了效率的提高。
1.简介
随着信息和通信系统中功耗的急剧增加,提高信息和通信电源的效率已成为迫在眉睫的问题。 数据中心和其他设施中使用的不间断电源(UPS)和电源单元(PSU)具有冗余配置,以提供电源系统所需的可靠性,这导致正常情况下的低负载运行。 因此,不仅在额定输出时还需要高效率,在低输出时也需要。
由于使用了碳化硅,氮化镓和其他在最近几年迅速普及的组件,功率器件的损耗已大大降低。另一方面,由于 高频开关;然而,在这些设备中,基于定量损耗分析的损耗降低技术尚未得到充分发展。因此,关于温度上升以及低输出和额定输出时的效率的变压器和逆变器的设计仍然很困难。
在用于互连的三相脉冲宽度调制(PWM)逆变器中,功率器件的损耗随着输出功率的减小而减小,但交流滤波电感器的铁损几乎保持不变,而与输出功率无关。 已经反映出了减少交流滤波电感器铁损对于提高低负载效率的重要性。
在本研究中,我们考虑了一种用于三相PWM逆变器的在具有EE磁芯的三相交流滤波电感器中准确损耗计算的方法,并将该方法应用于新的电感器设计以提高低输出时的电感器效率。首先,我们进行磁路分析,以推导三相逆变器中带有EE磁芯的三相电感器的设计与各相电抗之间的关系。然后,我们研究了在使用单一磁性材料(铁粉)的情况下三相感应器各磁路的磁通密度特性,并介绍了使用两种磁性材料(铁粉和铝硅铁粉)的三相感应器的新设计,以减少损失。此后,我们计算使用传统三相电感器和建议的电感器的1 kVA三相逆变器的电感器和半导体器件的损耗,并估算由于在三相PWM逆变器中采用建议的电感器而带来的效率改善效果。最后,我们测量了两种类型的电感器和1 kVA三相PWM逆变器中的损耗,以证明所提出的电感器可提高低输出时的逆变器效率。
2.三相PWM逆变器中励磁的三相电感的设计
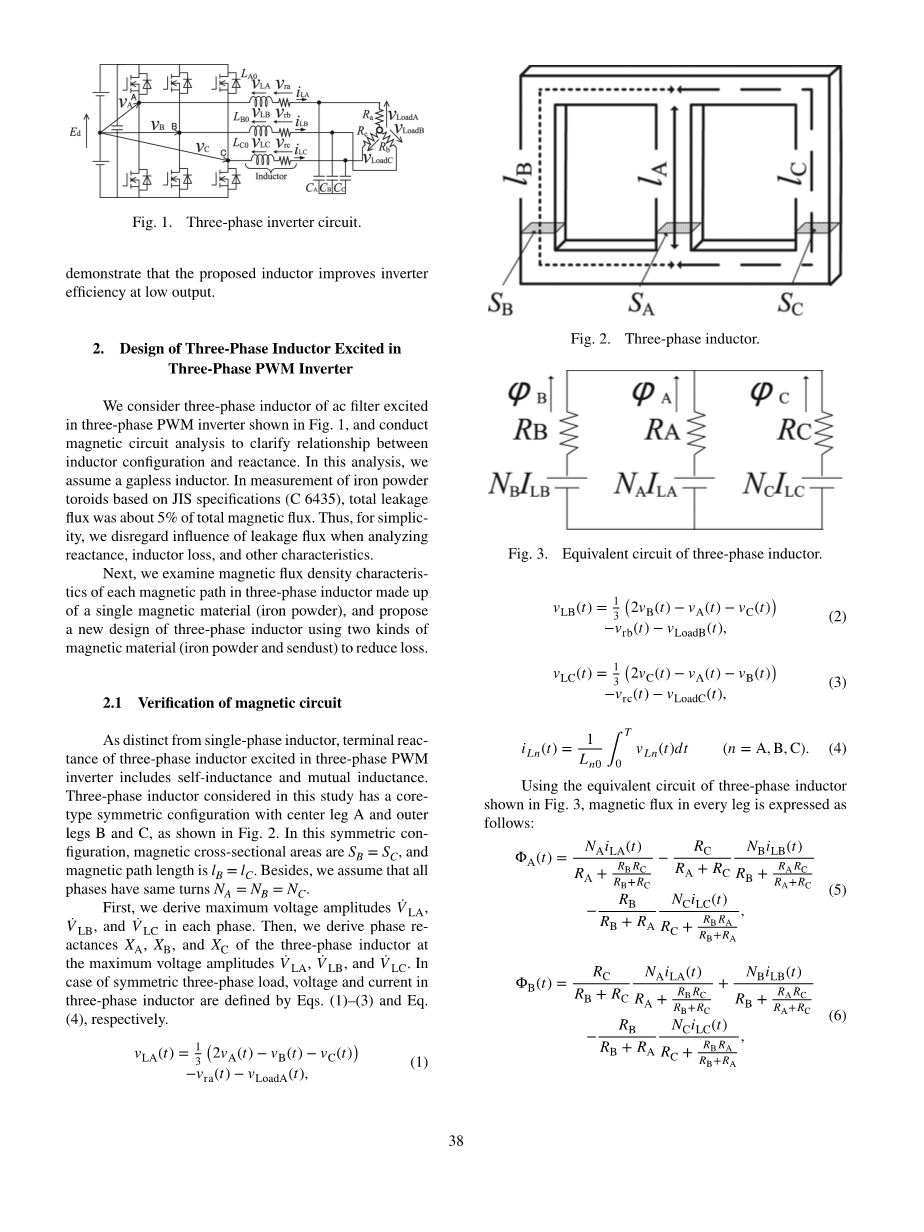
我们认为交流滤波器的三相电感在三相PWM逆变器中励磁如图1,并进行磁路分析以阐明电感器配置与电抗之间的关系。在此分析中,我们假设使用无间隙电感器。在基于JIS规格(C 6435)的铁粉环形线圈的测量中,总漏磁通约为总磁通的5%。因此,为简单起见,在分析电抗、电感损耗和其他特性时,我们忽略了漏磁通的影响。
图1 三相逆变器电路
接下来,我们研究由单一磁性材料(铁粉)组成的三相电感器中每个磁路的磁通密度特性,并提出一种使用两种磁性材料(铁粉和铝硅铁粉)的三相电感器的新设计以减少损失。
2.1磁路验证
与单相电感不同,在三相PWM逆变器中励磁的三相电感的端电抗包括自感和互感。如图2所示,本研究中考虑的三相电感器具有芯型对称配置,中心支路A和外部支路B和C。在这种对称配置中,磁横截面积为SB = SC,而磁横截面积为 路径长度为lB = lC。此外,我们假设所有相具有相同的匝数NA = NB = NC。
首先,我们得出每个阶段都包含的最大电压幅度LA、LB和LC。然后,我们得出最大电压幅度LA、LB和LC的三相电感器的相抗XA,XB和XC。对于对称的三相负载,三相感应器中的电压和电流分别由公式1-3和公式4。
(1)
(2)
(3)
(4)
使用图3所示的三相电感器的等效电路,每条臂中的磁通量表示如下:
(5)
(6)
(7)
图3三相电感器的等效电路
在此,,,。
假设通量链接(通量乘以圈数)为phi;A=NAPhi;A,phi;B=NBPhi;B,并且phi;C=NCPhi;C,则可得到以下表达式:
(8)
考虑到互感的对称性,公式8可以等效为公式9。
(9)
通过用LA,LB和LC表示的三相电感器的自感以及用MAB,MBC和MCA表示的互感器,可以使用电感器电流iLA(t),iLB(t)和iLC(t),如公式10-12所示。
(10)
(11)
(12)
公式9至12是电感电压和电流的基本公式,对电流没有任何限制。 在本研究中,我们考虑一个三相三线逆变器。因此,我们对三相配置中的电流施加约束,如公式13所示。此外,假设对于侧边电阻,RB = RC = R,对于线圈匝数,NA = NB = NC = N,则等式10-12可以改写为等式14-16。
(13)
(14)
(15)
(16)
接下来,我们得出电感器每相中的最大电压幅度LA、LB和LC。假设相电流为iLA(t)= ILcos(omega;t),iLB(t)= ILcos(omega;t–2pi;/3),iLC(t)= ILcos(omega;t 2pi;/3),则最大电压幅度LA、LB和LC得到分别为omega;t= 0,omega;t=2pi;/3和omega;t= –2pi;/ 3。因此,可以得出以下内容:
(17)
(18)
(19)
可从最大电压幅度LA、LB和LC中找到三相感应器各相的电抗XA,XB和XC和电感器电流幅度IL,如公式20-22。
(20)
(21)
(22)
在使用EE形磁芯的商用三相逆变器中,所有横截面面积通常等于10;但是,在横截面和匝数相等的情况下,中支脚的磁阻与侧支脚的磁阻不同,即RA = R不成立。
假设电抗的XB = XC = X,则与XA的差Delta;X可以表示为:
(23)
此外,XA和XB(或XC)之间的相对差sigma;可以写为:
(24)
三相转换器中使用的滤波电感的电抗X是针对负载阻抗设计的,以避免电感上的电压降。
在本研究中,如下所述,将电感器的%X设置为2.4%,对于图5中的常规电感器配置,中心臂的磁阻为RA = 0.54R。在这种情况下,XA和XB(或XC)之间会出现约7.7%的相对差,而A相和B相(或C相)之间会出现约0.18%的输出电压的相对差。但是,可以认为中脚的磁阻RA和侧脚的R之间的差异对三相电流不平衡的影响很小。
因此,设计三相电感器,在随后的讨论中参考公式20至22。这样,我们可以通过修改三相电感的配置并根据每个磁路中激发的磁通密度B来选择磁性材料,从而降低三相电感的铁损。
各种磁性材料的饱和磁通密度与相对磁导率mu;i之间的关系如图4所示。从图中可以看出,相对磁导率mu;i随着较低的饱和磁通密度而增长。
图4磁性材料的特性
关于对钴基非晶合金,铁硅铝粉,铁粉和其他磁性材料的评估,据研究结果说明,铁磁损耗随着饱和磁通密度11、12的增加而降低。因此,如果选择适当的磁性材料,则可以降低铁损耗,达到电感脚中激发的最大磁通密度。
2.2根据电感的励磁特性选择磁性材料
假设图1中的三相三线PWM逆变器,我们为1 kVA的逆变器输出设计了交流滤波电感器。表1给出了1 kVA三相逆变器的规格。%X设置为2.4 p.u.时,我们设计电感器,使其在最大负载下的电流纹波相对于基波为20%。此外,我们假设逆变器输出Pout 可以在221 W至835 W的范围内变化。在随后的有关铁损评估的讨论中,将835 W的输出定义为1 p.u的正常运行。
首先,我们考虑使用单一磁性材料(铁粉)制成的三相电感器,如图5所示。与典型的商用三相电感器一样,此处所有横截面的设计均相等。
图5常规三相电感器
接下来,我们考虑三相感应器中每条腿的磁通密度特性,并检查使用多种磁性材料(铁粉和铁硅铝粉)的三相感应器。如图4所示,铁损比铁粉低。此外,铁粉的饱和磁通密度比铁粉13低约30%。因此,仅由铁硅铝制成的三相电感器将比由铁粉制成的三相电感器大。
在本文中,我们提出了一种结构,其中可以使用多种磁性材料(铁粉和铁硅铝粉),如图6所示;具体而言,与传统设计相比,中心腿的横截面积SA减小了,从而可以调节每条腿中激发的磁通密度B。在建议的配置中,中心支脚的磁阻为RA = 0.77R;因此,与传统设计相比,电抗XA和XB(或XC)之间的差Delta;X减小,并且XA和XB之间的相对差sigma;从7.7%提高到3.9%。
图6本文提出的三相电感器
现在,我们来说明调整每条腿所激发的磁通密度B的原理。电感器中激发的磁通密度B由电感器电压vL,匝数N和横截面积S决定,如下所示。
(25)
在图2所示的三相电感器中,中心脚的磁阻RA随横截面积SA的减小而增大;因此,必须增加匝数N才能从等式中获得相同的电感%X。如图23和24所示。使用电路模拟器(PSIM)计算在磁脚中激发的磁通密度,表明中脚的磁通密度BA增大,而外脚的磁通密度BB,BC减小,如图7所示。因此,不同中心支脚和外部支脚可以获得最大的磁通密度值。如果三相感应器使用铁粉和铁粉,则两种材料之间的最大饱和磁通密度差约为30%。因此,调整中心腿的横截面积SA,以使中心腿的通量密度BA与外部腿的BB之间的差变为30%。也就是说,利用图6中提出的三相感应,可以用低损耗材料制成某些支脚,与由单一磁性材料制成的传统三相电感相比,有望降低损耗。
图7模拟的通量密度波形
本文设计了具有相同尺寸和电抗的电感器。另一方面,比较电感器工作时的最大容量非常接近但不相等。具体而言,建议的电感器的最大容量为27.4 VA,而常规电感器的最大容量为31.7 VA。此外,在所提出的电感器中,铜线的长度在中心脚中比在侧脚中小,因此绕组电阻较低。然而,电感器的%X被设计为2.4p.u.,并且,由于中心脚和侧脚之间的绕组电阻的差异而引起的%X的变化率为1.3%。因此,%X的变化小至0.03p.u.,绕组电阻的差异对电流不平衡的影响很小。关于铁损,建议的电感器和常规电感器都具有EE磁芯,并且铁损在中支脚和侧支脚中有所不同。额定运行中铁损为1 p.u.定义为PFe = RacI2L_RMS,根据铁损PFe和电感器电流的有效值IL_RMS计算得出的降低的电阻Rac,对于传统电感器的中臂为0.22Omega;,对于侧臂为0.46Omega;。另一方面,所建议的电感器的减小的电阻Rac对于中脚为0.24Omega;,对于侧脚为0.05Omega;。额定工作电压为1 p.u时的输出电阻。为34Omega;,并且在额定工作状态下,由于中心支腿和侧支腿之间的铁损而引起的铁损相对于负载的差异小于0.8%;因此,两腿之间铁损的差异对电流不平衡的影响也很小。
3.使用三相电感器验证三相PWM逆变器的效率改善效果
在使用常规三相电感器和建议的电感器的情况下,我们按照表1的规格计算图1中的三相逆变器的效率,并进行仿真以验证所建议的电感器是否有助于低负载运行中的逆变器效率 。 三相逆变器的效率eta;由逆变器电源引脚,三相电感的总损耗PInductor和半导体器件损耗PDevice计算得出,如式26所示。
(26)
3.1计算总电感损耗
三相电感器的总损耗PInductor是由于线圈中的焦耳损耗和铁心中的铁损耗PFe引起的铜损耗PCu之和。
假设图1中为三相逆变器的正弦输出,其工作波形如图8所示。在A,B和C相中使用调制信号vcA,vcB和vcC时,A相中的励磁电压vL如图8所示,滤波器电感是矩形波和正弦波叠加。同时,励磁电流iL,磁通密度B和磁场强度H是具有叠加纹波的正弦波。当在B‐H平面上显示磁通密度B和磁场强度H时,如图9所示,有一个与输出电流的50Hz基本成分有关的主回路和与开关纹波成分有关的次要回路。研究中,将与输出电流iL(LF)的50Hz基本成分相关的主回路定义为低频铁损PLF,将与半导体开关引起的电流纹波成分iL(HF)相关的次要回路定义为高高频铁损PHF。三相逆变器激励的三相感应器的铁损PFe为低频铁损PLF与高频铁损PHF之和。因此,三相电感的总损耗PInductor如式27所示。
(27)
图8三相PWM逆变器电路的工作波形
图9BH波形
这里,铁损PFe,低频铁损PLF和高频铁损PHF包括磁滞损耗,涡流损耗和过剩损耗。
3.1.1铜损的计算
铜损PCu由使用绕组电阻Rwire和电感器的有效电流IL_RMS计算,如公式28。至于铜线的集肤效应,我们忽略了它,因为在20 kHz的开关频率下集肤深度为0.46 mm。为了简单起见,我们也忽略了邻近效应。
(28)
此处,rho;是绕组电阻率,Swire是绕组截面积,lturn是绕组平均匝长。
通过式28可以从表1所示的三相逆变器的最大负载到低负载,从建议的电感和常规电感计算出铜损PCu。
因此,铜损PCu的计算结果如图10所示。因此,铜损PCu略有增加。此外,从公式28可以看出,PCu随电感有效电流的平方而变化。也就是说,PCu与输出功率成正比。
图10铜损计算
3.1.2低频铁损的计算
在这里,我们考虑低频铁损PLF的计算。由于激励分量是正弦波,因此可以使用传统上用于计算铁损的公式29式的Steinmetz方程来计算低频铁损PLF。
(29)
这里,Ve是电感
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[235314],资料为PDF文档或Word文档,PDF文档可免费转换为Word


