轨道轮在滚动过程中的热应力分析外文翻译资料

英语原文共 8 页，剩余内容已隐藏，支付完成后下载完整资料

轨道轮在滚动过程中的热应力分析

摘要：本研究的目的在于通过建立瞬态的热弹塑的有限元分析，模拟制动过程中产生的热量对轮和轨道之间的热应力的影响。在车轮旋转一次时，会因为由局部温升和温度改变所产生的热膨胀从而产生应力。我们的实验结果表明，由于温升和温度变化所产生的，会在表面以下0.1-0.5mm处的螺纹上产生相当大的局部应力。[DOI: 10.1115/1.4027544]

关键词：温升，热弹塑性有限元分析，轮轨有滑滚，运动，制动过程，微热开裂动。

1. 简介

在采用盘式制动器的有轨车辆在高密度的制动过程中，车轮踏面在不正确的解除条件下会在轨道表面发生较大的滑动现象虽然宏观上的滑动收到了限制，但是车轮防滑保护系统（WSP）并没有消除宏观

上的滑动现象。因为宏观滑移问题的产生，考虑到在接触区所接触的两个部件之间瞬间产生相当巨大的热量，就有可能导致沿着轮[1]表面产生细微裂纹。

本文通过不同方式阐述了轮子表面和内部热量的产生。Handa和Morimoto[1]通过实验和相对简单的2D热弹塑性有限元分析研究了这种情况，同时还考虑到了制动块系统运行过程中产生的热量。通过磁粉测试所产生的图像清晰地表明，由于高温（制动所产生）和轮轨连接中的牵引力（图1），在表面下方0.1-0.5mm处存在裂缝。

Peng等人[2]。使用更为复杂的非线性三维有限元模型研究了这种现象。不仅如此，他们还从制动块滑动引起的发热方面入手解决了这个问题，同时考虑到与冷轨接触的冷却影响，即所谓的“轨道冷却”效应。Wu等人[3]。使用热弹塑性2D有限元模型从轨道侧证明了轨道表面下方的特定拉伸变形和应力分布，可能导致微裂纹，这是由于滑轨通过轨道的检测点传递而引起的。在另一个出版物中，Handa等人[4]，通过测试装置显示并研究了裂缝形成和延伸的条件。他们通过实验确定，最初在胎面下方的区域中由塑性变形和热应力产生相当大的压应力，在冷却后转换成残余拉应力。从长远来看，这个过程可能会因其循环特征而导致破裂。参考文献[5]，考虑到热分区，开发了一种3D热弹塑性接触模型。该模型用于模拟半空间在静止球体上的滑动接触。讨论了压力，温度，地下应力和应变状态的结果。 Knothe和Liebelt [6]利用解析公式分析了实际轮轨连接时接触表面的热分布，他们研究了在计算方法中采用简化的衡热分布而非抛物线分布的差异。Ertz和Knothe[7]用解析和数值方法分析了车轮和钢轨之间的温度分布。在著名的Blok[8]公式的帮助下，他们确定了接触原件之间的最大接触温度。在Spiryagin等人的研究[9]中，建立了一个数学模型来评估非滑动和滑动条件下产生的表面温度。Kennedy等人使用FE模型对钢轨和车轮之间的温度分布和热分配进行了评价。他们解答了许多理论“在某些情况下可能产生不太符合现实的结果”的问题，因此，在目前的情况下，它不能用来评估在高佩特莱克数范围内所接触的现象的温度分布。

与上述作者相反，Sundh和Olofesson[11]通过测量分析了接触现象之间的热现象。采用针盘测量法对轮轨和轮缘钢轨连接处进行了分析。结果表明了分析区域内的温度最大上升过程并利用扫描电镜（SEM）分析了不同滑动速度下接触表面的微观和纳米结构的变化以及磨损情况。Gallardo-Hernandez等人烟柳了不同的磨损区域和轮轨机构，在两种五一平均接触温度相同的基础上，他们为两种机构建立了接触温度发展的分析热模型。

本文一方面通过实验——一方面主要是采用有限元分析法，给出了车轮踏面发热产生裂纹的发展条件；另一方面其中重点是通过制动块的摩擦产生热量。不得不说，上述现象同样也出现在装有盘式制动器的高速汽车上。其原因是中东后车轮在轨道上由于接触条件不理想而造成轻微滑动；其结果是，大量热的产生取决于速度的滑动和由于热膨胀产生的热应力。

本文利用ANSYS WORKBENCH V14.5 建立的有限元模型，对车轮踏面上下温度变化引起的热应力进行分析评估，分析了温度变化对车轮踏面损伤的影响。

图1. 车轮横截面表面裂缝

图2. 几何模型（两侧对称）

图3. 分段模型（竖直方向展开）

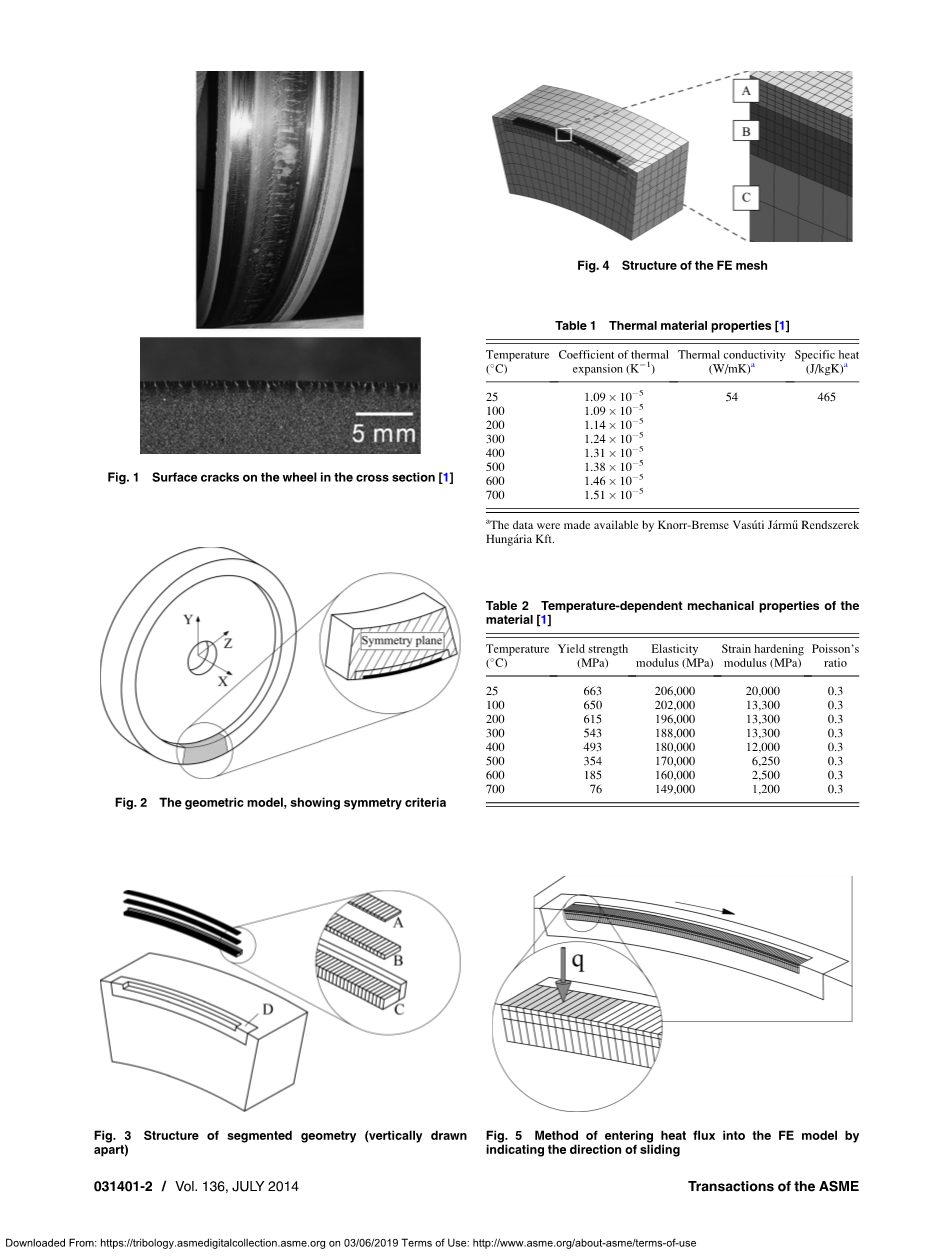
图4. 有限元网格结构

表1. 热材料特性[1]

a数据由 Knorr-Bremse Vasuti Jarmu Rendszerek Hungaria Kft.制作

表2. 与材料温度相关的机械性能 [1]

图5. 通过如图所指方向将热通量输入有限元模型

图6. 用于评估所测试的模型结果的查询路线的位置，st是沿滑动方向，Sd是沿深度方向。

1. 结构模型的体系结构

在我们的调查过程中，调查了一块14°直径为D=920mm[13]的轨道轮和简化的几何结构。在计算过程中，忽略了法兰盘和圆锥的形状。针对所建立出的几何结构模型在Y-Z平面完全对称，我们从所提取的切片中提取出半个模型进行计算

图2所示的分析段被细分为一个个的子段。这是为了在需要的地方产生足够精细的网格。细分为子段的另一个目的是为了使得移动热源的控制成为可能。如图3所示。

热负荷（A-B-C）影响较小的测试环境由120个较小的独立子段组成

为了简化链接，减少构件数量，在每个段之间产生一个所谓的有界网格[14]它定义了各个网格段之间的有界接触关系（图四）

为了提高计算精度，每一个分段采用20节点的六面体单元。基础体（图3在D之外的部分）的单元尺寸为10mm；D的标记端为5mm；用C标记的线段长为1mm；B段和A段的单元尺寸在切向减小到0.4mm，A段在沿深度方向上进一步细分为5个单元；因此，这里的单元高度为0.1mm。因此，有限元网格由37,108个单元和178,311个节点组成。

2.1. 分析所用材料性质。

在分析过程中，采用了与温度有关和与温度无关的热工材料性能(表1)和与材料温度有关的机械材料性能(表2)。在计算中应用了双线性运动硬化[14]材料定律。

2.2．边界和加载条件。

在计算过程中，以一辆运行速度为100km/h的车辆为基础，其车轮因制动沿轨道滑动。车轮的滚动速度是85km/h,代表了Delta;v=15 km / h的速度差,所以在车轮和轨道之间存在有约15%的滑动。在计算的过程中,车辆的总重量约为520 kN[13],代表每轮F=63750 n的负荷,假设汽车有四个轴。摩擦系数被认为是常数,值为mu;=0.15 [15]。初始温度是Tref=22℃。

在研究过程中，为了使有限元离散化更简单，将椭圆接触面积考虑为矩形。实际接触椭圆的一半宽度约为5mm，滑动方向的一半长度约为6.3mm;这些值以前是由有限元接触模型确定的[16,17]。为计算热源面积，用128.25mm的矩形面代替接触面积，假设接触压力为常数时，沿128.25mm的矩形表面的合力应与12.610mm的接触椭圆的情况相同(这种替代简化了热通量的计算说明)。如果热流分布是呈椭球形或恒定的，其计算出的接触温度只相差几个百分点[6]。

图7 特定时刻热源的移动情况，对应位置和时间日期(高亮的s坐标表示当前位置的中心和查询路线Sd的位置)；

图8 第一次旋转时模型区域的最高温升(见图2)

图9 t4时刻(第一次公转)沿查询行St的温度分布。带虚线的灰色背景表示接触区域的瞬时位置(见图7中的t4)。

图10 (a)查询路径St与Sd交点温度随时间的函数下降(第一次旋转)，(b)查询路径St与Sd交点温度随时间的函数下降(五转)

沿铁轨产生的热能滑动:

Q=mu;·Delta;v·F=39,844W (1)

在分析过程中，认为钢轨和车轮的材料是相同的，并假定产生的热量会在相互滑动的元件之间均匀地消散。所以两个接触分量的热量分配(a)都是0.5。(为了得到更精确的计算结果，对前五次轨道侧转建立了单独的瞬态热量有限元模型。为了得到相同的接触时的温度结果，假设第一周转动时钢轨的热量分配为0.52，则第一次旋转时轮轨的热量分配为0.48，第五次旋转时轮轨的热分配为0.54/0.46。本文后面没有考虑这些变化值。)因此落在车轮上的热能为:

Qk =alpha;·Q=19,922W (2)

假设热源沿整个接触面积A均匀分布，热通量为 [17]:

q = Qk /A=2.013·10 ^8·(w/msup2;) (3)

将计算得到的热通量q分配到有限元模型中，如图5所示，120段中始终有12段处于活动状态(根据接触面积得出)，从而保证了与接触面积大小对应的热量输入被指定。热源由1mm的时间位移控制(与车轮外周速度85km/h相符)。当区域测试结束时，被关闭一个周期的热源就会过期。

在模型中除了增加热流密度

全文共10168字，剩余内容已隐藏，支付完成后下载完整资料

资料编号：[1449]

您可能感兴趣的文章

• 流化床包衣造粒过程的监测与控制研究外文翻译资料
• 一种新颖的旋转流化床包衣细颗粒涂层的方法外文翻译资料
• 中国城市垃圾的处理和管理外文翻译资料
• 滤袋、气旋、和湿式除尘方法在真空吸尘器中的比较外文翻译资料
• 一个灵活的模型辗环机设计外文翻译资料
• 带有柔性转子的主动电磁轴承系统的识别外文翻译资料
• 柔性阻尼支承下转子振动特性实验外文翻译资料
• MapReduce:超大集群上的数据简化处理外文翻译资料
• 垂直循环式立体车库的停车与乘车调度优化外文翻译资料
• 高灵敏度、高稳定性的自温度补偿电涡流位移传感器外文翻译资料