
英语原文共 9 页,剩余内容已隐藏,支付完成后下载完整资料
同步带疲劳损伤预测
绳索力学是通过简单弯曲的力学分析去研究同步带的疲劳失效机理。为了计算同步带在扭矩传递条件下的曲率量,我们提出了一个简化梁模型,尤其是将作用在工作侧面上的摩擦力的影响用于解释带齿啮入和啮出时啮合部分的累积损伤之间的差异。最后,根据计算的曲率在驱动接触和从动接触疲劳破坏条件下进行疲劳寿命预测。
1引言
同步带疲劳失效是十分复杂的,因为带的失效受很多因素影响(小山,1978;amijima,1989)如紧边、松边张力,带轮直径,带的节距,带与带轮之间的间距不同,带的刚度、包角等。由于疲劳条件不是任何影响因素的单一函数,因此,单独的使用扭矩或齿载荷参数判断疲劳损伤并不合理(Childs,1991)。此外,皮带是由橡胶、纱布和线绳组成的复合结构,即使是在每个元素下单独求解也是复杂的,并且因为疲劳过程中存在的化学变化,以及复杂的几何非线性变形行为(科斯特洛,1990;赫尔,1969)致使失效机理还没有被充分的发掘(福盛,1992)。
因此,在同步带上,由于啮合条件和材料因素的不同,出现了许多失效模型。Koyama等人(1978)提出了梯形齿同步带的三种主要疲劳失效模型:第一种是拉伸构件断裂,第二种是齿形剪切,最后一种是磨损。达尔加诺等人(1994)提出了圆齿同步带失效模型。目前普遍认为,在正常的汽车凸轮轴驱动条件下,齿形剪切是主要的失效模型。
为了获得合理的寿命预测参数,需要进行详细的失效机理研究。Childs(1997, 1991)的研究集中于同步带在啮入和啮出带轮时的啮合与非啮合阶段产生的额外负荷或变形。lizuka等人(1994)对同步带失效机理进行了一些基础研究,并报道了两种附加失效模型:第一种是齿根开裂模型,第二种是线绳失效模型。应力集中靠近齿根是前一模型的主要影响因素,而线绳弯曲(lizuka等人,1995年,1995b;lizuka和Gerbert,1996)是后者模式的主要影响因素。
在这项研究中,通过分析线绳的受力情况,得出了曲率和线绳失效之间的关系。并且提出了一种简化的带式弯曲梁模型,得到了啮入和啮出部分在啮合条件下的曲率方程。因此,寿命预测是基于计算的最大曲率进行的。
2线绳弯曲
2.1基本理论
线绳弯曲基本模型早已被提出,(Gerbert,1975)。本文的主要目的是分析线绳受拉和弯曲时的力学性能。为了方便起见,在这里总结了这种方法。在本节后面将扩展模型,以更好地处理弯曲过程中出现的剪切应变。
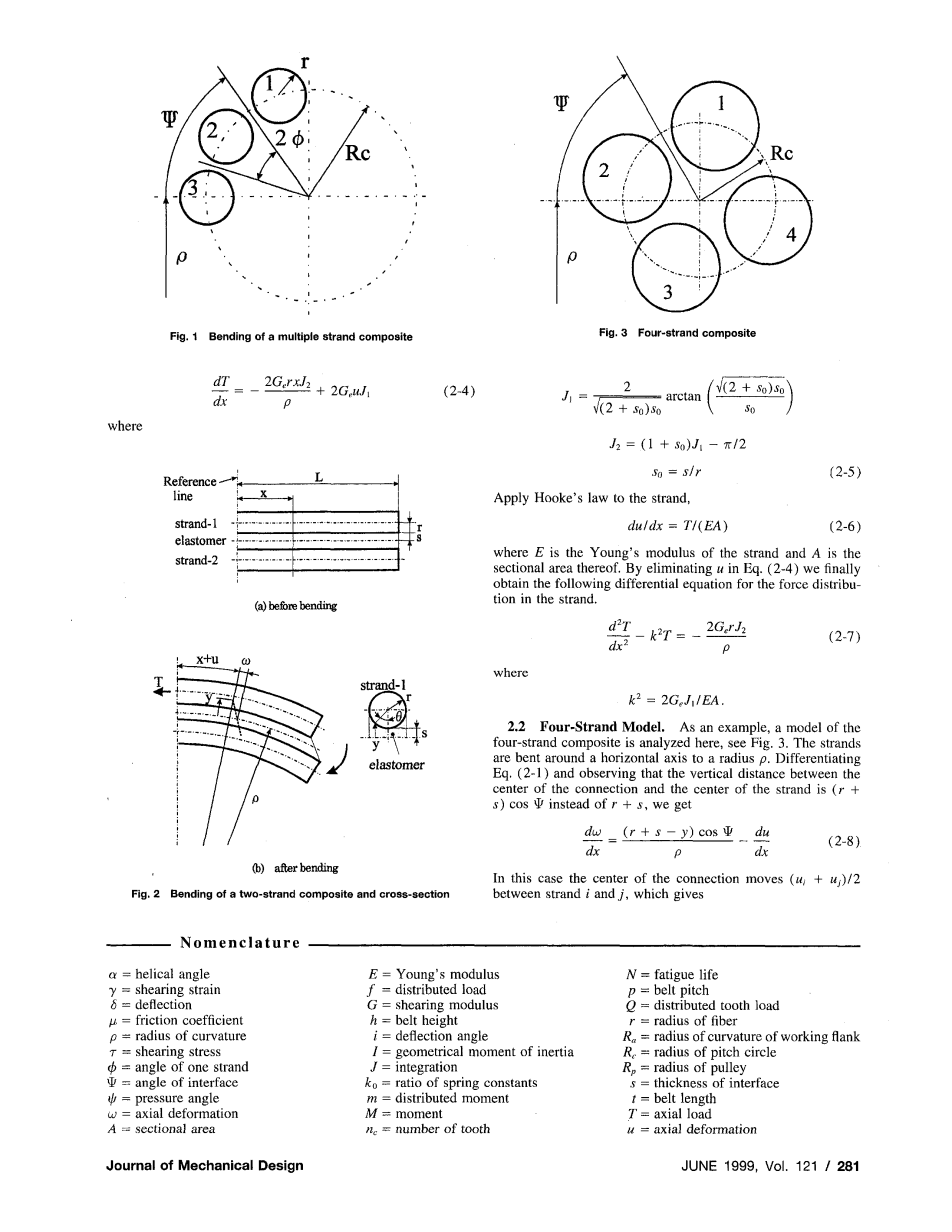
图1一个多股复合弯曲
多股复合材料如图1所示,圆代表我们使用的线绳(半径r),为了简化所以没有设置中心的核心线绳。每个线绳之间的位置由角Psi;和2Phi;的倍数给出。多股线以半径rho;绕着带轮轴心放置。如线绳1和2之间的连接部分弯曲半径是(rho; Rc sinPsi;)但是一般来说,Rclaquo;rho;,所以对于所有连接我们都可以使用弯曲半径rho;。
图2两股复合材料的弯曲及截面
首先考虑两根与柔软的弹性体相连的线绳,这些弹性体使两股线相隔2s,见图2(a)。当这个复合物弯曲半径为rho;时,我们得到了图2中所示的几何形状。弯曲状态相对于弹性体的中心线是反对称的。上层处于拉伸状态,下层处于压缩状态。因此,只需要处理上层线绳即可。假设我们的弹性体中只存在剪切应力。这些剪切应力被转移到线绳上,并且规则的叠加在弯曲应力上。图2还显示了一个线绳的横截面。当线绳是直的,沿着参考线取长度为x的弹性体。弯曲后,在同一位置线绳伸长,见图2。在y位置的压缩应变是(r s-y)/ rho;。所以在距离x的位置上的压缩应变是x(r s-y)/ rho;,下面给出弹性体的剪切变形公式:
由于剪切应变gamma;=omega;/y,胡克定律给出了下面的剪切应力的剪切模量Ge,
在图2(b)中Y = S R(1-COS(theta;))。沿线绳取最小长度dx可得出:
因此,
将胡克定律应用于线绳,
其中E是线绳的杨氏模量,A是其截面面积。通过在等式(2-4)中消除u,我们最终得到了绞线中力分布的微分方程。
其中
2.2四股模型
图3四股复合材料
作为例子,在这里分析了四股复合材料的模型,见图3。线绳以半径rho;绕带轮轮心弯曲。由微分等式(2-1)观察得出连接中心与线绳中心之间的垂直距离为(r s)cospsi;,而不是r s。得出:
在这种情况下,连接体的中心在线绳i和j之间移动了( u i u j)/ 2,由此得出:
其中,alpha; =螺旋角gamma; =剪切应变delta;=挠度mu;=摩擦系数rho;=曲率半径tau;=剪切应力Phi;=一个线绳的角Psi;=倾角psi;=压力角omega;=轴向变形A=截面积
E =杨氏模量f=分布式负载G =剪切模量h =带高度i =偏转角度I =几何惯性矩J=集成k0 =比弹簧常数m =弯矩M =时刻nc=齿数
N疲劳寿命p =带节距Q =分布齿载荷r =纤维半径Ra=工作侧曲率半径Rc=螺距圆半径Rp=齿圈半径s=界面厚度t =带长T =轴向载荷u=轴向变形
对于线绳2,我们对两个连接体(分别在线绳1和2之间以及在线绳2和3之间)施加力,通过计算总力可得出:
使用式(2 - 9)和(2 - 10),我们得到关于Ti的微分方程,代入x=Psi;RC/COS(alpha;) ,alpha;是线绳螺旋角。Rc = (R S)。因为没有纵向合力,所以T3=- T,T4 =-T2最终得到微分方程:
求解简单弯曲的方程并考虑下列边界条件:
整理式(2-9),我们得到如下剪切应变方程:
其中alpha;= 80°,r=0.0045 mm,s=0.0015 mm,Rc=0.0085mm,rho;=30mm。
右边的第一个分式与曲率有关,并且在所有的多线绳模型中均是如此。然而,第二个分式与线绳伸长有关,并且受线绳股数的影响。图4显示了一个计算示例。它是函数sin(Psi;),最大剪切应变发生在Psi;=pi;/2和3pi;/2处获得,即发生在垂直方向上。lizuka等人。(1994b)发现线绳沿玻璃纤维线绳之间的垂直界面失效。这一现象可以用剪切应变依赖关系来解释。
图4四股模型剪应变与角Psi;的关系
式(2-14)中,因为线绳的杨氏模量E很大同时延伸量u非常小,所以第二个分式可以省略不计。因此,我们得到如下近似方程:
由此知,gamma;12的值与曲率成比例。
2.3四股线绳模型
图5带绳示意图
图5是四股线绳模型的示意图。多根线绳组成绳股,其中每股包含四根线绳。绳股之间的联系很弱,因此每根独立弯曲曲率为1 / rho;(尔贝特,1975)。由此,我们得到相同的方程为式(2-13),每一个线绳的张力为Ti。假设x =Psi;CRC/COS(alpha;),我们得到介于纤维f2和f4rsquo;之间的剪切变形omega;24rsquo;如下:
其中rf是线绳的半径,2ss是股线之间的界面厚度。最终剪切应变为:
因为杨氏模量很大,第二个分式通常只有第一个数的百分之几。因此,我们得到近似方程如下:
因此,我们可以使用式(2-18)得出的曲率计算多股束模型的剪切应变。
3带弯曲的梁模型
图6驱动轮,紧边,同步带与带轮的啮合
我们主要研究紧边啮合的第一齿,分析弯曲力的大小。图6显示了8mm宽同步带的带轮槽和带齿之间的紧密啮合情况。该模型考虑的是底部平面-1到达(或离开)轮齿顶面的啮入(或啮出)之前(或之后)的情况。图7显示的即是啮合时的力学分析;皮带张力为Tt,轮齿载荷为Q1、工作齿面的摩擦力为mu;Q1,带轮底面与皮带齿尖接触处的分布载荷为fb, mu;Q1的方向随啮入和啮出的条件而改变,因为mu;Q1值是由皮带齿和带轮槽的相对运动引起的。
图7进入和退出条件下带的弯曲模型
图8在紧侧张力下第一次啮合时皮带弯曲的简化梁模型
图8显示了皮带弯曲的简化梁模型。mu;Q1的影响被认为是分时刻的,在t3区域mmu;=mu;Q1Ra/t3,其中Ra是工作齿面的曲率半径。正标志为啮入,负标志为啮出。齿负荷Q1被分为等值的组成部分,切向分量fn=( Q1sin(psi;))/t3,x轴方向ft=( Q1cos(psi;))/t3。切向分量被认为是分布矩m=ftht=mt,m的最大值在x=t1 t2处,其中ht是齿高,在x=0处m=0。在每个简化区域内弯曲刚度被认为是恒定的·。根据梁理论,基本方程是:
其中E是杨氏模量,Ii即转动惯量,M是弯矩,rho;是曲率半径。在每个区域,我们有如下的Mi:
其中delta;是x=t0出的偏移量。联合等式(3-1)和(3-2),我们得到微分方程:
其中beta;2=TT/EIi,fi(x)是已知的x的函数,边界条件如下:
Tt= 800 N,tau;s= 50 N,和Rp = 28.14mm。其他数据:mu;= 0.2,Phi; = 30°,Ra = 2.2mm,E= 10 MPa和I 1= I 2 = I 3。
A,B,gi(x)和delta;显示在附录中。我们从式(3-1)和(3-5)得到曲率为1/rho;。
曲率的大小与mt和mmu;有关。因此,对Q1的估值对于研究曲率的性质十分重要。Q1的大小受同步带紧侧张力、侧边张力、带轮节距和直径等因素的影响。在这项研究中,我们使用了Gerbert的方程(1978)。方程修改如下
其中Tt和Ts,是紧和松边张力,Ti是同步带需要伸展去适应带轮的节距所需的张力,K0是带齿和带轴间的弹性常数比例,nc是接触齿数。
图9 在驱动轮周围的HTD皮带的曲率分布
图9比较了计算值并实测了沿带方向曲率的分布(lizuka等人,1995)。沿着带方向的距离分布与图6中所示的相同。所得到的计算结果I 1= I 2 = I 3的获得源于沿轴向的曲率的基本分布。我们用Ii= 19.75(1.53 3.53)/ 3mm4,其中 19.75mm是带的宽度,1.5mm和3.5mm是橡胶厚度,带齿的高度t1假定是2.15mm,t2是2.2mm, t3是3.5(pi; / 6)= 1.75mm,相应的近似等于于面宽和齿长。假设齿高R0为2.2 mm,是带齿宽度的一半。实验曲线和解析曲线的分布曲线相似。最大曲率在x=t1 t2处获得。实验中,在x = 1.5mm处的极大值是由该带的截面积的变化所引起I1的变化所导致的(lizuka和Gerbert,1996)。
,
图10 在x=t1 t2的最大曲率和紧边张力之间的关系
(其中mu;是摩擦系数。Ts=50N,Rp=28.14mm,Ra=2.2mm,E=10MPa,I 1= I 2 = I 3)
图10显示了摩擦
全文共10695字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[15777],资料为PDF文档或Word文档,PDF文档可免费转换为Word


