
英语原文共 14 页,剩余内容已隐藏,支付完成后下载完整资料
惯性传感器、全球定位系统和测程法
作者:Gregory Dudek(格雷戈里·杜德克)、Michael Jenkin(迈克尔·詹金)
引言:本章探讨了如何利用世界的某些特性来开发一个机器人或其他装置,以建立其自身运动或姿态(位置和方向)的模型,与外部参照系相关联。尽管这对于许多自主机器人系统来说是一个关键问题,但是建立和维护移动代理的定位和位置估计的问题在陆地导航中有着悠久的历史。
20.1测程法
单词odometry是希腊词“hodos”意思是旅行或旅程和“metron”意思是量度或尺寸的缩写词。考虑到各种各样的土木工程应用武力征服它的重要性,测程法已经研究了超过2000年的基本概念。 也许最早提到测距法的内容出现在维特鲁威的建筑十本书中,其中他描述了一个由我们的前辈传递的最有创造力的有用发明,它使我们坐在马路上或海上航行时, 知道我们已经完成了多少英里的旅程[20.1]。在自主车辆的情况下,测距通常指的是使用来自致动器(车轮,踏板等)的数据来估计车辆的整体运动。 基本概念[20.2]是建立一个数学模型,说明车辆的车轮,关节等的选定运动如何引起车辆本身的运动,然后随着时间的推移整合这些指定的运动,以便开发姿态模型作为时间的函数的车辆。作为一个时间的函数,里程计信息用来估计车辆姿态被称为航位推算或演绎推算,并在海上航行中得到广泛应用[20.3]。
y
omega;
ICC
upsilon;r
V
theta;
x
upsilon;l
d
图20.1 差动传动运动学
a)
b)
L = Iomega;
Spin axis
S
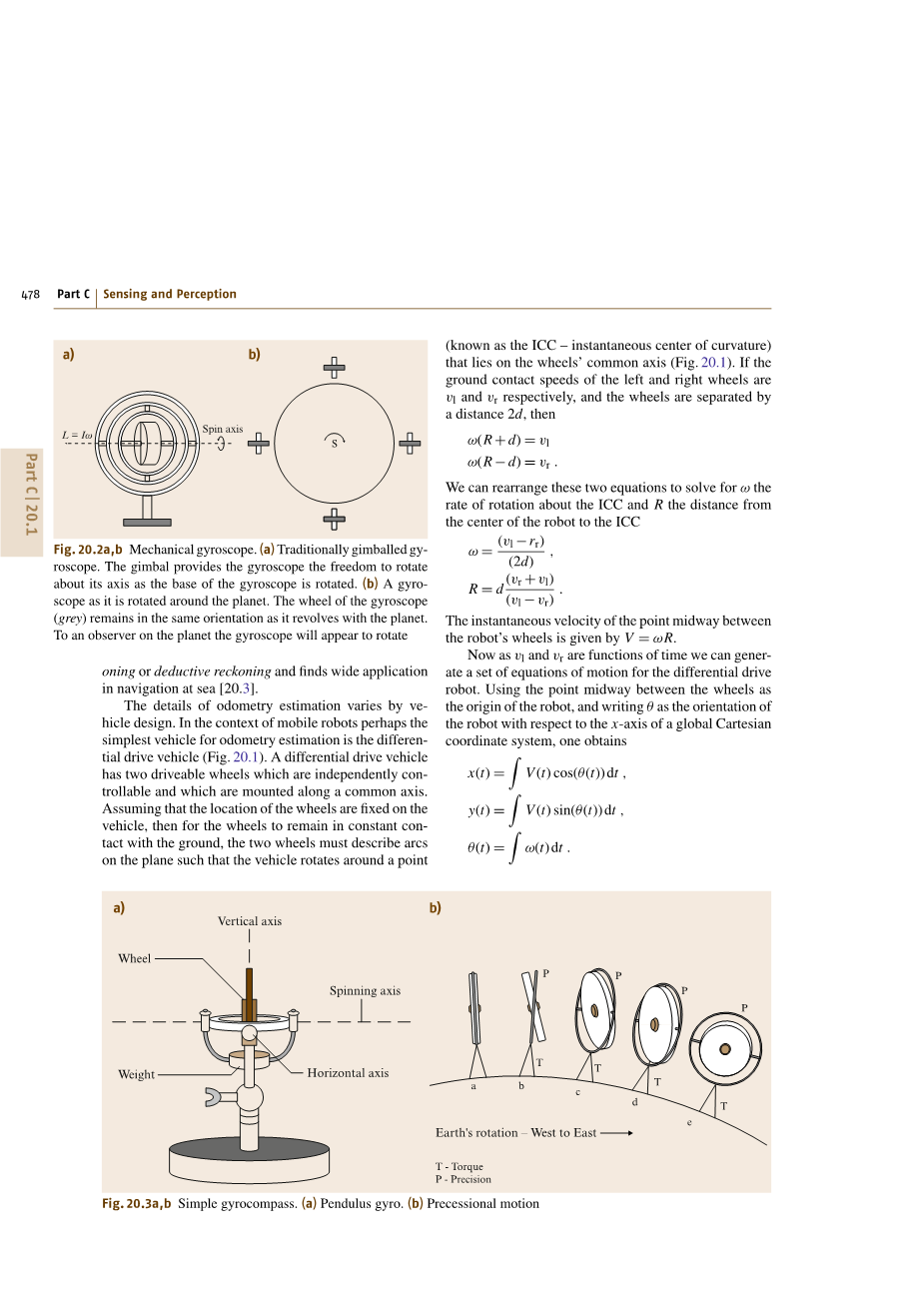
图20.2 a,b机械陀螺
- 传统的万向陀螺。当陀螺旋转时,万向架提供陀螺仪自由旋转其轴线的自由度。
- 它是围绕着星球旋转的陀螺仪。陀螺仪的轮子(灰色)保持与地球旋转方向相同的方向。对于这个星球上的观察者来说,陀螺仪会出现旋转。
测程法估计的细节因车型设计而异。 在移动机器人的情况下,测距估计最简单的工具就是差速驱动车辆(图20.1)。 差速驱动车辆具有两个可独立控制的并且沿共同轴安装的可驱动轮。 假设车轮的位置固定在车辆上,那么为了车轮与地面保持恒定接触,两个车轮必须描述平面上的弧线,以便车辆绕着一个点旋转(称为ICC - 瞬时曲率中心),位于车轮的共同轴线上(图20.1)。 如果左右车轮的地面接触速度分别为vl和vr,并且车轮分开距离2d,则
我们可以重新安排这两个方程组的求解omega;的旋转速度对ICC和R从机器人中心到ICC的距离
该点的瞬时速度在机器人的车轮之间由v=R计算
现在,VL和VR是时间的函数我们可以说吃了一套差动驱动机器人的运动方程。使用点中间车轮作为机器人的起源,写theta;作为相对于全局笛卡尔坐标系的X轴的机器人定位,获得
,
,
。
a)
b)
Vertical axis
Wheel
P
P
Spinning axis
P
P
T
Weight
Horizontal axis
T
a
b
T
c
d
T
e
Earth#39;s rotation – West to East
T - Torque P - Precision
图20.3 a,b 简单的回转罗盘 (a)陀螺旋转 (b)旋进运动
这是飞机上差速驱动车辆测距的解决方案。 给定控制输入(v1和vr)和一些初始状态估计,我们可以在任何时间t估计理想化机器人的状态。
给定这样一个模型和控制输入的完整知识,原则上,我们应该能够随时估计机器人的姿态。在完美的世界里,这将是准确估计未来机器人姿态的所有必要条件。不幸的是,在建模(车轮尺寸,车辆尺寸的不正确估计),控制输入的不确定性,电机控制器的实际情况(指令车轮旋转和真实旋转之间的误差),机器人物理建模错误(车轮压实,地面压实,车轮滑动,非零轮胎宽度)等,引起车辆运动的航位推测估计与其真实运动之间的误差。纠正这个错误的问题是车辆姿态维护的问题,并且需要将航位推算估计与从其他传感器系统获得的估计相结合。
本手册中的其他章节(例如第21-24章)将检查依赖外部事件(视觉和其他方式)的传感器,这些传感器可以提供有关机器人姿态或其姿态变化的信息。在这里,我们考虑传感器在外力和物质性质的影响下使用全球定位系统(GPS)来传导物质的物理特性。
20.2 陀螺系统
陀螺仪系统的目标是通过利用旋转下产生可预测效果的物理定律来测量车辆定向的变化。 旋转框架不是一个惯性框架,因此许多物理系统似乎表现为非牛顿形式。 通过测量这些与牛顿框架预期的偏差,可以提取潜在的自转。
20.2.1 机械系统
机械陀螺仪和陀螺罗盘在导航方面有着悠久的历史,BBohnenberger通常被认为是陀螺仪的第一个记录结构[20.4],并且在1851年,Leacute;onFoucault将陀螺仪视为惯性坐标系。 1885年,电罗经由Martinus Gerardus ven den Bos获得专利。1903年,HermanAnschuuml;tz-Kaempfe建造了一个工作陀螺仪,并获得了设计方面的专利。 1908年,埃尔默斯佩里在美国获得专利,并试图将该设备出售给德国海军。 随后发生专利争夺战,爱因斯坦在案件中作证。(有关陀螺罗经及其发明者历史的更多详情,请参见[20.5-8]。)
陀螺仪和陀螺罗盘依赖于角动量守恒原理[20.9]。 角动量是在没有外部扭矩的情况下,旋转物体围绕相同旋转轴以相同角速度继续旋转的趋势。 惯性矩I以角速度omega;旋转的物体的角动量L由下式给出
考虑一个安装在轴上的快速旋转轮,以便它可以自由地改变其旋转轴(图20.2a)。假设由于空气阻力或轴承而没有摩擦,无论外部保持架的运动如何,转子轴将保持恒定。尽管通常不希望直接通过陀螺仪使用角动量守恒原理,但是可以利用这种定向恒定性来独立于车辆的运动来维持方位。为了看到这一点,假设在赤道上放置一个陀螺仪,其旋转轴沿着赤道对齐(图20.2b)。当地球旋转时,陀螺仪将保持恒定的定向轴,因此地球固定的观察者将会旋转,每24小时返回其原始方位。类似地,如果陀螺仪定位在赤道上,使其旋转轴线平行于地球的旋转轴线,则陀螺仪的旋转轴线将保持静止并且似乎对于固定在地球的观察者保持静止,因为行星旋转。
尽管这种全局运动限制了机械陀螺仪直接感测绝对方向的能力,但陀螺仪可用于测量方位的局部变化,因此非常适合车辆机器人应用。 速率陀螺(RGs)测量车辆的旋转速率(其旋转角速度)。 这是所有陀螺系统基础的基本测量。速率积分
为了利用陀螺仪相对于地球稳定框架进行导航,希望轴的旋转轴线保持固定在地球框架内,而不是相对于外部框架保持固定。一个陀螺罗盘通过依靠进动获得这个。当施加扭矩来改变旋转物体的旋转轴时,角动量守恒将导致垂直于角动量和扭矩施加方向的旋转方向的变化。这是导致悬挂在一端的陀螺仪绕着它们被悬挂的端部旋转的效应。考虑图20.3a中勾画出的Pendulus陀螺仪。这是一个重量悬挂在旋转轴下方的标准陀螺仪。像以前一样,设想这个悬摆罗经在赤道上旋转,旋转轴线与行星旋转轴线对齐,并且重物直接向下悬垂。随着行星旋转,陀螺仪的旋转轴线保持静止,并且在行星旋转时似乎保持静止。现在假设不是与行星的旋转轴对齐,旋转轴与赤道对齐。随着行星旋转,旋转轴被拉出平面,因为它保持与原始旋转轴对齐。当它从平面上被拉出时,悬挂在罗经下方的质量被抬起并且由于重力而产生扭矩下降。垂直于自旋轴的方向和转矩将旋转轴旋转离开已知的方向并朝向真实的极点。这个过程如图20.3b所示。
a)
Start
End
b)
Start End
alpha;
图20.4 a,b 环形光路 (a)固定路径 (b)移动路径
不幸的是,摆式陀螺仪并不是一个理想的导航设备。虽然它的旋转轴与行星的旋转轴是一致的,但它并不会直接向这个值收敛,而是在它周围振荡。这个阻尼问题的解决方案是利用油藏,而不是固体重量,作为平衡,并限制油藏的运动[20.10]。
陀螺罗盘通过控制陀螺仪的进动来找到真北。在实际中,机械陀螺罗经的性能受到作用在罗盘上的外力的影响,这也有助于陀螺仪的进动。这包括由包含陀螺仪的装置的运动产生的力,以及作用于车辆上的任何外力。另一个关于机械陀螺仪的问题是,在远离赤道的纬度上,陀螺仪的稳定位置不是水平的,在这样的纬度上准确的估计是正确的,这需要修正到原始的陀螺罗经值。最后,机械陀螺仪需要一个外力来保持陀螺仪的旋转。这个过程将不必要的力量引入到系统中,从而进一步破坏测量过程。
由于它的复杂性、成本、尺寸、旋转罗盘的微妙特性,以及更便宜、更可靠的技术,机械陀螺已经被光学和微型机电系统(MEMS)系统所取代。
20.2.2 光学系统
为了测量(相对)航向,光学陀螺仪依靠萨格纳克效应而不是旋转惯性。 该机制基于旋转框架中光学驻波的行为。 从历史上看,这是首次使用激光和镜面布置产生的,但现在通常使用光纤技术获得。 萨格纳克效应以其发现者乔治萨格纳克命名[20.11,12]。 其基本概念甚至可以追溯到Harress [20.13]的工作,并且可能在地球自转的测量方面发现其最着名的应用[20.14]。
忽略相对论效应并考虑图20.4a所示的圆形光路。如果两个光脉冲在周长D =2pi;R的固定路径周围以相反的方向发送,它们将以相同的速度行进相同的距离。它们将同时到达起点,取时间t = D / c(其中c是介质中的光速)。现在让我们假设这个圆形光路不是静止的,而是以转速omega;为中心顺时针旋转(图20.4b)。围绕路径顺时针行进的光线必须走得更远才能到达起点,而沿着路径逆时针方向行进的光线走向更短的距离。顺时针路径的距离为Dc =2pi;R omega;Rtc,其中tc是顺时针方向所用的时间,而逆时针路径的距离为Da =2pi;R-omega;Rta,其中ta是逆时针方向所用的时间。但是Dc = ctc和Da = cta,所以tc =2pi;R/(c-omega;R)和ta =2pi;R(c omega;R)。时间差Delta;t= tc-ta由下式给出
通过测量Delta;t,可以计算转速。 请注意,尽管上述推导假设经典力学并忽略了相对论效应,但当考虑相对论速度时,推导也适用[20.15]。 参见[20.16]对萨格纳克效应和环形激光进行深入的回顾。
在光学陀螺仪中,激光器通常用作光源。 光学陀螺仪采用直线光路与镜面或边缘棱镜来引导光束(环形激光陀螺仪-RLG)或保偏玻璃光纤环路(光纤陀螺-FOG)。 玻璃纤维实际上可能会多次循环,从而延长了光路的有效长度。 通过检查顺时针和逆时针光信号之间的相位干涉来检测顺时针和逆时针方向之间的时间延迟。 为了测量三维(3-D)旋转,可以将多个非平行轴的光学陀螺仪组合在一起。
可以使用各种技术来测量这两条路径之间的时差,包括检查由于陀螺运动引起的激光的多普勒(频率)偏移,以及在顺时针和逆时针路径之间检测干涉图样的拍频[ 20.17 ]。环形干涉仪通常由许多光纤线组成,它们在回路的相反方向上传导固定频率的光,并测量相位差。环形激光器由环形形状的激光腔组成。光在这个腔的两个方向上循环,产生两个驻波,两个方向上的节点数目相同。由于光路长度在两个方向上不同,所以谐振频率不同。测量了这两个频率之间的差异。环激光方法的一个不幸的副作用是,两个信号在小旋转时相互锁定,通常需要以受控的方式物理旋转该装置,以确保这种锁定效应是可以避免的。
20.2.3 微机电系统
几乎所有的微机电系统(MEMS)陀螺仪都是基于振动机械元件来感知转动的。振动加速度计依赖于科里奥利加速度的振动模态间能量传递。科里奥利加速度是指在旋转参照系中产生的表观加速度。假设物体在旋转的参照系中沿直线运动。对于惯性框架中的外部观察者来说,物体的路径是弯曲的——因此,在旋转观察者看来,物体上必须有一定的力以维持直线运动。物体在一个局部速度V直线在架率Omega;相对于惯性系旋转将经历由科里奥利加速度
在MEMS陀螺仪传感加速度等于诱导局部线性速度和测量所产生的科里奥利力。
早期的MEMS陀螺仪利用振动石英晶体产生必要的直线运动。最近的设计已经用硅基振动器取代了振动石英晶体。已经开发了各种MEMS结构,包括下面所描述的结构。
调谐音叉陀螺仪
音叉陀螺仪使用音叉式结构(图20.5)作为底层机构。当音叉振动在旋转框架,科里奥利力引起的振动了叉子叉的平面,已经被测量出来。这是惯性立方体传感器[ 20.18 ]所使用的效果。
振动轮陀
全文共17765字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[11782],资料为PDF文档或Word文档,PDF文档可免费转换为Word


