基于小尺寸试验数据的全尺寸电缆桥架火焰的数值模拟
Tarek Beji amp; Bart Merci
摘要:
本文提出了一种基于计算流体力学(CFD)的电缆桥架火灾发展预测建模方法。该方法适用于5个一组的水平桥架(每个长2.4米,宽0.45米),垂直间距为0.3米,并靠墙设置。每个桥架上装有49根PVC电源电缆。由一个在最低桥架正下方0.2米的80千瓦丙烷燃烧器点火。每个塔板(由一种均匀材料制成)上承载四组电缆。这些电缆由纵向的空气槽分隔,以模拟它们相对松散的排列方式。利用锥形量热仪(CC)估算了电缆材料的热性能和表面点火温度。当点火温度达到时,电缆根据从CC获得的规定的单位面积热释放率(HRRPUA)剖面,作为其本身原始或修改后的形状燃烧。从而预测一个真实的火焰模式。此外,仅使用CC的数据,峰值HRR被低估,使得达到峰值的时间被高估。改进后的HRRPUA CC剖面设计大大提高了结果的准确性。
关键词:电缆桥架火灾,计算流体力学(CFD),锥形量热法
1 前言
自1975年布朗斯费里核电站(Browns Ferry Nuclear Power Plant, NPP)发生火灾以来,人们对理解和预测电缆桥架火灾的发展有着浓厚的兴趣。电缆桥架实际上是核电站可燃负荷的一个重要组成部分,它们还储存在城市电力传输的隧道(即电缆隧道)中,或储存在电信系统和数据中心的中央办公室中。
预测一堆电缆槽的热释放率(HRR)现在仍然是一个非常具有挑战性的任务由于问题的固有的内在复杂性,这源于电缆的排列(如多个托盘,每个包含大量的电缆松散或紧密地排布)以及它们的物理和化学性质(如非均质的材料和复杂的降解过程)。根据托盘装载量(TL),即托盘中电缆占用的体积与国家消防协会(NFPA)规定的最大值NEC max之间的比值,确定松散或紧密排列的类型。例如,对于本文中考虑的场景,TL = 48%,是一种松散的安排。Askit等人指出,电缆的配置对火灾响应的影响可能与电缆的物理和化学特性一样重要。此外,在FIPEC(电缆防火性能)项目中,强调了电缆的装载、捆绑、分组和间距对火焰蔓延程度以及火灾的严重程度的影响。
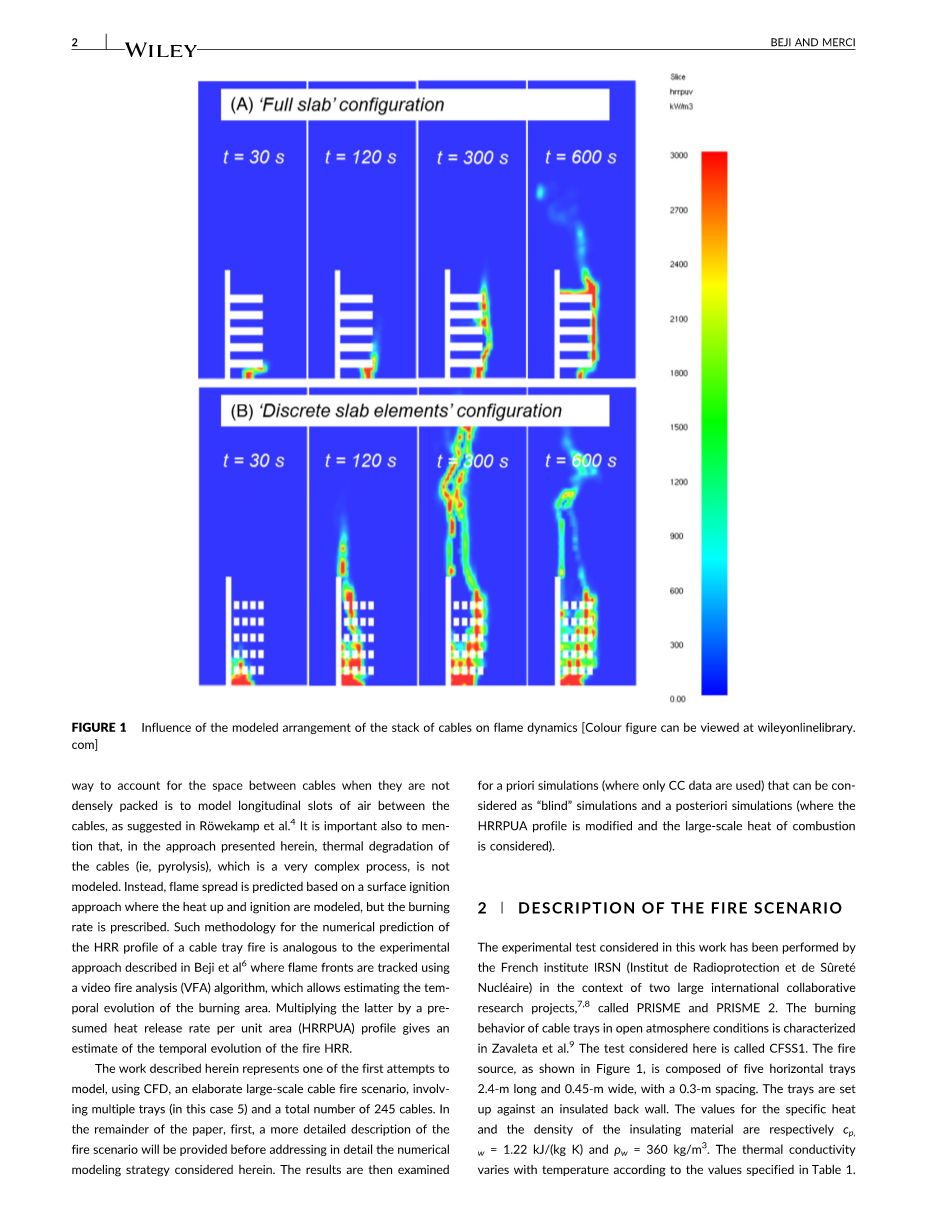
通常,电缆桥架被描绘成一个单一的矩形板,并定义燃料在燃烧前经历热解过程的材料表面。然而,这种方法不能复现真实的火焰模式。例如,如果有多个水平桥架,电缆排列松散,底部点火,火焰将穿透桥架,导致垂直(从一个托盘到另一个托盘)和水平火焰同时蔓延。如果每个托盘都建模为一个均匀的矩形板(参见图1),情况就不是这样了;但如Rouml;wekamp等人所建议的通过建立电缆之间的纵向空气槽模型来模拟松散排列的电缆之间的空间,可以解决这一问题。还需要指出的是,在本文提出的方法中,没有对电缆的热降解(即热解)这一非常复杂的过程进行建模。相反,火焰传播是基于表面点火方法预测的,即建立升温和点火模型,规定燃烧速率的方法。这种电缆桥架火灾HRR剖面数值预测方法类似于Beji等人描述的实验方法,即使用视频火灾分析(VFA)算法跟踪火焰前沿,该算法可估计燃烧区域的时间演化,后者乘以单位面积热释放率(HRRPUA)的假设剖面,就可以估计火灾HRR的时间演化。
图1 堆叠布置模型对火焰动力学的影响
本文描述的工作是首次尝试利用CFD模拟复杂的大规模电缆火灾场景,涉及多个托盘(在本例中为5个)和245根电缆。在本文的其余部分中,首先,在详细描述本文所考虑的数值建模策略之前,将对火灾场景进行更详细的描述;然后对结果进行先验模拟(只使用CC数据)和后验模拟(修改HRRPUA剖面并考虑大规模燃烧热)。
2 描述火灾场景
在这项工作中考虑的实验测试是由法国IRSN研究所(核辐射防护和核安全研究院)在两个大型国际合作研究项目PRISME、PRISME 2的背景下进行的。Zavaleta等人描述了露天条件下电缆桥架的燃烧行为,这里涉及的试验称为CFSS1。火源如图1所示,由5个长2.4米、宽0.45米的水平托盘组成,间距0.3米,且托盘靠在绝缘的后墙上。绝缘材料的比热容和密度分别为=1.22 kJ /(kg K)和= 360kg/m3。导热系数随温度的变化如表1所示。
表1 绝缘材料的导热系数随温度的变化表
绝缘材料的热性能已经在数值模拟中规定(在两个中间温度之间对kw进行线性插值),且厚度为5cm。每个托盘包含49根13mm外径的聚氯乙烯电缆,由PRISME合作伙伴芬兰技术研究中心(VTT)提供。每根电缆由以下材料组成:(1)单位长度质量为85 g/m的金属材料;(2)线性质量为85 g/m的护套层;(3)线性质量为35 g/m的填料层;(4)30g/m的隔热层。点火源是一个0.30.3de 砂燃烧器位于第一个(即最低)托盘下方0.2米的中心位置。该燃气燃烧器,供应丙烷,提供了80 kW的火力。当总HRR达到400 kW时停止供应,对应时间为80秒。
3 数值模拟
利用火灾动力学模拟器(FDS 6.5.3)对上述火灾场景进行了数值模拟,这个模拟器是为模拟低马赫数流体流动而开发的CFD代码,其重点是火灾产生的烟和热的传输。在FDS中,采用二阶有限差分数值格式求解Navier-Stokes方程。通过求解一维傅里叶热传导方程,计算了壁面的热损失。除了前面提到的,FDS 6.5.3中的所有默认常量和子模型都已使用。
后面将提供更多的数值建模细节。
3.1 化学和燃烧
PVC是火灾中的主要燃料。假设气相燃烧反应为单步混合控制反应,表达式如下:
Fuel(Cl) Air ( ) → Products (HCl O
C CO C ) (R1)
、和的化学计量摩尔分数分别是,, C,CO和烟尘。这些系数取值为= 1.545;= 5.809;= 0.99; = 0.11;= 0.90。
更具体地说,CO和烟尘的摩尔分数是根据它们的产率yi来计算的:vco = yco; vc = yc (1)
MW是分子质量。
根据本文所考虑的电缆锥形量热法(CC)测量,CO产率取= 0.05。未用CC测得的产烟量取自Tewarson为= 0.172。其余的化学计量系数是根据原子平衡计算的。
从锥形量热法测量平均有效燃烧热Delta;Hc = 17.7 MJ/kg。接下来所进行的模拟以规定的基于17.7 MJ/kg的锥形量热计为基础,标记为先验模拟。然而,根据同时测量的质量损失率和热释放率,在大规模试验中燃烧热测定为22MJ/kg。考虑后一个值的模拟称为后验模拟。
燃烧模型是基于涡流耗散概念建立的(EDC)。
3.2 湍流
湍流模型是建立在大涡流模拟(LES)的基础上的,现有的湍流粘度模型有四种:修正的Deardorf模型、Vreman模型、定常 Smagorinsky模型和动力学 Smagorinsky模型。前者是默认模型。
3.3 辐射
采用有限体积法(FVM)求解辐射传递方程(RTE)。规定(默认情况下) 辐射分数为一个下界, 是为了限制辐射计算中由于温度场的不确定性而产生的不确定性。在当前的工作中,PVC的辐射分数= 0.456,取自Tewarson的小规模的测量结果。
3.4 火焰蔓延的建模
3.4.1 几何简化和升温点火建模
第2节中描述的电缆线架堆叠是一个非常复杂的燃料组件,其中火焰蔓延的预测(尽管使用相当简单的点火协议)尤其具有挑战性,主要有两个原因。
第一个原因是燃料是由直径约1cm的离散元件(即电缆)组成的,这比在大规模火灾的CFD模拟中通常可以承受的单元尺寸小一个数量级。此外,电缆松散地排列在每个托盘中,因此不能将每个托盘视为是均匀的平板,这将使火焰偏离,如图1A所示。火焰更愿意穿透托盘,如图1B中5个托盘的结构所示。
第二个原因(这使得现在的配置在建模方面具有挑战性)是与热解和火焰蔓延建模相关的固有困难,例如,选择适当的热性能。
本文所描述的火焰蔓延建模策略依赖于几何化简,并与基于表面升温和着火预测的火焰蔓延建模相结合。“表面加热”意味着没有对深度反应进行建模,因此没有必要向模型提供实际的可燃质量,而燃烧材料(如电缆)的表面积参数就很重要。各托盘单位长度电缆的表面积是= 2 ,为电缆外径。在这项工作中,假设整个电缆表面,即2,可能(取决于火焰在托盘中蔓延的程度)暴露在高温和燃烧中。
正如上面提到的,这个单位长度表面积既不能平均分配在实际电缆数之间(因为在消防安全工程中,典型的CFD单元尺寸在5 - 10cm之间,是不允许的)也没有分配到一个水平板上(因为火焰的动力学在火焰传播方面是不同的)。这里使用的是四组电缆的中间数。每组电缆的尺寸不仅是要选择合适的表面积(单位长度),也是预选单元5cm值的倍数(这能够很好的解决本课题中火灾动力学的问题),从而使气相网格与代表电缆组的固体障碍物很好地对齐。基于此推理,如果每组电缆的矩形截面为0.10 m 0.15 m,则模型中每个托盘单位长度的表面积为(0.10 0.15)2 4 ㎡/m = 2 ㎡/m,对应于上述计算的实际值。这一选择,加上假设电缆组之间有5cm的间隙,导致模型托盘宽度为0.60 m,而实际托盘宽度为0.45 m。因此,预测的火焰可能比实验中更宽,这可能会影响视图因子,从而影响到潜在邻近物体的热辐射。但是,这方面超出了目前的研究范围。
或许有人认为电缆群的模型厚度会影响固相传热。我们将在稍后的文章中演示,对于目前的情况,电缆组是热厚的。因此,在传热计算中,代表电缆组的板的实际尺寸并不重要,只要它们在火灾过程中保持高于热穿透长度即可。
基于以上,本文考虑的火焰蔓延模型如下:首先,求解一维傅里叶方程(见方程2)及其边界条件方程3:
, (2)
, (3)
,c,和k分别表示燃烧材料的密度、比热和传导率(此处视为一个均质材料),T是固体的温度,t是时间, x是在材料内部的深入距离(即x = 0表示材料的表面)。变量和 分别表示固体表面的对流热通量和净辐射热通量。虽然电缆组是三维的,但一维方程2和3适用于其周长的四个边的法向,这是导热的优先方向。
然后,如果表面温度达到点火温度,则施加的单位面积热释放率(HRRPUA)剖面(作为时间的函数)为:
(4)
将HRRPUA与燃烧面积相乘,得到数值模拟计算的热释放速率。计算得到的火焰在固体(即电缆组)表面施加一定量的热流,该热流可用于计算公式3。
在这个阶段的主要问题是如何选择热物理性质,和k,以及和。
3.4.2 用锥形量热法估算燃烧材料的热物理性质
燃烧材料的热性能和表面点火温度从三个标准锥形量热法测试中估得,分别是两个在辐射热通量50 kW/㎡,和一个在60 kW/㎡辐射热通量(由Mangs和Hostikka,提供)下的试验。根据试样的着火时间推导出试样的性能。在50kW/㎡时,第一次试验为23秒,第二次26秒(重复性)试验。在60kW/㎡时,= 14秒。随后使用了两种方法。
方法一:
热厚固体(假设半无限行为)的着火时间可表示为:
(5)
其中和分别为表面着火温度和环境温度,为辐射热通量。
方程5可以改写如下:, (6)
是与极限条件= 0(即) 相对应的辐射热通量,是一个比例系数表达如下:
(7)
图2 按式6绘制的着火时间
根据圆锥量热法的数据,将式6绘制成图,如图2所示,绘制了两条线,两条线分别是基于60 kW/㎡时的= 14秒和50 kW/㎡时的两个值中的一个。相应的值(斜率)和 (即与x轴相交):
- 红线: ;
- 蓝线: ;

英语原文共 11 页
资料编号:[3541]
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


