RTK – GPS和全站仪在土地测量中的应用评估外文翻译资料

 2022-08-08 14:21:02

英语原文共 7 页，剩余内容已隐藏，支付完成后下载完整资料

RTK - GPS和全站仪在土地测量中的应用评估

1土耳其C.anakkale Onsekiz Mart大学Biga职业学校技术程序系，土耳其C.anakkale。

2北达科他州立大学迪金森研究推广中心，美国迪金森ND 58601。

电子邮件：unal1975 @ yahoo.com

在GIS环境下研究了实时运动全球定位（RTK-GPS）系统和全站仪（TS）的精度。在地统计评估中，将克里格方法与球面，指数和高斯模型一起使用。调查结果表明，用高斯模型可以最好地解释3.5公顷或更小的面积，而较大的面积则需要球形模型。当消除建筑区域以外的测量点时，可以观察到60 cm的垂直误差和30 cm的水平误差。 计算出每个调查点的最佳面积为20 ~20 m2，以提高准确性。此案例研究表明，不准确的调查可能导致成本超过估计值，最高可达27％。

关键词。 土地调查；RTK-GPS；全站仪；克里金；数据分析；仪器和技术。

1、引言

许多农业工程实践需要大量投资。因此，准确的成本估算对于项目的设计和施工至关重要。不正确的调查会导致形成不代表建筑区域的地形图。地形图也已用于划定子领域管理区（Fraisse等，2001）和特定地点的土壤管理（Franzen等，1998）。

实时运动学全球定位系统（RTK-GPS）是地形测量的组成部分。 RTK是一种在精度要求较高的实践中采用的技术。在RTK中，正确的 GPS信号从已知位置的基本接收器实时传输到一个或多个流动站接收器。随着基于RTK的GPS系统的最新发展，通过补偿GPS几何中的大气延迟，轨道误差和其他变量，可以实现1 cm的水平精度（Ehsani等，2004）。

Satalich和Ricketson（1998）报告说，与时间有关的系统误差可能会影响RTK-GPS系统的垂直精度。Clark和Lee（1998）使用RTK-GPS设备确定了场大小区域的地形。其仰角误差为4–9 cm。 Wilson等人（1998年）报告说，RTK-GPS在各个点上得到的仰角即使很小的差异，也可能导致诸如坡度梯度和集水面积等参数上的巨大 差异。

尽管成功应用RTK-GPS系统可以提高地形测量的质量，但在某些情况下，这些系统的准确性值得怀疑。任何自然或人为障碍物（例如树木和建筑物）的阻挡都可能使RTK系统使用受限或无法使用。在这种情况下，将使用全站仪（TS）。 Borgelt等人（1996年）将RTK-GPS系统与TS的准确性进行了比较。他们报告了12厘米的仰角误差。可以使用TS进行精确测量。但是，现场条件并不总是允许仪器的准确性。因此，这些系统在以下环境中一起使用土地调查。

使用诸如克里格（Kriging）等地统计方法 评估地形图的符合性 在时间方面进行第二次独立调查和成本。即使Kriging不提供作为第二次调查的最终答案，这是一个有效且廉价的技术（Barton等1999）。

为了说明地形调查数据的准确性，地克里格技术是克里格（Kriging）技术，用于创建预测图和空间统计信息。克里格（Kriging）是一种不同的思维方式预测性比使用确定性插值器进行的预测要好。在Kriging中，预测值取决于两个因素：趋势和附加要素变化性。例如，有上升趋势从较低的高度到顶部的高度一座山丘。但是，可能会有变化因为有山谷，溪流，旋钮和其他特征（ESRI 2006）。可能是因为这些变体，克里格（Kriging）会将权重分配给所有附近的点或称为“最近的邻居”的子集（Davis and Culhane 1984）。为了找到权重，关于空间依赖性的信息 调查点应该是已知的（Dowd 1984）。一种半方差可以用来表达这种空间依赖（Bras and Rodriguez-Iturbe 1985）。

半方差函数可以表示为：

gamma;（dij）= 12 var [（zi-zj）]，（1）

其中gamma;（dij）是点的半方差函数 Pi和Pj的标高为zi和zj，标高为 d的滞后距离。基于“内在假设”（Delhomme 1983），公式（1）可以写成：

gamma;（dij）= 12N N 1（zi-zj）2，（2）

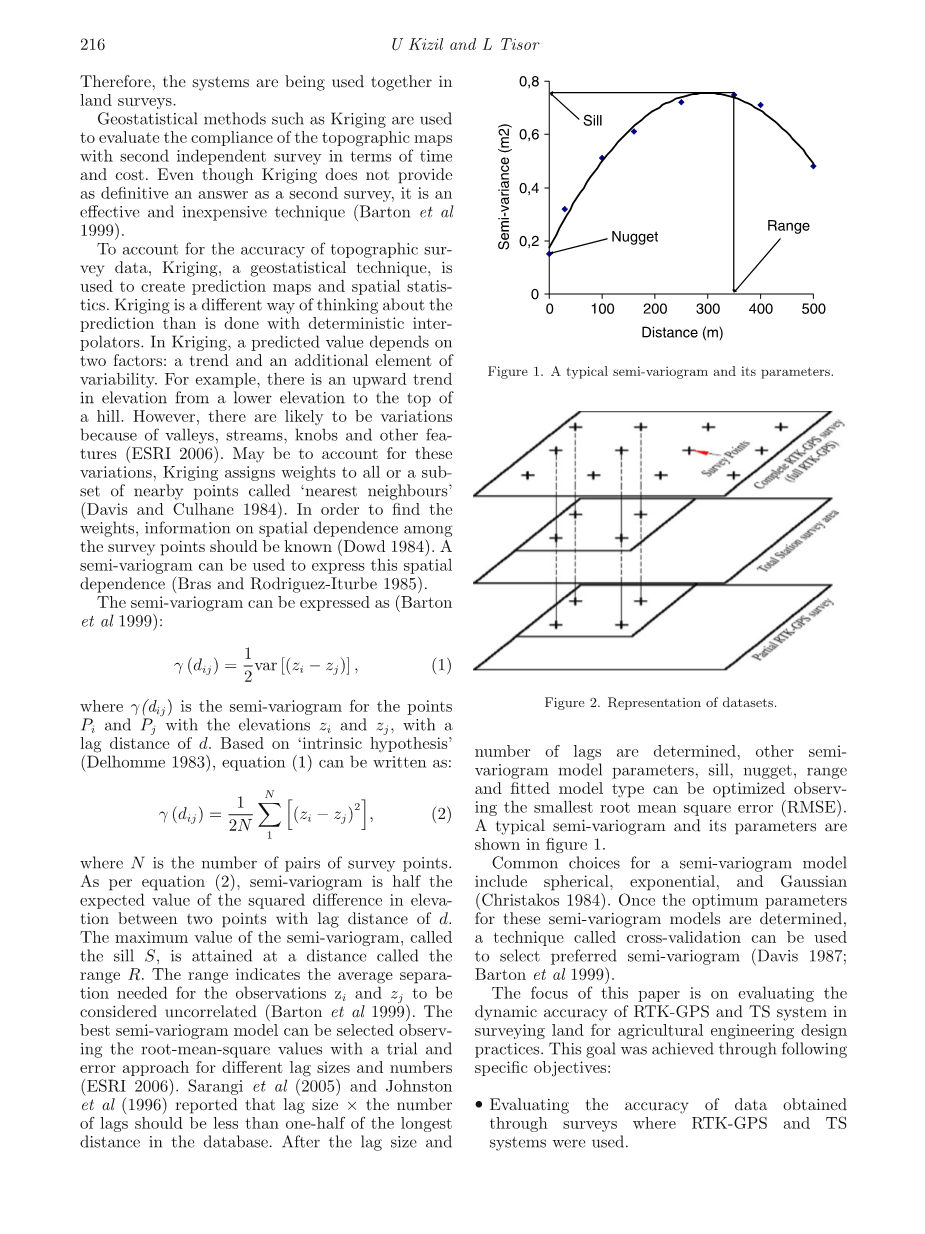
其中N是测量点对的数量。根据等式（2），半变异函数为一半滞后距离为d的两点之间的高度差的平方差的期望值。半变异函数的最大值称为窗台S到达的距离称为范围R。范围表示观测值zi和zj为被认为是不相关的（Barton等，1999）。这可以选择最佳的半方差模型，并通过试验观察均方根值不同延迟大小和数量的错误方法 （ESRI 2006）。Sarangi等人（2005）和Johnstonetal（1996）报道，滞后量times;数量滞后时间应小于最长滞后时间的二分之一数据库中的距离。确定滞后大小和滞后次数后，其他半方差数模型参数，门槛，块金，范围根据最小均方根误差（RMSE），可以优化和拟合模型类型。典型的半方差及其参数为如图1所示。

图1.典型的半方差及其参数。

半方差模型的常见选择包括球面，指数和高斯（克里斯塔科斯（Christakos）1984）。一旦最佳参数对于这些半方差模型，可以使用一种称为交叉验证的技术选择首选的半方差函数（Davis 1987; Barton et al 1999）。

本文的重点是评估实时RTK-GPS和TS系统的动态精度农业工程设计用地测量实践。这个目标是通过以下方式实现的具体目标：

bull;评估所获得数据的准确性通过RTK-GPS和TS的调查系统被使用。

bull;使用GIS和地统计方法来执行上述数据的质量分析。

bull;调查调查数据质量对工程设计。

2、材料与方法

2.1测试地点位置和数据收集

美国北达科他州Lefor附近的50公顷区域之所以被选为测试地点，是因为没有可以阻止的自然或人为障碍卫星信号。对该地区进行了调查 Trimble 5700 RTK-GPS（Trimble Navigation Ltd.加利福尼亚州桑尼维尔）的调查系统。基地站和四个参考点已建立在调查区域的最高点。调查点之间的距离为15 m。一个保持5-10 km / h的运行速度（Renschler et al 2002）拓扑模式。为了保持相等的距离在测量点线之间，手持式 Garmin GPSmap 76C（Garmin International Inc.，使用了堪萨斯州奥拉西（Olathe Kansas）的GPS装置。参照四个参考点，尼康NPL-350（尼康日本东京Geotecs Co.Ltd。全站仪经过现场校准以调查占地约3.5公顷。GPS勘测车轨道和手持GPS装置用于收集 TS读数尽可能接近RTK-GPS 调查点。

2.2数据处理。

可用的地形数据集最初是 存储为点测量。每个点都没有东西，东边和高程值。完成数据处理以创建等高线图用于设计Autodesk Land中的转移渠道Desktop 2006（加利福尼亚州弗里蒙特市的Autodesk）软件。在50公顷的土地上创建了三层 使用RTK-GPS系统进行了调查，面积为3.5公顷用于TS和RTK-GPS系统。现在开始，这些图层分别称为“完整GPS”，“ TS”和“局部GPS”（图2）。部分GPS数据将使我们能够观察数字的影响调查点对调查质量的影响。包含北，东，所有三层的每个点的高程已在AutoDesk中另存为数据库文件（dbf）。 然后，ArcGIS的Geostatistical Analyst扩展用于执行地统计分析。在经过分析，遵循了一个结构化的流程，如图3所示。

图2.数据集的表示形式。

添加图层并显示

调查数据集的统计属性

选择模型以创建曲面

评估输出表面

做出决定

图3.表面拟合方法。

最后，了解调查质量对工程设计，在三个方向上均具有4：1的边坡比的189 m净水分流通道数据集（图层）已创建。切割/填充计算 在AutoDesk软件中进行。

3。结果与讨论

产生最小RMSE的半方差函数用于球形，指数，高斯模型，以及交叉验证统计信息如表1所示。

表1.交叉验证错误统计信息。

M：平均误差； RMSE：均方根误差； ASE：平均标准误； MSE：平均标准错误； RMSSE：均方根标准化误差。

交叉验证给出了“效果如何”的概念 该模型可预测曲面创建中的未知值。在交叉验证中，模型顺序省略一个点，使用以下方法预测其值 其余数据，然后比较预测的和观察值。在最佳模型中，均值误差应接近于零；RMS和平均年龄标准误差应尽可能小。获得最小的RMSE值使用球形模型进行RTK-GPS测量（Goovaerts 2000）。交叉验证表还显示面积的大小和读数的数量可以导致不同的半变异函数模型。甚至 尽管所有三个阅读间隔都相同调查中，完整的RTK-GPS调查数据由 球形模型，而其他模型则需要高斯模型。

图4显示了局部之间的区别以及完整的RTK-GPS调查。部分轮廓图 在较小的区域中使用相同的测量点，导致水平误差最大为30 cm，并且使用RMSE 为0.7904，而相同的数字表示全轮廓地图是0.4144。分析表明，越大读数越多的区域，质量越好地图。

图4.完整和部分RTK-GPS等高线图

还发现较少的调查点和较小的面积会产生重大影响在垂直精度上。净水分流通道的轮廓代表了垂直精度三个调查数据（图5和图6）。

TS和局部RTK-GPS地图产生了类似的结果，因为调查点数相同和区域，如预期的那样。垂直差异在5 50站的全面和部分测量之间高达60厘米。

图5.干净的引水通道布局

图6.净水引水渠剖面

减少三个渠道的数量在部分和完整的RTK-GPS上进行设计，并且 计算了TS等高线图（图7）。考虑到完整的RTK-GPS调查是最准确的一种，切割误差分别为140和393 m3 分别用于部分RTK-GPS和TS勘测是重要的。北达科他州的开挖统一费率为1.2美元/立方米（ND-NSPMP 2005）。 因此，在切割量计算中出现393 m3的误差可能会导致189 m的成本差471美元（27％）渠道。为了进一步观察数字效果切割量的调查点数，不同数量计算得出的体积（图8）。选择了33、62、80、100和162个数字用于局部调查区域。整个调查区域最初有749个调查点，总砍伐量为1460 m3。作为调查点数减少，切割量增加。50公顷的749个测量点之间的削减体积差异在3.5公顷的面积上有100个测量点可忽略不计。因此，每3.5公顷的面积有100个测量点，或读数之间的20 m距离产生合理结果。

图7.部分完整的RTK-GPS的频道剪切量和TS地图。

调查点数

图8.调查点数量与减少音量。

4.结论

使用调查数据来创建准确的地形表现必须非常小心，因为这对任何农业都至关重要工程设计。地统计分析是进行调查以查看调查区域的大小和读数数量是否对半变异函数有任何影响模型。此外，它的目的是观察调查准确性对工程设计质量和成本估算的影响。不同地区 读数的大小和数量显示出很大的不同结果。

bull;两种技术的比较，包括 RTK-GPS和TS透露基于RTK-GPS的调查不仅实用，快速，而且还可以产生更准确的地形图设计目的。因此，在 RTK-GPS系统可能值得。

bull;即使所有调查都是针对同一地区，解释了50公顷的RTK-GPS调查与球面半变异函数模型同时其他人使用高斯模型。因此，对于成功的调查之一不应该限制区域只能到建筑工地。更大的区域增加调查的质量。

bull;测量技术，面积和之间的距离勘测点可能会导致垂直误差，最高可达 60厘米之间可能会产生巨大差异的成本估算和实际成本。

bull;两次之间的最佳读取间隔为20 m 可以使用调查点来提高质量 工作。

参考文献

Barton J M H、Buchberger S G和Lange M J1999Kriging调查中的误差和遵从性估计；J.Surv。 英格。 125（2）87–108.

Borgelt S C，Harrison J D，Sudduth K A和Birrell S J1996GPS在精密农业中的应用评价；APPL。 英格。 农业。 12（6）633–638.

Bras R L and Rodriguez-Iturbe I1985Random function and Hydrology(Reading，Mass。 *Addison Wesley)，pp。 359–425.

克里斯塔科斯G1984关于允许协方差和变分模型的问题。 决议。 20（2）251–265.

克拉克·RL和李·R1998年用运动GPS精确农业地形图的开发。 Asae41（4）909-916。

地质统计学中交叉验证的使用和滥用；数学。 乔治。 19（3）241–248.

戴维斯·M·W和库尔汉·P·G1984利用克里金绘制非常大的数据集；自然资源表征的地理统计，第2部分。 (Dordrecht，The Netherlands：Reidel)，pp。 599–619.

Delhomme J P1983Kriging in the hydrosciences；In：Flow through Porous Media(ed。) G P Findler，pp。 99–113.

198

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[257576]，资料为PDF文档或Word文档，PDF文档可免费转换为Word

原文和译文剩余内容已隐藏，您需要先支付 30元 才能查看原文和译文全部内容！立即支付

以上是毕业论文外文翻译，课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。

您可能感兴趣的文章