
英语原文共 13 页,剩余内容已隐藏,支付完成后下载完整资料
模型预测控制—— 一个简单而强大的功率变换器的控制方法
Samir Koura,IEEE会员,Patricio Corteacute;s,IEEE会员,Reneacute; Vargas,学生会员IEEE,IEEE会员Ulrich Amman和IEEE高级会员Joseacute; Rodriacute;guez
摘要-本文详细描述了应用于功率变换器的有限控制集模型预测控制(FCS-MPC)。深入地介绍了与这种方法相关的几个关键方面,并与传统的功率转换器控制技术(例如基于脉宽调制的方法的线性控制器)进行了比较。其中基本概念,操作原理,控制图和结果用于比较不同的控制策略。该分析是在传统的三相电压源逆变器上进行的,用于作简单而全面的参考框架。而其他拓扑和电源系统的重点在于突出FCS-MPC的差异性,潜在性和挑战性。其中的结论是对于当前的信号处理能力,尤其是对于开关状态数量减少和操作原理更复杂的电力系统(如矩阵转换器)而言,FCS-MPC具有可行性和巨大潜力。此外,通过单一成本函数轻松解决不同或额外控制目标的问题的功能,可为功率转换系统提供简单,灵活且性能优异的控制器。
关键词:可调速驱动器;电流控制模型预测控制(MPC);电源转换器;脉宽调制(PWM)
引言
自20世纪下半叶以来,功率变频器和驱动控制技术一直处于持续发展中,并已被证明几乎在所有应用领域(能源,通信,医药,采矿,运输等)都具有实用技术。特别是,转换器控制技术一直是电力电子领域的一个非常活跃的研究课题,涵盖了无数的低、中、高功率应用拓扑结构[1]-[4]。传统线性控制器和基于迟滞比较器的非线性控制器一直是功率转换器中分析和开发最广泛的控制策略[2]。这可以通过最初由施加了限制的控制回路的模拟实现来解释。这些控制方法后来适用于离散时间数字实现,且这些实现目前被广泛视为行业标准。
另一方面,数字信号处理在过去的几十年中经历了更加爆炸式的发展,从而实现了新兴的并且通常更复杂的控制技术。其中一些方法已经应用于功率变换器,其中包括模糊[5]-[6],自适应[7]-[8],滑动模式[9]-[10]和预测控制。后者是一个广泛的控制概念,可以根据工作原理和其他特征进一步细分或分为几类[11]。一般而言,预测控制可以被认为是使用系统模型预测其未来行为的任何算法,并基于最优性标准选择最合适的控制动作。早期用于电源转换器的预测控制器之一就是所谓的死区控制,这通过使用系统的预测模型消除了经典的线性控制器。该模型用于计算所需的参考电压,以便达到某个变量(通常是电流)的所需参考值。预测的参考电压稍后由转换器经由调制级产生。该方案已应用于逆变器[12]-[19],整流器[20]-[21],有源滤波器[22]-[23]和不间断电源(UPS)[24]-[25] 。
一种不同的方法是模型预测控制(MPC)[26],其中考虑系统的模型以预测变量在一定时间范围内(整数倍采样时间)的未来行为。这些预测基于成本函数进行评估,然后选择使成本函数最小化的序列,以这种方式获得未来的控制行为。它是只应用序列的第一个值,并在每个采样周期再次计算的算法。MPC有几个优点,例如容易包含非线性和约束。由于需要大量的计算来解决在线优化问题,这种方案在电力变换器控制和驱动中的应用很少,这与用于转换器控制的小采样时间不相容。为了减少计算时间,一种解决方案是解决流程优化问题,如文献[27]中所述,其中MPC被实现为搜索树并且计算时间减少,使得可以在驱动中使用MPC控制。另一种解决方案是使用广义预测控制(GPC)[28],该方法通过优化分析获得一个线性控制器。不过,该方法对于包含系统约束的GPC和非线性的情况非常困难。
用于实现功率变换器和驱动器的MPC的另一种方法是利用功率变换器固有的离散特性。由于功率转换器具有有限数量的开关状态,MPC优化问题可以简化为仅针对可能的开关状态预测系统行为。然后,每个预测用于评估成本函数(也称为质量或决策函数),从而选择并生成成本最小的状态。这种方法被称为有限控制集MPC(FCS-MPC),因为可能的控制动作(开关状态)是有限的。这种方法也被称为有限字母MPC或简称为预测控制,并已成功应用于广泛的功率转换器和驱动应用[29]-[56]。在本文中,介绍了功率变换器和驱动器的FCS-MPC的一般方法。本文的部分内容是调查性质,是针对该技术的最新进展和前景。此外,还介绍了FCS-MPC和经典线性控制器的比较。特别注意工作原理,控制器设计和实现的概念差异。传统的两电平电压源逆变器(2L-VSI)已被选为主要拓扑进行比较。原因是其更通用的结构,简单的工作原理和工业存在。此外,这种拓扑结构对于两种控制技术来说都是中性的,这意味着它没有特殊的特征或有利的特征,使得一种方法胜过另一种方法,从而为分析提供了一个公平的参考框架。此外,其他转换器拓扑结构,驱动器和应用程序也可用于展示FCS-MPC的灵活性和潜力。
FCS——MPC操作原则
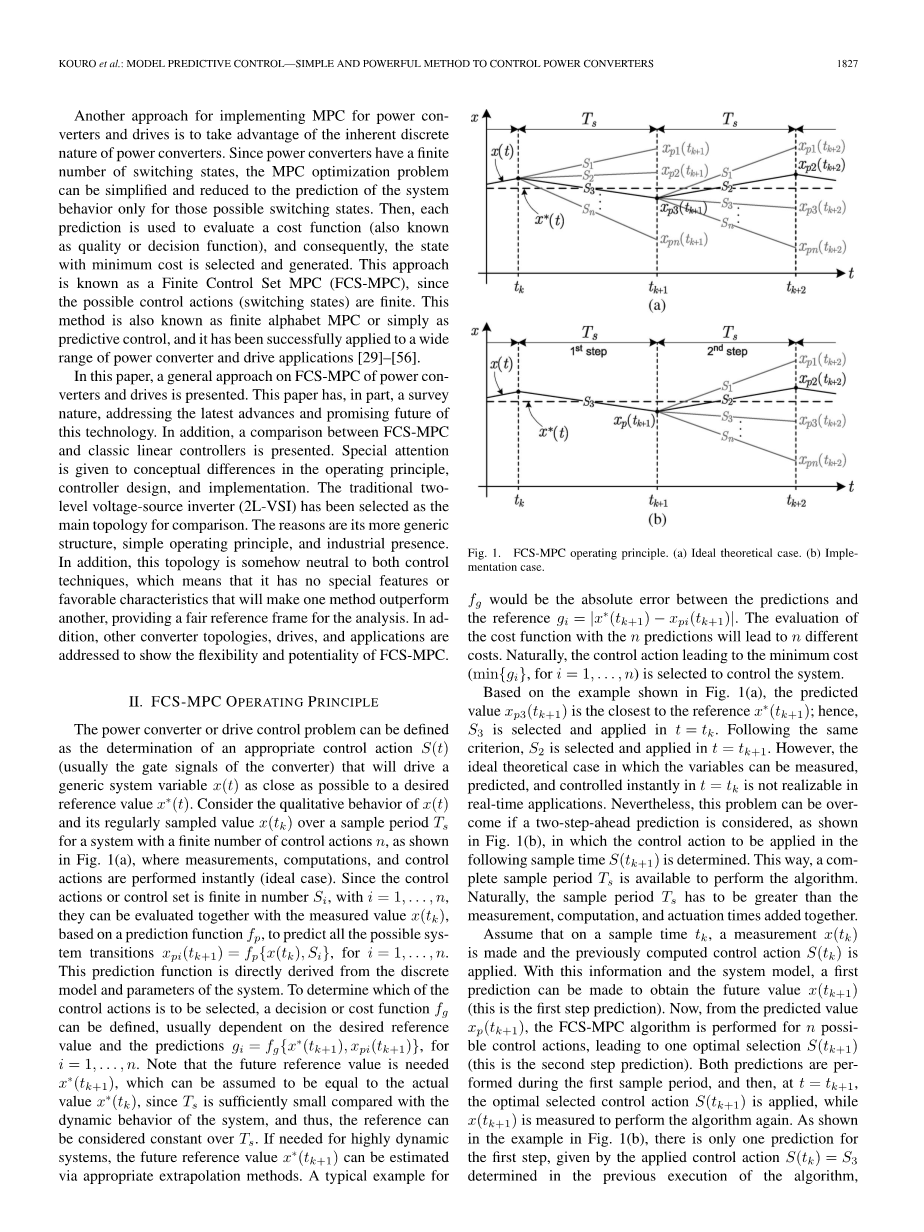
功率转换器或驱动器控制问题可以被定义为确定适当的控制动作(通常是转换器的门信号),其将通用系统变量尽可能地接近期望的参考值。如图1(a)所示,考虑具有有限控制行为数量n的系统在采样周期内的及其定期采样值的定性行为,其中测量、计算、并立即执行控制动作(理想状况)。由于控制行为或控制集合是有限数量,其中= 1,...,n,它们可以与测量值一起根据预测函数进行评估,以预测所有可能的系统转换,对于 = 1,...,n。该预测函数直接从系统的离散模型和参数导出。确定哪些控制行为将被选择,决策或成本函数可以被定义,通常取决于期望的参考值和预测,对于ⅰ= 1,...,n。请注意,未来的参考值需要,可以假定它等于实际值,因为与系统的动态行为相比,足够小,因此,该参考可以被认为是在上不变。如果高度动态系统需要,可以通过适当的外推方法估计未来参考值。一个典型的例子将是预测与参考值之间的绝对误差。用n个预测评估成本函数将导致n个不同的成本。当然,选择导致最低成本(,对于ⅰ= 1,...,n)的控制动作来控制系统。
图1. FCS-MPC的工作原理
(a)理想的理论情况 (b)实施案例
基于图1(a)所示的例子,预测值与参考)最接近; 因此,被选择并应用于。遵循相同的标准,被选择并应用于。然而,理想的理论情况下,变量可以在内即时测量,预测和控制,在实时应用中无法实现。然而,如果考虑到两步超前预测,如图1(b)所示,在后面的采样时间中要应用的控制动作是决心。这样,完整的采样周期可用于执行该算法。当然,采样周期必须大于测量值,计算值和加速时间。假定在采样时间,测量并且应用先前计算的控制动作。利用这些信息和系统模型,可以进行第一次预测以获得未来值(这是第一步预测)。现在,根据预测值,对于n个可能的控制动作执行FCS-MPC算法,导致一个最优选择(这是第二步预测)。这两种预测都是在第一个采样周期内完成的,然后,在时,应用最优选定的控制动作,而测量以再次执行算法。如图1(b)中的例子所示,对于第一步只有一个预测,由前面执行算法中确定的应用控制动作给出,而从第二步的n个预测中选择。
图2. FCS-MPC通用控制
图3. FCS-MPC通用算法
一个简化的控制框图和实时实现FCS-MPC的相应算法如图1和图2所示。考虑一个通用系统变量,分别为2和3。值得一提的是,这种控制方法并不局限于单个变量; 相反,多元变量、系统约束、扰动、饱和度以及基本上可以数学建模和测量的每个特性都可以包含在预测模型和成本函数中。这是FCS-MPC可以实现巨大灵活性和控制潜力的基础。此外,电源转换器具有减少且有限数量的开关状态(或控制组)的问题可用现有的微处理资源来实现。由于只需要系统的离散模型,而不是近似线性模型以及控制系统设计理论和调制算法,因此可以实现控制器的更简单和更直接的设计和实施。
经典线性PI与FCS—MPC的比较
为了突出传统控制方法的FCS-MPC方法的概念差异,本节将介绍2L-VSI的当前控制的比较。2L-VSI由于是业内最广泛的转换器拓扑之一而被选中,有通用结构和工作原理,可轻松扩展到其他转换器拓扑结构。
图4. VSI电源电路
电源转换器概述
2L-VSI的电源电路如图4所示。为简单起见,假定无源二极管前端整流器提供直流母线电压。该转换器由三相支路组成,可通过控制和的支路的两个电源开关,将相应的负载端子连接到转换器的正(P)或负(N)。由于有三个阶段,每个阶段具有两个控制动作,所以有个不同的开关状态。如果电压空间矢量被定义为
(1)
其中; 然后,评估不同的开关状态,转换器可以产生8个电压空间矢量(,...,),如图5所示。为进行比较,考虑了线性电阻电感RL负载。
具有2L-VSI的空间矢量调制(SVM)的线性PI电流控制
VSI的传统电流控制由两个阶段组成,一个是线性比例积分(PI)控制器,后跟一个调制阶段,通常是脉宽调制(PWM)或SVM [2]。对于PI控制器设计,转换器是忽略,并且从RL获得传递函数的负载模型。
图5. VSI电压空间矢量,开关状态和成本函数依赖
(2)
其中L是拉普拉斯变换。PI控制器传递函数是
(3)
其中和分别是比例和积分参数,可以通过极点配置或根轨迹程序[57]设计。两个PI控制器是必要的,一个用于,另一个用于或的ⅰ分量和组件(如果考虑旋转框架)(取决于应用程序)。控制器的输出是校正当前轨迹所必需的电压矢量。该参考电压矢量然后由PWM或SVM [2]转换器调制。特别是不连续SVM已成为调制阶段的标准方法[58]。该方法的简化控制图如表一所示。请注意,对于所选示例,负载是线性的; 因此,其模型和相应的控制没有更多的复杂性。然而,转换器具有饱和(最大电压和电流),这是非线性条件,通常可以通过抗风险算法来克服。其他转换器,负载以及特别是电动机驱动器是高度非线性的系统,这使得控制器设计的近似线性化传递函数的获得变得复杂,从而导致稳健性问题。此外,在当今数字平台中实施PI控制器需要控制器的离散化。此外,忽略设计过程中保持的转换器假设只有在实现高带宽调制阶段时才有效,这对于高开关频率是正确的,因此导致更高的损耗并需要更多的数字处理能力。一个有利的特征是基于PWM或SVM的调制级施加固定的平均开关频率。
2L-VSI的电流FCS-MPC
FCS-MPC电流控制问题很容易从第二节分析的一般工作原理中推导出来。变量将是当前的; 控制动作表示图5所示转换器的开关状态(,其中ⅰ= 0,...,7)。预测模型对应于负载的离散时间模型,其中a欧拉近似导出的电流导数
(4)
(5)
是测量电流,是由开关状态产生的电压矢量,其中ⅰ= 0,...,7。另外,注意。最后,需要最小化的成本函数是
(6)
当前FCS-MPC的相应简化框图如表1所示。
表1. 在传统线性控制器(包括调节)和FCS-MPC中进行比较
为了进一步说明算法的工作原理,图6(a)和(b)分别显示了时间和空间矢量表示中的系统行为。阴影区域对应于两步电流预测,如前面图1(b)所示。注意,现在,两个变量由一个成本函数(6)控制。从空间矢量波形可以清楚地认识到,一些向量对在alpha;分量上产生相同的效果; 例如,和产生的增加,而和产生减少。另外,和分别产生更高的增加和更高的减少。例如,这解释了为什么在时间表示中,高于所有其他当前预测。正如预期的那样,零矢量和并没有改变我的全部。以类似的方式,增加和,由和减小,并且通过,和,和保持相等。
基于图6(a)中所示的预测,对于,选择的向量是和,而对于,选择的向量是和因此,满足这两个条件的总体选择是,这可以清楚地理解为图6(b)中的最佳选择。
图6. FCS-MPC电流控制工作原理
(a)时间表示和控制 (b)控制的空间矢量表示
虽然在这个说明性示例中不能直接观察到,但FCS-MPC不会在每个采样周期强制换向。因此,平均开关频率是可变的,导致扩展电流频谱。然而,这个缺点可以很容易地得到补偿,这将在后面讨论。表1给出了两种分析方法的最显着特点的总结。在相同的操作条件下,两种情况下均可得到表中所示负载电流动态特性的仿真结果。这些结果是使用Matlab / Simulink获得的,具有=100mu;s的样本时间。在t = 0.035s时改变步伐,仅在13至2.6A的电流的alpha;分量上执行。在这种情况下,这两种方法似乎表现相当。然而,alpha;分量中的步骤对为了带有支持向量机控制算法PI的beta;分量有耦合影响,而在FCS—MPC中,没有出现这种效果。
对此主题进行深入的比较和评估在文献[59]中介绍。
成本函数灵活性和潜力
带调制的传统线性控制器受到到他们经典的反馈结构的限制。而且,带宽和控制器的鲁棒性将取决于控制器的优势系统的非线性。另一方面,FCS-MPC,使用系统的完整预测模型和反馈包含在成本函数中,不限于此受控变量的误差的大小,如分析中的第三部分的例子。事实上,它具有诸如错误可以被测量此类的功能。
(7)
(8)
(9)
(7)和(8)之间的区别在于后者产生了过度比例的成本(两倍的力),与较小的成本相比,对较大的错误产生较高的惩罚。这可以用来控制更接近参考的变量并减少波纹幅度。实质上
全文共15245字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[14133],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


