
英语原文共 8 页,剩余内容已隐藏,支付完成后下载完整资料
用动态规划的配电系统的最优恢复
Rauacute;l Peacute;rez-Guerrero, Student Member, IEEE, Gerald Thomas Heydt, Fellow, IEEE, Nevida J. Jack, Brian K. Keel, Member, IEEE, and Armindo R. (Cas) Castelhano, Jr.
摘要:本文利用状态约简的动态规划方法解决了配电系统的恢复问题。该算法是一种操作员许可的自动化方法,用于在停电后恢复配电系统。动态编程公式中的状态代表了馈线供电的时间和选择。增强型动态编程方法通过对彼此靠近的状态进行分组并选择最佳状态来减少状态数量。该算法在8个馈线/ 32负载分配系统上进行测试。该方法适用于径向配置的系统。
关键词:配电自动化,配电系统,动态规划(dynamic programming,DP),服务恢复
引言
电力系统运行的一个基本任务是停电后的恢复,恢复过程会在系统组件因停电而丢失任何联系后使系统恢复正常运行。恢复传统上是由配电系统操作者执行的,配电系统操作员通过公用事业公司制定的指导方针使用经验积累的知识进行辅助[1]。
用于简化这一任务的常用方法是将恢复过程分成几个阶段。 刘等人建议基于当前操作员的目标提出三个阶段[2]:准备,系统恢复和负载恢复。前两个阶段分别处理系统配置的评估和主传输电网的恢复,负载恢复阶段的重点是通过逐渐重新激活配电系统的所有馈线来最大限度地减少停电的影响。
即使恢复一直是输配电工程中的一个重要课题,但近年来,配电网的恢复越来越受到重视。对配电恢复越来越重视的部分原因是配电自动化的进展和与电力市场营销和开放售电有关的最新做法,特别是自动化有可能改进恢复过程并减少中断的持续时间。此外,自动化或许能帮助减少恢复过程中的操作者错误。
配电系统恢复问题对操作者提出了若干挑战,其中许多来自系统的大部分维度以及涉及的多个操作决策变量。例如,一个分配系统操作员处理一个大系统的恢复可能面临许多配电线路的几乎同时恢复。在许多情况下,恢复过程的指导方针可能难以适用于全系统,或者由于恢复问题的大解空间而导致次优结果,这是由于恢复问题的组合性质和所使用的模型中经常需要的详细细节。
配电系统恢复,即服务恢复,过去受到了研究人员的广泛关注。大部分是操作者结合分析工具分发恢复计划,恢复计划协助操作者进行决策过程并改善恢复任务。为了实现这一点,一些基于知识的方法已经被提出,其中包括专家系统[ 3 ] [ 6 ]、人工神经网络[ 7 ]和启发式[ 8 ] [ 11 ]方法的使用。这些方法具有潜在的吸引力,因为它们具有模拟系统操作员的能力。然而,这些技术的一个潜在缺点可能是执行任务所需的信息量,尤其是在大型系统中[ 12 ];还有一个缺点是所使用的训练集可能无法捕捉所有的突出现象需要准确的解决方案。也提出了由更传统的优化工具驱动的工具,最值得注意的是包括内点[13],基于排序的方法[14]和结合混合模糊集技术的混合整数规划[15]的使用。这些方法依靠适当的模型和近似优化恢复过程。但是,不准确的模型可能不会导致问题的全局最优解;另外,模型的精度与算法性能有关,而算法性能在恢复过程中可能至关重要。
基于知识的配电系统恢复问题的解决方案基本上是基于故障或其他局部扰动后恢复的假设;这些恢复概念往往假定局部系统信息可用,而主配电线路可能在几个点上通电。本文探讨了配电系统的恢复过程,假设完全径向配置,并假设广泛停电,而不是本地中断的服务。传统的变电站和径向配电系统配置被假定,分布恢复过程的基础是一种增强的动态规划算法。动态规划(Dynamic Programming,DP)是基于贝尔曼的最优原理[ 16 ],文献[ 17 -18 ]是对方法的文档抽样。DP是一种用于系统地评估业务策略稳健的优化工具,为了解决DP的维数问题,采用状态缩减技术来缓解恢复问题。该算法为服务恢复找到一个逐步的顺序,以减少停电对服务交付点的影响。
配电系统恢复
配电系统恢复可以定义为主配电系统停电重新供电的过程。图1是对恢复过程的概念描述(基于文献[2]的理论),此恢复过程可以表示为一个在可用的生成、系统频率和负载优先级的约束下的优化问题。一般最优分布恢复问题可以表述为
(1)
约束条件为:
(2)
(3)
其中,表示恢复问题的目标函数;和分别是系统的等式和不等式约束集;是问题的决策变量集。
图1 恢复过程组成
1)目标函数
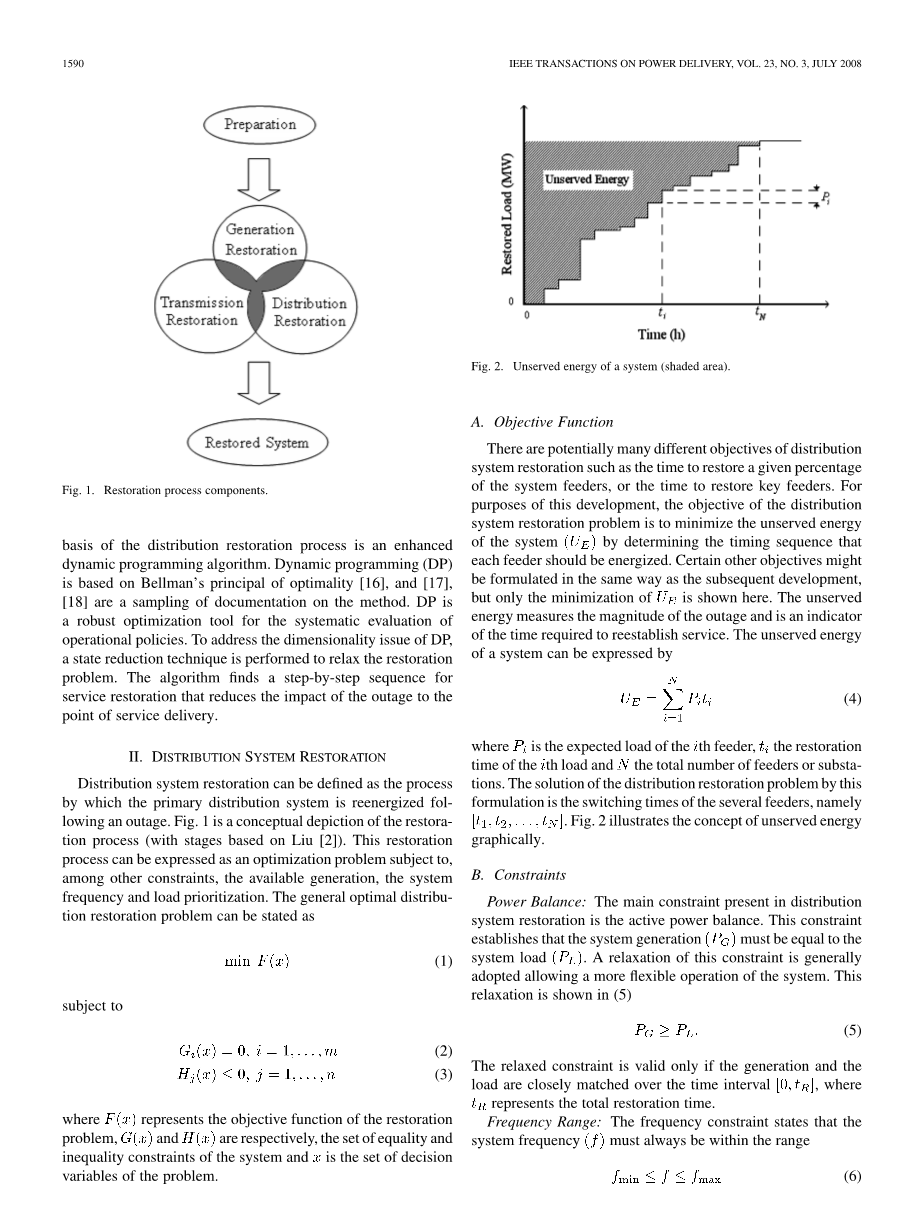
配电系统恢复可能有许多不同的目标,例如恢复给定系统馈线的百分比的时间,或恢复密钥馈线的时间。为了这个发展目的,配电系统恢复问题的目标是通过确定每个馈线应该被激励的时序来使系统的无功最小;某些其他目标可能会与后续开发的方式相同,但这里只显示最小化。没有能量的能量衡量停电的大小,并且是重建服务所需时间的指标。 一个系统的无功可以用下式表示
(4)
其中,是第馈线的预期负荷,恢复了第负荷的恢复时间和馈线或变电站的总数。用此公式求解分布恢复问题的方法是几种馈线的切换时间,即。图2是缺电的概念图形。
图2 一个系统的缺电图形(阴影区)
2)约束条件
(1)功率平衡:配电系统恢复中的主要制约因素是有功功率平衡。此约束规定系统生成的有功功率必须等于系统负载消耗的有功功率,通常这种放宽的约束条件应用允许系统更灵活地运行。其条件为
(5)
只有当生成的有功功率和负载消耗的有功功率是紧密匹配的时间间隔时,此约束条件是有效的,其中代表的总恢复时间。
(2)频率范围:频率约束状态,系统频率必须始终在范围内
(6)
其中和分别是系统允许的最小和最大频率。
为了避免大的频率偏差,一些电力公司将负荷回升限制在同步发电的5%。操作实践表明,这种负载拾取的百分比通常会导致大约0.5赫兹的频率降低[1]。
- 优先级排序
优先级别排序是根据重要性确定哪些负荷馈线应优先供电,这种优先顺序是恢复过程中的常见做法,医院、机场、警察局和污水处理厂的优先供电是典型例子。
状态缩减的动态规划
DP是理查德·贝尔曼于1950年代开发的一种优化技术[16]。DP是将问题分解为几个阶段(或子问题)并优化这些子问题的解决方案,解决这一问题的最佳方法是最佳策略组合。DP对比其他优化技术的几个优势种最值得注意的是它的能找到全局最优解。此外,由于DP不是基于微分的方法,所以它能够解决非连续解空间的问题,例如整数或离散变量的情况[ 17 ]。DP的一个主要缺点是当决策变量的数目很高时计算量很大,这个问题被称为维数灾难[ 16 ]。
为了解决维数灾难,许多策略和变化的DP已经制定出来。最初通过结合拉格朗日乘子[ 19 ],逐次逼近[ 20 ]和多项式逼近[ 21 ]来增强DP;此外还提出了其他方法,如分支定界技术[ 22 -23 ],插值和外推方案[ 24 ]和特殊分区[ 25 ];rsquo;最近的方法将DP与学习和并行实现相结合,如神经DP [ 26 ]和近似DP技术[ 27 ]。
在优化过程中,某一特定阶段的某些状态可能彼此“接近”,这种接近允许这些状态从优化过程中移除,从而加快了计算速度,这种方法称为分组降维(或者称为凝聚算法)。凝聚算法能识别并分类,并选择性能最佳的状态,邻近而冗余的状态在优化过程中被丢弃。状态约简(也称为聚合),通过解决原问题的松弛提高了DP的性能,但由于问题的解决是一个近似,因此不能保证问题的全局最优解。一些人可能被认为是状态聚集技术的引进者:Hinderer [28],Morin [29],Axsauml;ter [30] ,Bean、Birge 和Smith [31]等将状态聚合技术应用到DP。最近的状态聚合技术的应用出现在文献[ 32 - 33 ]。
基于DP的恢复算法
DP可以用来寻找配电系统的最优恢复方案,这个最优方案决定恢复的顺序,最大限度地减少了系统的缺电。这种优化过程受到功率平衡约束和频率偏差限制,馈线被建模为没有动力学的阶跃函数。
DP算法将恢复问题划分在恢复过程中要采取的步骤的几个阶段。每个阶段都由代表馈线所有可能组合的状态组成。阶段间通过弧线连接,每条弧线表示需要在恢复过程中从k级到k 1级的馈电线路,此过程如图3所示。
图3 动态规划(DP)的优化组件
DP执行两个主要功能来优化问题:其一是从现有的所有可能路径中找到最佳路径,这是在每个阶段为每个状态所做的;二是浏览整个优化过程,直到找出路径的组合从而找到最佳的解决方案。
1) 约束建模
(1)频率偏差:频率偏差是基于0.5赫兹的频率减少规则来计算的[1],不能满足这些标准的国家在特定阶段被取消审议。为了加快算法的速度,这个约束的预处理是可能的。由于配电系统的恢复发生在某些一代已经同步之后,在进行优化过程之前,可以对整套馈线进行筛选以满足其要求。
- 功率平衡约束:通过确定某一特定状态(或馈线组合)与预期可用生成曲线相匹配的时间来满足此约束,这样可以确保所有测试的组合都满足功率平衡等式约束,而不满足该约束的馈线组合在该过程中被淘汰。
- 优先级排序恢复
在用优先级排序算法进行配电系统恢复时,馈线按等级分类。恢复算法是对每一组馈线按从最高优先级开始并接着到更低组的顺序依次运行直到所有组的顺序得到优化,在每一组优化的基础上,最大限度地减少缺电(4)。需注意的是,首先恢复高优先级馈线,接着恢复优先级较低的馈线,再接着恢复更低优先级的馈线,并按此顺序接着恢复。
在优化过程中,由于生成曲线是一个固定的输入,因此在优化各组顺序时必须对其进行调整。通过减去期望的一代,即在优化某个组之前已经恢复的总负载来进行调整。
- 状态约简
状态约简是在基本DP算法中添加的一个附加过程,此过程在对应状态计算之后的每个阶段执行。状态约简将那些可以被视为“密切”的状态以加速优化进程为目的,实际上,随着解决方案的进展,解决方案的分辨率(即精度)提高了,该算法如图4所示。
图4 基本函数的状态简化流程图
使用用户定义参数构造组,在生成一个阶段的状态之后,将它们从最小到最大排序,与相应的恢复功率量排序。然后,算法通过添加第一个状态(最小功率恢复)用户定义的参数来创建组。在组范围内的所有状态都是集群的,选择性能更好的状态代表在剩余优化过程中的组。该算法选择不属于组内的下一个状态,并重复集群和选择过程。这些步骤中的每一个如图4所示。
聚类的有效性取决于组的大小,大组的大小将消除大量的状态,从而导致更快的算法性能,小组规模产生更精确的解决方案。
- 恢复的基础设施
这种增强的基于DP的恢复算法每隔几分钟执行一次,与分布恢复过程并行,此同步计算应向操作员提供一组可用于还原系统的选项。该算法是允许类型,目的是在恢复过程中与操作者不断地交互。然而,决策仍然由操作者根据一些标准和个人经验来执行。
交互是首先根据系统条件的初始估计创建总体计划,随着配电系统的恢复和对总计划的调整,算法必须根据系统剩余部分更新计划,这个概念如图5所示。实线表示DP恢复算法返回的原始恢复计划,黑色菱形和白色圆圈为标志的线条代表了不同的修复计划,这些计划需要和分别考虑到原始修复计划的偏差。
图5 以DP算法为指导的配电系统恢复
算法性能随系统(或岛)尺寸而变化,然而,一般的计算时间位于所谓的操作实时。操作实时的通用时间帧是以秒到几分钟的顺序,图6示出了电力系统中操作实时性的概念图。特别要注意的是恢复计划的准确性是作为输入数据的负载和生成估计的函数。
图6 电力系统的时间框图
算例分析
用例子I、II和III说明所描述的概念,在8馈线/ 32负荷系统用基于DP的恢复算法对所有例子进行了测试。开发的所有示例都考虑连接到同一电源总线上的所有馈线,图7示出了正在考虑的配电系统的单线图,附录列出了测试系统馈线上的估计有功功率,这些是从停电前测量的有功功率并乘以一个占冷负荷拾取的因素得到的[ 34 ]。在这项研究中,期望的发电数据(即变电站在时间上的可用生成)在配电恢复过程中被认为是已知的。
图7 (a)8 feeder-32负荷配电系统单线图的算例说明;(b)显示在每个例子中的馈线的详细成分
所有的恢复的算例都是基于缺电最小化。算例I评估了建议的增强DP算法,并与传统DP算法进行了比
全文共13069字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[12438],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


