英语原文共 9 页,剩余内容已隐藏,支付完成后下载完整资料
用于精确计算低频瞬态的实验验证的可逆单相多绕组变压器模型
IEEE会员Saeed Jazebi和IEEE高级会员Francisco deLeoacute;n
摘要 - 在本文中,先前公布的用于表示多绕组变压器漏感的模型得到了增强,以支持精确计算低频瞬变,包括涌流,串联铁磁谐振和地磁感应电流。 新电路是从二元性原理中获得的,因此在物理上是一致的。 改进模型的独特之处在于,在不改变参数的情况下,为每个绕组同时适当地表示铁芯的非常深的饱和行为(可逆模型)。 磁滞周期和铁芯损耗也包括在内。 除了其可逆终端行为以及物理一致性之外,所提出的模型还可以用电磁暂态程序类型程序中的电路元件构建,并且所有参数都可以从终端测试中计算出来。 通过比较三绕组和四绕组变压器的计算机模拟与实验室测量,验证了该模型。
关键词 - 对偶,电磁瞬变,铁磁谐振,地磁感应电流(GIC),涌流,多绕组变压器。
- 介绍
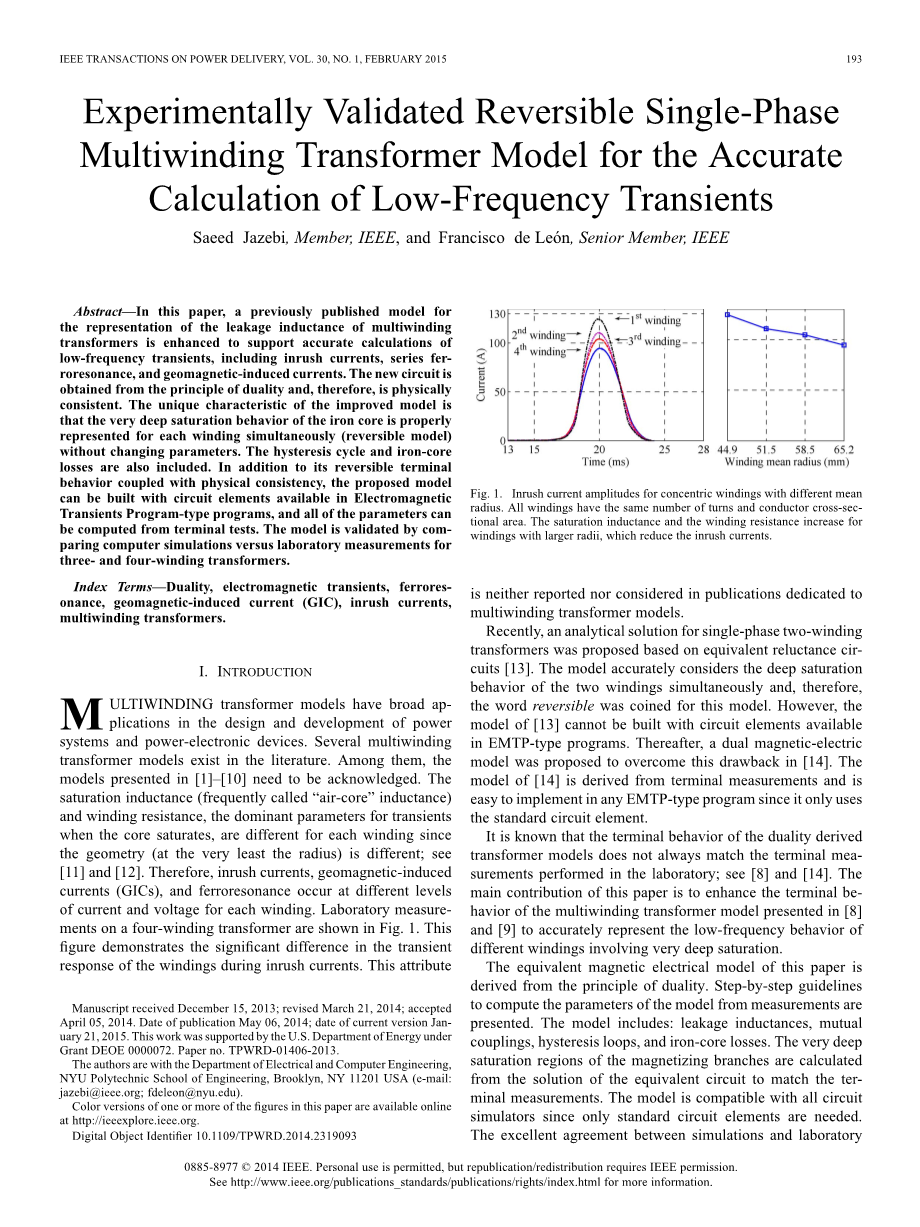
多绕组变压器型号在电力系统和电力电子设备的设计和开发中具有广泛的应用。 文献中存在几种多绕组变压器模型。 其中,需要承认[1] - [10]中提出的模型。 由于几何形状(至少在半径上)不同,饱和电感(通常称为“空芯”电感)和绕组电阻是铁芯饱和时的瞬变的主要参数,因此每个绕组都不同; 看到[11]和[12]。 因此,每个绕组在不同的电流和电压水平下都会发生涌入电流,地磁感应电流(GIC)和铁磁谐振。 四绕组变压器的实验室测量结果如图1所示。这显示了在涌入电流期间绕组瞬态响应的显着差异。 这个属性
手稿于2013年12月15日收到; 2014年3月21日修订; 2014年4月5日接受。出版日期2014年5月6日; 日期目前版本2015年1月21日。这项工作得到了美国能源部的资助DEOE 0000072的支持。 TPWRD-01406-2013。
作者是美国纽约布鲁克林纽约大学工程学院电气与计算机工程系11201(电子邮件:jazebi@ieee.org; fdeleon@nyu.edu)。
本白皮书中的一个或多个图形的颜色版本可在网上查阅http://ieeexplore.ieee.org。
数字对象标识符10.1109 / TPWRD.2014.2319093
图1.不同平均半径同心绕组的励磁电流幅值。 所有绕组的匝数和导体横截面积相同。 半径较大的绕组的饱和电感和绕组电阻增加,从而降低浪涌电流。
在专用于多绕组变压器模型的出版物中既未报告也未考虑。
最近,基于等效磁阻电路[13]提出了单相双绕组变压器的分析解决方案。 该模型准确地考虑了两个绕组的深饱和行为,因此,该模型创造了可逆字。 然而,[13]的模型不能用EMTP型程序中的电路元件构建。 此后,提出了一个双磁电模型来克服这个缺点[14]。 [14]的模型来源于终端测量,并且易于在任何EMTP类型的程序中实现,因为它只使用标准电路元件。
众所周知,对偶导出的变压器模型的终端行为并不总是与实验室中进行的终端测量相匹配; 见[8]和[14]。 本文的主要贡献是提高[8]和[9]中介绍的多绕组变压器模型的终端行为,以准确表示包含非常深饱和的不同绕组的低频行为。
本文的等效磁电模型是从二元性原理推导出来的。 介绍了根据测量计算模型参数的逐步指导。 该模型包括:漏感,互耦,磁滞回线和铁芯损耗。 磁化分支的非常深的饱和区域由等效电路的解决方案计算以匹配终端测量值。 该模型与所有电路仿真器兼容,因为只需要标准电路元件。 模拟和实验室之间的良好一致性
0885-8977copy;2014 IEEE。 允许个人使用,但重新发布/再发行需要IEEE许可。
看到http://www.ieee.org/publications_standards/publications/rights/index.html 了解更多信息。
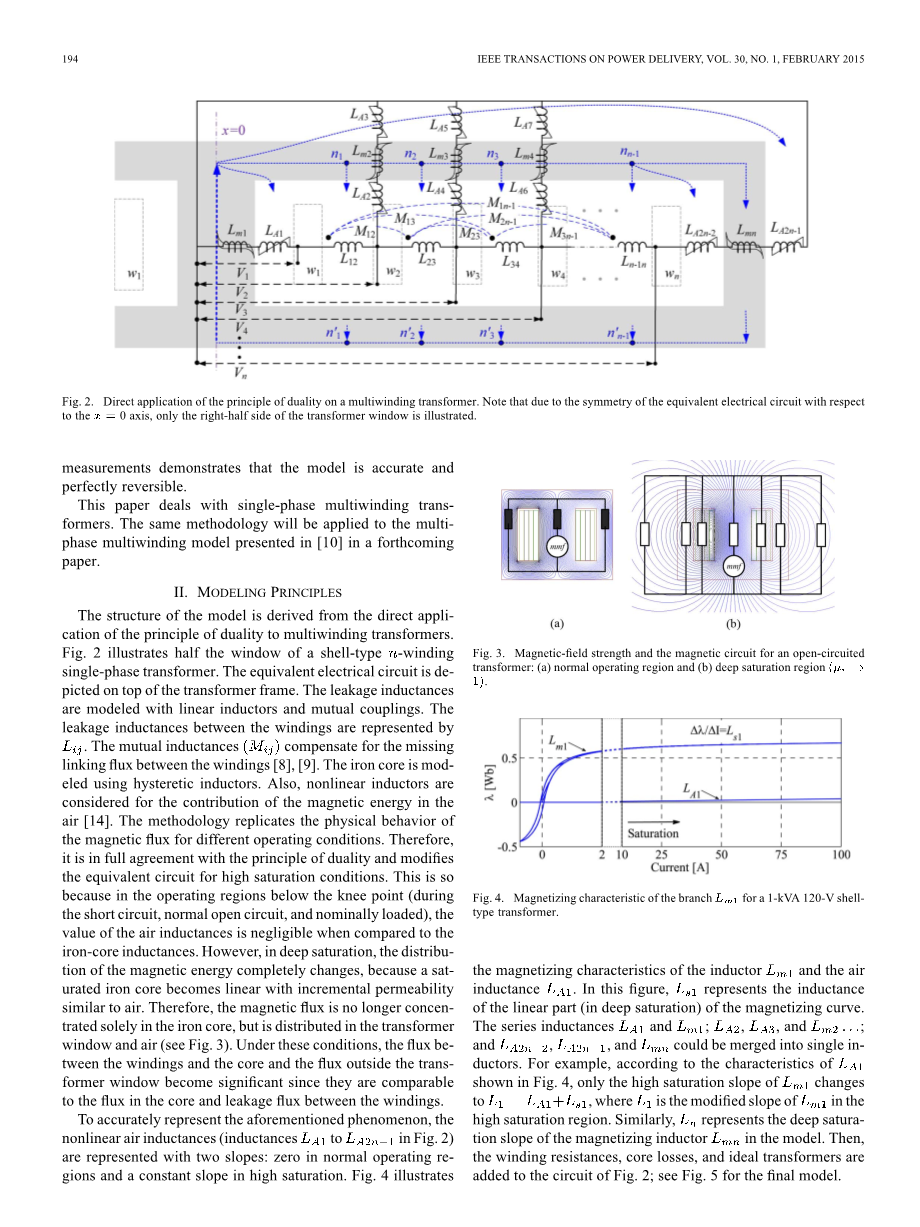
图2.在多绕组变压器上直接使用双重原理。 请注意,由于等效电路相对于电路的对称性 0轴,只显示变压器窗口的右半边。
测量结果表明该模型是准确的并且完全可逆。
本文涉及单相多绕组变压器。 在即将发表的文章中,将采用同样的方法应用于[10]中介绍的多相多绕组模型。
- 建模原则
该模型的结构来源于直接将对偶原理应用于多绕组变压器。 图2显示了壳式绕组单相变压器窗口的一半。 等效电路描述在变压器框架的顶部。 漏电感用线性电感和互耦进行建模。 \表示绕组之间的漏电感。 互感\补偿了绕组[8],[9]之间的连接缺失。 铁芯采用迟滞电感进行建模。 此外,非线性电感被认为是空气中磁能的贡献[14]。 该方法复制了不同操作条件下的磁通量的物理行为。 因此,它完全符合二元性原理并且模拟了高饱和条件下的等效电路。 这是因为在膝点以下的操作区域(短路期间,常开路和名义负载),与铁芯电感相比,空气电感的值可以忽略不计。 然而,在深度饱和的情况下,磁能的分布完全改变,因为饱和铁芯变得与空气类似的增量磁导率呈线性。 因此,磁通量不再集中在铁芯中,而是分布在变压器窗口和空气中(见图3)。 在这些条件下,绕组和变压器外部的绕组之间的通量和变压器窗口之间的通量变得很重要,因为它们与绕组之间的绕组和绕组之间的泄漏相当。
为了准确地表示上述现象,非线性空气电感(电感la1/电感la2在图2中)用两个斜率表示:正常工作区域为零,高饱和度为恒定斜率。 图4说明
图3.开路变压器的磁场强度和磁路:(a)正常工作区和(b)深度饱和区\
.
图4.分支的磁化特性/用于1-kVA 120-V壳式变压器。
电感器的磁化特性LM1和空气电感LA1。 在此图中,LS1表示磁化曲线的线性部分(深度饱和)的电感。 串联电感和LA1和LM1 .LA2,LA3和LM2;LA2n-2,LA2n-1,Lmn可以合并成单个电感器。 例如,根据图4所示的特征,只有La1的高度饱和斜率变化为Lm1,其中L1是高饱和度区域中Lm1的修正斜率。 类似地,Ln表示模型中磁化电感器Lmn的深饱和斜率。 然后,将绕组电阻,铁心损耗和理想变压器加到图2的电路中; 最终模型见图5。
图5.包括电阻和理想变压器的可逆多绕组变压器模型; 是用于改变高饱和区模型的终端响应的绕组饱和电感。
这个模型与[8]的模型不同的主要优点是计算了磁化电感器Lmn的深饱和电感。 请注意,根据图1和2的等效电路。 如图2和5所示,滞后磁化电感器与每个绕组的端子并联连接。 这些本文通常将电感称为磁化或非线性分支。分支的存在提供足够的自由度以正确表征不同的等效电感值
终端在饱和区。
如前所述,在正常工作条件下,铁芯和空气的电磁行为不同于深度饱和。 因此,磁化分支的建模分两步进行:首先,在拐点以下的非饱和区铁芯的非线性行为被认为包括滞后现象; 其次,加入深度饱和铁芯的线性行为。 以下小节介绍了计算模型未知参数的指导原则。
- 磁化分支:磁滞曲线
在一个额定电压激励的开路变压器中,铁心在拐点以下工作,其中磁化电感的值远大于漏电感。 因此,泄漏电感及其相互耦合与磁化电感相比可忽略不计。 请注意,在标称电压励磁的标准化开路测试中,磁通集中在铁芯中。 因此,通过对不同绕组的测量获得类似的磁滞曲线和磁化参数/和/)。 这已经通过在测量精度内在额定电压下激励时在所有绕组中测量几乎相同的磁化电流来进行实验演示。
在正常工作区域中,考虑到腿/轭的几何比例,测量的/ /特性可以分布在磁化分支之间。 由于不存在泄漏电感,所以图2的非线性分支有效地并联。 请注意,可以使用[15]的方法估算设计细节,如铁芯和绕组的尺寸。 尽管如此,为简单起见,假定变压器窗口是方形的。 因此,腿的长度与轭的长度相同。 另外,假设两者之间的距离
相邻的绕组是相同的。 因此,泄漏点在位于\o的点处离开轭
轭的长度(见节点在图2中)。 因此,肢体被物理分成导致的区域。 除了因为通常中心腿的宽度是侧腿的宽度的两倍,并且ux路径的长度是相同的(节点之间的距离 ,和
在图2中)。 最后,对于绕组变压器,[9]的方法扩展如下:
(1)
其中/是从任何绕组测量的磁化电感。 因此,用以下表达式获得每个分支的特性:
(2)
其中//是第n个非线性分支的磁化曲线,并且是数据的第th点。 积分的梯形法则应用于从开路测试获得的测量终端电压计算。 请注意,电流I是在初级(低电压)绕组中测量的,而感应电压在开路的次级(高电压)绕组上被捕获。
- 磁化分支:深饱和区域
开路变压器的磁路由连接到\的几个并联支路组成(见图3)。 电路可以简化(通过串/并联组合),产生单一的非线性磁阻,具有正常条件下的滞后特性和深度饱和下的线性特性。 这个模型的双电表示是一个单一的滞后分支。 因此,变压器模型在开路条件下的最简单的双重表示是与相应绕组的终端电阻串联的单个迟滞电感器。 这可以在图6(a)和(b)中看到双绕组变压器的第一和第二绕组。
图6.双绕组变压器的对偶派生模型的基础结构 (a)所有开路条件下的第一绕组的最简单的双重表示; (b)所有开路条件下第二绕组的最简单的双重表示; (c)增加漏感以考虑短路和正常负载条件下泄漏ux的贡献。 /,/和/的联合关系影响变压器的开路特性,特别是在深度饱和的情况下。
请注意,漏电感在开路条件下没有物理存在(因为只有一个绕组通电时没有泄漏)。 但是,为了模拟正常工作条件,一个模型需要表示两个绕组之间的泄漏(至少有两个绕组通电时)。 为了在开路和短路情况下具有独特的模型,需要根据图6(c)将泄漏组件添加到电路中。 然而,漏电感的增加会影响图6模型的开路状态,特别是在深饱和区域。
当变压器在开路条件下工作在拐点以下时,漏感可忽略不计。 这是因为磁化电感远大于漏电感。 然而,对于更高的激励,磁化曲线的斜率衰减到深饱和电感的值 ,和/,它们的数量级与泄漏电感相同。 在这些条件下,考虑到漏电感是正常工作所必需的并且是模型的一部分(参见图2和5)的事实,等效电路中漏电感的影响不能被忽略。 这会导致终端测量结果与模型的行为不匹配
- 在深度饱和区域。 为了克服这个缺点,提出了通用公式来精确计算
和。
-
- 系统方程的推导:为了反映模型在深饱和状态下的终端行为,需要正确计算\。 图7示出了从三绕组变压器的不同端子看到的等效电路。 请注意,在每种情况下,由于仅测量饱和电感,所以次级绕组和三次绕组都开路并且将阻尼元件移除以进行分析。 如[12]中推荐的,初级绕组由一个混合\电压源激励,以驱动变压器进入深度饱和状态。 建模技术基于终端测量; 因此,该模型的拓扑结构对于有或没有油箱,磁性油箱分流器,皮带等的变压器而言是一致的。然而,在存在这些变压器部件时会影响深饱和电感测量,这会改变\的值。 术语“空心电感”[12]只能用于空心线圈或没有铁心和油箱的变压器。 因此,在本文中,它是
图7.用于计算三绕组变压器饱和电感的等效电路; 从(a)第一个绕组看到的简化电路,
(b)第二绕组,以及(c)第三绕组。
用[饱和电感]代替[16]。 作为ac/dc激励的结果,所有三个磁化分支都工作在线性饱和区。 因此,这些分支用深饱和区域的对应恒定斜率部分表示L1,L2和L3)。 图8示出了从深度饱和的四绕组变压器的端子看到的等效电路。 如图9所示,为绕组变压器导出类似的电路。
第一步是获得从模型端子看到的等效电感关于变量。 如图1和2所示,明智地选择网格,包括方向和编号7-9,对于获得适用于泛化的简化方程是必不可少的。 这些网格方程式是针对电压和电流的基本分量编写的,其中是混合电压源的基本分量,如下所示:
(3)
电流和电压矢量如下:
(4)
该 三,四和绕组变压器的矩阵如下所示:
(5)
图8.用于计算四绕组变压器四个端子饱和电感的等效电路; (a)第一绕组,(b)第二绕组,(c)第三绕组和(d)第四绕组看到的简化电路。
\ 对于三绕组变压器,除以下部件外都是零:
(6)
对于四绕组变压器,以下元件非零:
.
(7)
绕组变换器矩阵的非零元素如下:
(8)
该 矩阵写法如下:
. . . (9)
三绕组变压器的/哪里
(10)
对于四绕组变压器,I是
(11)
对于卷绕变压器,(12)给出了/矩阵,如页面底部所示。
-
- 系统方程的解答:空芯电感 从每个绕组看到的电流由以下表达式计算得出(见图7-9):
(13)
等式(13)可以代入(3)。 请注意,(3
全文共11417字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[11203],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。