
英语原文共 8 页,剩余内容已隐藏,支付完成后下载完整资料
高压变电站中开关引起的瞬态电磁场计算
摘 要:断路器和隔离开关的开关操作会在辐射高压变电站内辐射瞬变电磁场。产生的磁场可能会干扰并破坏电子设备的正常运行。因此,该电子设备的电磁兼容性(EMC)必须早在变电站规划和运营的设计阶段就被考虑。此外,分布式微电子器件被引入变电站环境中,并且更加靠近开关站中的开关设备。因此,有必要重新对变电站环境进行EMC评估,以解决这些问题。本文使用时域有限差分(FDTD)方法计算由于典型的高压空气绝缘变电站(AIS)进行切换而引起的瞬变电磁场。
关键词:气体绝缘变电站;电磁兼容性(EMC);电磁场;时域有限差分(FDTD);开关瞬态
1 引言
变电站的电磁环境可以通过测量或计算来表征。由于开关引起的电磁场发射的测量涉及复杂且昂贵的设备。替代方法是开发模型以预测发射量。替代变电站模型可以用来帮助理解测量结果,并提供估算超出测量限制的电磁干扰水平的方法[1]。一旦模型被证明是可靠且准确的,它们就有可能大大简化分析过程。
自从在电力系统中引入自动化和控制以来,已经开发了各种变电站模型,特别是在变电站中[2]–[5]。即使存在这些模型,[1],[6]中建议进行进一步研究,以确定变电站环境中可能发现的不同材料和结构对瞬变场的影响,例如变压器,支撑结构,接地网和土壤成分。最初,瞬态场预测的重点主要在于辐射场如何影响控制室,因为大多数电子设备都位于此处。
有建议认为,在控制室中,来自母线的辐射干扰的影响可能不明显[7]。这是因为假定母线辐射不明显。并且从母线到控制室的距离对于任何辐射场而言都非常大,以至于在到达电子设备之前减小到可以忽略的值。但是,变电站中使用的设备已经发生了很大的变化,并且变得非常复杂。而且,最重要的是,已经引入变电站的一些新的电子设备不必再安装在控制室中。它可能位于开关设备附近或开关场中的干扰源附近。这在开关站中被称为“分布式电子设备”[8]。为了在变电站中成功引入和运行这种新设备,必须保证它在恶劣的环境中不受干扰。因此,需要考虑开关设备附近的地点来评估开关站中的瞬变电磁辐射。FDTD方法可用于模拟上述情况并有效预测电磁场。
为了计算变电站中的瞬变场,需要沿母线传播的瞬变电流。不需要使用实际的母线电流,衰减的正弦电流和频率变化的正弦电流已很好地代表了变电站中的瞬态电流,并且已被用于计算本研究中的辐射场。在能够应用假定电流来进行场计算后,下一步就是找到合适的方法来计算母线上的实际瞬态电流,包括模型中开关元件的物理特性。这样获得的电流可以用于计算瞬变场。首先将使用FDTD代码获得的简单电磁场瞬变模型的结果与相似环境中的分析方法进行比较,然后,将给出典型高压变电站中简化母线部分的仿真结果。
2 场计算的分析和FDTD方法
变电站中瞬态电磁场的计算实际上是一个两步过程[2]:
步骤1:计算由于开关引起的导体上的瞬态电流;
步骤2:计算由于电流而在导体附近产生的辐射场。
电磁场可以通过分析或数值方法来计算。赫兹偶极子方法[4],[9]或分析方法[10]-[12]假定线路或导体(在这种情况下为变电站母线)为圆柱形。假定母线半径与瞬态电流的最小波长相比较小,因此该电流可以看作是细丝电流。
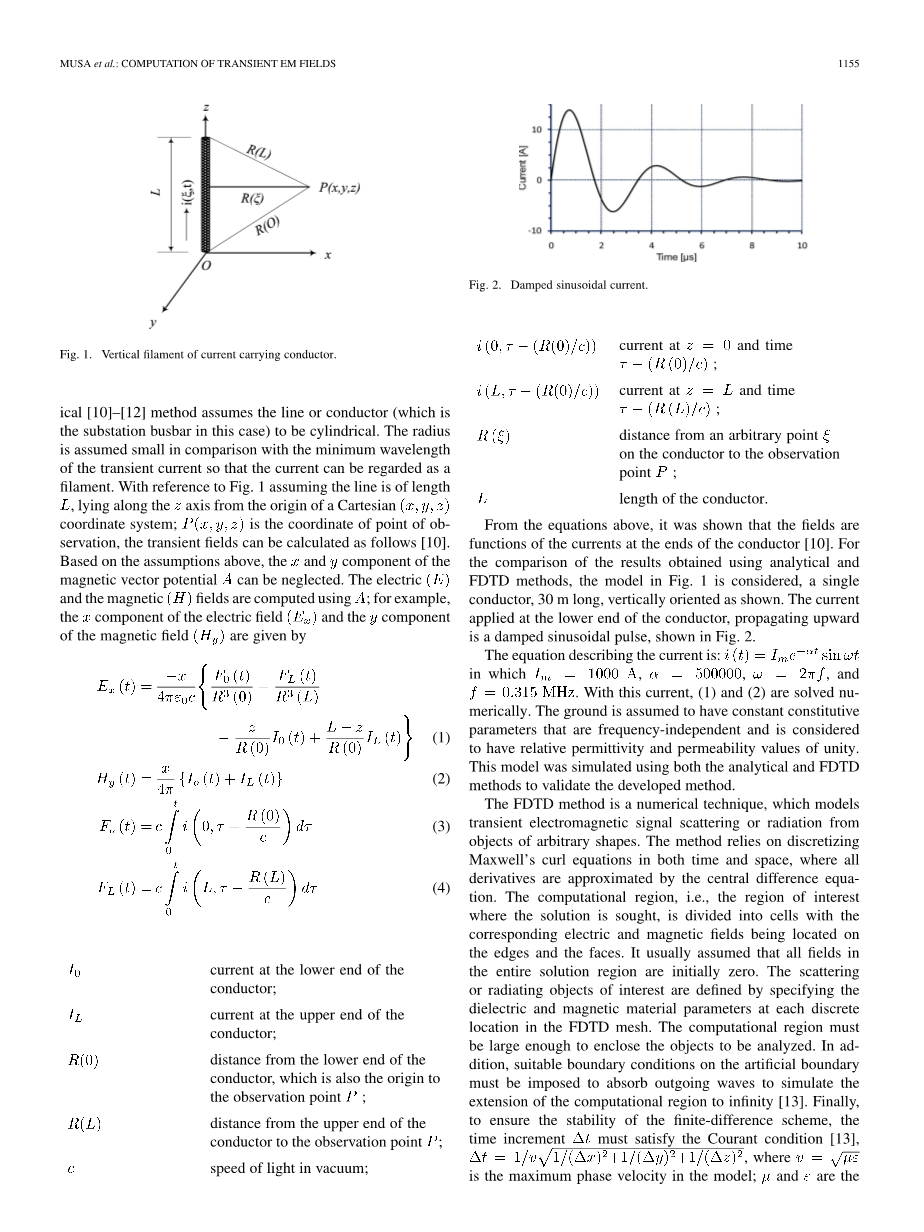
图1 载流导体的垂直细丝电流
参照图1,假设直线的长度为L,并沿z轴将一端放在直角坐标系的原点。如果是观测点的坐标,则瞬态场可以如下计算[10]。基于以上假设,可以忽略和方向磁矢量势分量。电场(E)和磁场(H)就可以使用磁适量势来计算。例如,设电场的方向分量为那么磁场方向分量为由下式给出:
从上面的等式可以看出,场是导体[10]端部电流的函数。为了比较使用分析方法和V方法获得的结果,我们考虑了图1中的模型,该导体是长30m的单根导体,如图所示垂直放置。施加在导体下端的电流向上传播是一个衰减正弦脉冲,如图2所示。
图2 衰减正弦电流
电流方程为:其中,,,。基于以上电流,可以对(1)和(2)进行数值求解。假定地面具有恒定的基本参数,这些参数与频率无关,并且被认为具有单位相对介电常数和磁导率。使用分析方法和FDTD方法对该模型进行了仿真,以验证所开发的方法。
FDTD方法是一种数值技术,可对来自任意形状物体的瞬态电磁信号散射或辐射进行建模。该方法依赖于在时间和空间上离散麦克斯韦的旋度方程,其中所有导数都由中心差分方程近似。计算区域,即寻求解的区域,被划分为单元,其相应的电场和磁场位于边缘和面上。通常假定整个解区域中的所有初值为零。通过指定FDTD网格中每个离散位置的介电和磁性材料参数,可以定义指定的散射或辐射对象。计算区域必须足够大以包围要分析的对象。另外,必须在人工边界上施加合适的边界条件以吸收输出波,以模拟计算区域向无穷大的扩展[13]。最后,为了确保有限差分方案的稳定性,时间增量必须满足Courant稳定条件[13],,其中是模型中速度的最大值;和介质的相对磁导率和介电常数。,,分别是,,方向上的空间网格增量。为了模拟以上情况,将空间增量设定为并且离散时间步长设定为Courant条件的95%即。应用完美边界层(PML)吸收边界条件[14]在人工边界上实现输出波吸收。
2.1 细线表示
基本FDTD代码的条件是,元大小必须与计算空间中的最小结构相当。变电站中的辐射元件主要是电缆和母线,它们的半径通常比元尺寸小。因此,必须将母线半径纳入问题的物理范围。为此,需要一种在FDTD中近似细线的方法。Noda[15]通过根据其半径校正邻近的电场和磁场来提出细线表示,并将其用于电涌仿真。本文采用这种细线表示法,导体半径设置为0.025m。虽然发现使用细线表示法(其时间增量为Courant稳定性条件的99%)会引起数值不稳定[16],但在95%的条件下并未出现不稳定情况。
2.2 母线与地的反射
在瞬态场计算的分析方法中,未考虑导线末端的反射,因为假定电流突然在一端“出现”并最终在另一端“消失”而没有反射。在此处采用的FDTD公式中可能不满足这些标准。当然,在截头导体的末端应该有反射;尽管如此,FDTD方法通过将导体的上端置于计算空间的边界来解决了这种情况。
对于由于地面引起的反射,必须使用坡度法或赫兹方法,使用单独的技术来解决反射问题。例如,[2],[6]使用基于菲涅尔反射系数和递归卷积的方法,而[4],[5]则使用图像方法。但是,在FDTD公式中,必须指定位于接地区域内的点处的电导率,介电常数和磁导率。然后,由于地面引起的反射会自动纳入计算中,这是FDTD方法的优点之一。
计算中使用的大地参数如下[2],[17]:,,。
指定所有参数后,在FDTD空间中建立了图1中的模型并进行了仿真。如图所示,电流施加在导线的下端,并向上传播。瞬态场计算假定两端都匹配。图3和图4表明在距离导体中心10m,20m和50m的点,电磁场分量和在运用分析方法和FDTD方法计算时是相同的。表格1展示了两种方法在相同点计算出的峰-峰值大小,可以发现两种方法在幅值和相位上具有较好的一致性。
图3 距导体中心10m,20m,50m处由衰减正弦冲击产生的电场z分量
图4 距导体中心10m,20m,50m处由衰减正弦冲击产生的磁场y分量
3 对高压空气变电站的部分建模
如果已知长度,半径和地上位置,则可以通过在FDTD网格中指定其基本参数来对变电站中的高压母线进行建模。然后可以确定代表开关电流的电源位置。为了使用FDTD方法对高压变电站的更具代表性的部分进行瞬态现场仿真,需要对计算网格进行规范,包括接缝和折弯。随着变电站复杂性的增加,编程和计算资源也随之增加。这甚至可能需要采用网格生成算法。这里描述的简单变电站模型是达到这一目标的一个步骤。典型的总线长度为20-80m长,位于地面以上5-15 m。因此在FDTD空间中设置了50m长,位于地面11m以上由三个平行母线组成的母线段。(如图5所示)。母线的末端距离10网格完美匹配的层边界2.5m。该模拟考虑了两种不同的地面条件:不良传导的地面和良好传导的地面。两种情况下使用的导体半径均为0.05m。选择不理想的地面特性如下:相对介电常数为10,电导率为0.01S/m,相对磁导率为1。在这两种情况下,均使用频率变化的正弦电流。频率从1MHz到50MHz以不连续的步长变化。选择的频率范围包含高压变电站瞬态中预期的频率。通常,开关浪涌可能会产生比这更少的频谱。但是,可能会在此范围内发生短时电涌[1]。这也将使得能够分析由变化频率电流产生的场。
图5 应用在高压变电站模型中的三相母线部分(a)侧面图(b)端视图
如图5所示,电流从导体中部距一端10m处施加,并沿轴正方向传播,从而模拟了充当天线的总线部分。电流的峰值幅度选择为1000A,以模拟由于开关引起的高压总线电流瞬变。空间增量设定为并且在95%的Courant条件下设定时间步长为。计算域的体积设定为,,。,与分别为x,y,z方向上的尺寸。和上文一样使用完全匹配的层吸收边界条件。
计算分析直接位于开关下方的三点A,B,C的电磁场。参照图5,A点位于总线下方2m,B点位于总线下方5m,C点位于总线下方10m(离地1m)。点的坐标如图5(a)所示。图5(b)显示了导体和x-y平面中的三个点。
图6 在不良接地条件下,施加正弦电流,在三处位置上电场随频率的变化。(a)A处场(b)B处场(c)C处场
3.1 电源频率变化作用
图6显示了不良好地面条件下三个点的电场分量,,。
除了在低频时分量更大,其余情况是主分量。在A点处,主场随频率增加几乎保持恒值。在B点上,该场随着频率的增加而略有增加,直到大约30MHz,然后又开始减小。
出现这种情况这可能一方面因为存在大地,另一方面由于存在电源,因为该点位于两者之间的一半。 在这里,电场的分量几乎可以忽略不计,并且变化完全由预期决定的主导,这是由于辐射体的方向是朝向z向的。随着频率增加到大约35MHz,不断增加。在C点,随着频率增加到大约35MHz,和不断增加。
图7 在良好接地条件下,施加正弦电流,在三处位置上电场随频率的变化。(a)A处场(b)B处场(c)C处场
图7显示了在相同A,B,C位置处于良好地面条件下的电场分量。
在A点(远离地面),各方向的E分量几乎没有区别。在B点,主要变化的是。在C点(接近地面),和有所不同。没有明显变化。
图8显示了在相同A,B,C位置处于变电站良好地面条件下的磁场分量。在所有情况下,与其余场相比,可以忽略不计,这也是z向定向电流所造成的。比约大5倍。对于距离地面较远的点A,B,尽管该关系不是线性的,但磁场通常会随着频率的增加而减小。而且,这些场在大约5MHz时具有很高的幅度。对于靠近地面的点C,场的行为与上述点有很大不同。在这一点上,磁场强度随着频率的增加而增加,直到大约35MHz。这可能是由于靠近地面,感应电流将在其中贡献磁场。此外,这些场在大约5MHz时具有很高的幅度。这可能是由于母线的长度与频率相关的共振效应所致。在此频率下,由于母线的长度为50 m,波会产生共振,因此场值较高。
图8 在良好接地条件下,施加正弦电流,在三处位置上磁场随频率的变化。(a)A处场(b)B处场(c)C处场
图9显示了不良好地面条件下变电站内相同A,B,C位置磁场的,,分量。
对于点A,B,C,场的变化与良好导电地面有相同的趋势。对于点C,相比良好地面,磁场随频率的变化更小。随着频率从5MHz增加到大约35MHz,磁场变化几乎是平坦的。比较图8(c)和9(c),由于在不良好的地面中感应电流的损耗增加,所以场在开始时水平相当,但是在高频处衰减。
3.2 场随距离的变化
图10和11分别总结了不良好地面条件下电场和磁场强度随距离的变化。场强由下式确定:
图9 在不良接地条件下,施加正弦电流,在三处位置上磁场随频率的变化。(a)A处场(b)B处场(c)C处场
通常,随着从母线到地面的距离增加,电场强度和磁场强度的大小都会减小。但是,在35MHz时,电场的强度C点高于B点。另外,在50MHz时,磁场强度C点高于B。这些可以通过仔细观察图10(c)和11(c)得到。
图12和13分别显示了良好地面条件下电场和磁场强度随距离的变化。与处于不良好的地面情况下一样,电场与磁场都随着从母线到地面的距离增加而减小。但是,C点的磁场强度在35MHz和50MHz处要比B点高。同样,在45MHz时,B点的磁场也要比A点的磁场高。参照图13(
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[238548],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


