英语原文共 4 页,剩余内容已隐藏,支付完成后下载完整资料
三相三电平中点钳位准Z源DC/AC电感耦合可行性研究
摘 要:本文介绍了一种可行性较强的三电平耦合电感实现的研究中性点钳位准Z源DC/AC转换器。我们的理论验证表明,耦合qZS电感器可以减小尺寸和重量磁性元件或输入电流纹波。数学分析的结果显示了电感的差异可改变电路参数下的电流。旨在模拟提供的结果以验证我们的理论假设。
关键字:DC/AC转换器,三电平逆变器,耦合电感器,准Z源
内容介绍
最近的研究表明,三级中性点钳位准Z源逆变器(3L NPC qZSI)基于DC / AC转换器的性能是有效的可靠[1] - [4]。图1是一般电路图基于3L NPC qZSI的单相DC / AC转换器的电路拓扑图。转换器的主要优点是与类似的拓扑相比,可连续输入电流,输入电压稳定值和击穿电压较为良好。但是,由于大量的被动组件两个qZS网络(L 1,L 2,C1,C2,D1和L3,L4,C3,C4,D2),整体3L-NPC-qZSI的尺寸和重量比较大。这导致需要优化或减少无源元件。
在某些情况下,耦合电感的实现(两个一个磁芯上的电感器是一种有效的解决方案减少由于焊剂引起的绕组匝数倍增效应。此外,如果匝数仍然是同样,然后是电感电流纹波以及输入电流纹波可以降低[5] - [9]。
本文介绍了一项分析和模拟研究qZS网络磁场的集成可能性元素,以减少整体的尺寸转换器。同时,主要电参数转换器应保持与单个转换器相同磁性元件。
图1 单相三电平中点钳位准Z源逆变器(3L-NPC-qZSI)的电路拓扑图。
电感耦合的数学分析
为了减少所提出来的建议物理参数3L-NPC-qZSI(图1),几种电感组合可以考虑耦合。图2给出了DC直流链路电流的典型波形。 我们可以看出,它包含直接和替代组件。通过傅立叶分析可以很容易地估算替代组件的基波谐波:
同时,这股电流流过qZS网络并唤起电感器中的低频振荡。这种电流纹波严格依赖于被动元件特别是电子耦合和电感耦合。
图2 DC直流链路电流波形
图3和5示出了一般的等效电路电路图与不同的电感耦合可能性。在两个图中(图3和5),逆变器是用对应的正弦电流源代替消耗的电流的一次谐波分量逆变器。 逆变器是系统中唯一的低频电流纹波源.对于电路分析,使用对称qZS网络的线性化模型。由于逆变器是低频的唯一来源电流纹波,我们可以应用减少的叠加定理和复阻抗分析电路的AC行为。在两种耦合情况下研究的主要参数分别是电感器L1和L2的交流电流(电流纹波)L1和L2的基本分量。
2.1电感器L1与L3的耦合和L2与L4的耦合
图3描绘出所提出的转换器的简化等效电路,其中L3电感器与L1电感器耦合,L4电感器和L2电感器耦合。逆变器用电流源dc代替,并且等效的有效电阻为R,R其还包括电感器绕组的有效电阻。
图3当L1与L3耦合时,3L-NPC-qZSI的等效电路L2与L4耦合
这种耦合对电流没有任何影响,因此耦合电感器中的电流相等。 在这种情况下,基本方程可以表示为
Idc=IL2 IC1
Idc=IL1 IC2
IL2bull;xL2 IL2bull;R =IC1bull;xc1 (2)
IL1bull;xL1 IL1bull;R =IC2bull;xC2
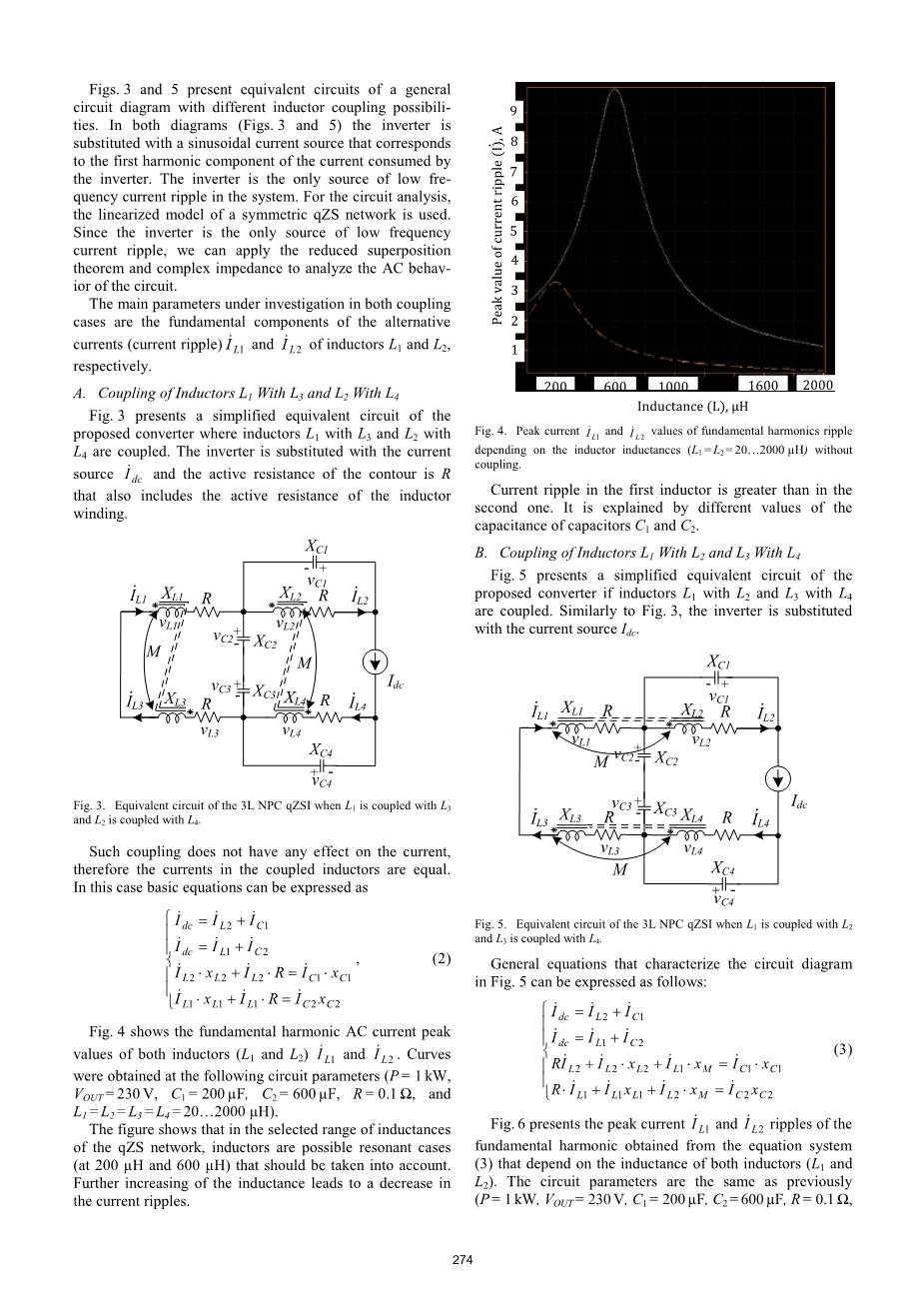
图4显示了基波谐波AC电流峰值两个电感的值(L1和L2) L1和L2。
可通过以下电路参数计算获得 P=1KW, Vout=230V,
C1=200mu;F, R=0.1Omega;, C1=600mu;F, L1= L2 =L3 =L4=400mu;H
该图显示了在所选择的电感范围内在qZS网络中,电感器可能出现谐振情况(应在200mu;H和600mu;H时),我们应考虑到这一点。在目前的电路纹波中进一步增加电感导致电感减小。
图4 无电磁耦合的电感L1和电感L2时基波谐波的峰值电流L1和L2值变化图
第一个电感L1中的电流纹波大于第二个电感L2。 它通过不同的电容器C1和C2的电容值来达到变化的目的。
2.2 电感器L1与L2的耦合和L3与 L4的耦合
图5给出了简化的等效电路。如果电感器L1与电感器L2耦合并且电感器L3与电感器L4耦合,则构成另一种转换器耦合。 与前面的图3相类似,逆变器可使用电流源dc进行替换。
图5 当L1与L2耦合时,3L-NPC-qZSI的等效电路L3与L4耦合
典型电路拓扑图(图5)的一般方程式可以表示如下:
Idc=IL2 IC1
Idc=IL1 IC2
IL2bull;xL2 IL2bull;R IL1bull;xM=IC1bull;xc1 (3)
IL1bull;xL1 IL1bull;R IL2bull;xM=IC2bull;xC2
图6显示了从等式系统(3)计算获得的基波谐波的峰值电流纹波L1和L2,它取决于两个电感器(L1和L2)的电感。电路参数与以前相同,具体情况如下所示:P=1KW,Vout=230V, C1=200mu;F, R=0.1Omega;, C1=600mu;F, L1= L2 =L3 =L4=400mu;H
除了在这种情况下,互感M也起到一定的作用,并且每个电感器产生的互感也应是相同的,即L1 = L2 = L3 = L4 = M。也就是说,互感M对应于电感器之间的完全耦合。总磁阻的构成与前一种情况相同,那么磁值也应是与前一种情况相同。
图6 存在电磁耦合的电感L1和电感L2时基波谐波的峰值电流L1和L2值变化图
从上述的两种情况我们可以看出,耦合设计与非耦合设计相比,谐振现象有着略微减轻。同时,第二电感L2中的电流纹波大于第一电感L1中的电流纹波。 耦合之后虽然电流纹波发生了变化,但是两个电感器的总电流纹波明显降低。
图7显示了恒定电路参数下基波谐波的峰值电流和纹波P=1KW, Vout=230V, C1=200mu;F, R=0.1Omega;, C1=600mu;F, L1=L2=400mu;H和可变互感M=0~400mu;H
图7 电感L1和L2为恒定值,互感值M对于基波谐波的峰值电流值L1和L2的影响图
图7显示了互感M对电感中的电流纹波所产生的影响。
第三章 仿真结果
为验证我们的数学分析,3L-NPC-qZSI开发了PSIM仿真软件模型,使得耦合电感的不同组合得到了验证。在所存在讨论的情况下,转换器操作模式均处在连续传导模式(CCM)中。
3.1 电感器L1与L3的耦合和L2与L4的耦合
图8表示电感器L1和L2的电流。正如预期的结果一样,输入电流会以两倍电网工频频率进行波动(100赫兹)。
图8 电感L1和L2中基波谐波的峰值电流L1和L2实时变化图
仿真模型的电路参数如下:电感器的电感(L1,L2,L3,L4)取5 mH,互感为0 H,电容器电容取值为C1 = C3 =600mu;F,C2 = C4 =200mu;F,输入电压取200 V,输出电压取230 V的均方根值。所讨论的转换器工作在升压模式,直通占空比lt;
全文共4958字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[1552]
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。