英语原文共 10 页,剩余内容已隐藏,支付完成后下载完整资料
一种用于同步磁阻电机的具有减小转矩脉动算法的新型晶粒取向叠片转子铁心组件
Seyedmorteza Taghavi,IEEE学生会员,Pragasen Pillay, IEEE院士
摘要:高转矩密度和低转矩脉动对牵引应用至关重要,可以确保电气化动力系统在启动、加速和巡航过程中正确运行。冷轧晶粒取向电工钢等高质量各向异性磁性材料可用于配备有横向叠压式转子的同步磁阻电机以获得更高的的效率、转矩密度和紧凑性。然而,转子圆柱形的形状使得这些材料在磁极数高于两个时的使用更加困难。从减小转矩脉动的角度来看,特别注意转子槽距角的设计可以得到改进。本文提出了一种创新的转子叠片设计和组装方法,采用冷轧晶粒取向电工钢以实现更高的转矩密度,并具有用于减小转矩脉动的转子槽距角设计的算法。对设计方法和成型工艺进行了讨论,进行了有限元分析和实验,并将结果进行比较以验证所提出的方法。
关键词:汽车应用,晶粒取向钢,转子叠片,分段磁极,槽角,同步磁阻,转矩改进,转矩脉动,牵引电机
Ⅰ.引言
由于电动汽车在汽车工业中的推广,选择合适的电机对于电动动力系统至关重要[1]-[3]。因此对高性能、低成本电机的需求增长很快。同步磁阻电机(SynRM)中转子的各向异性几何形状便于减少使用昂贵的稀土永磁体以及转子结构中的铜棒或铝棒。结果,与永磁同步电机和感应电机相比,同步磁阻电机成本可能会更低[4]。如今,同步磁阻电机在电气化动力传动系统中具有很强的潜力[1],[5],[6]。
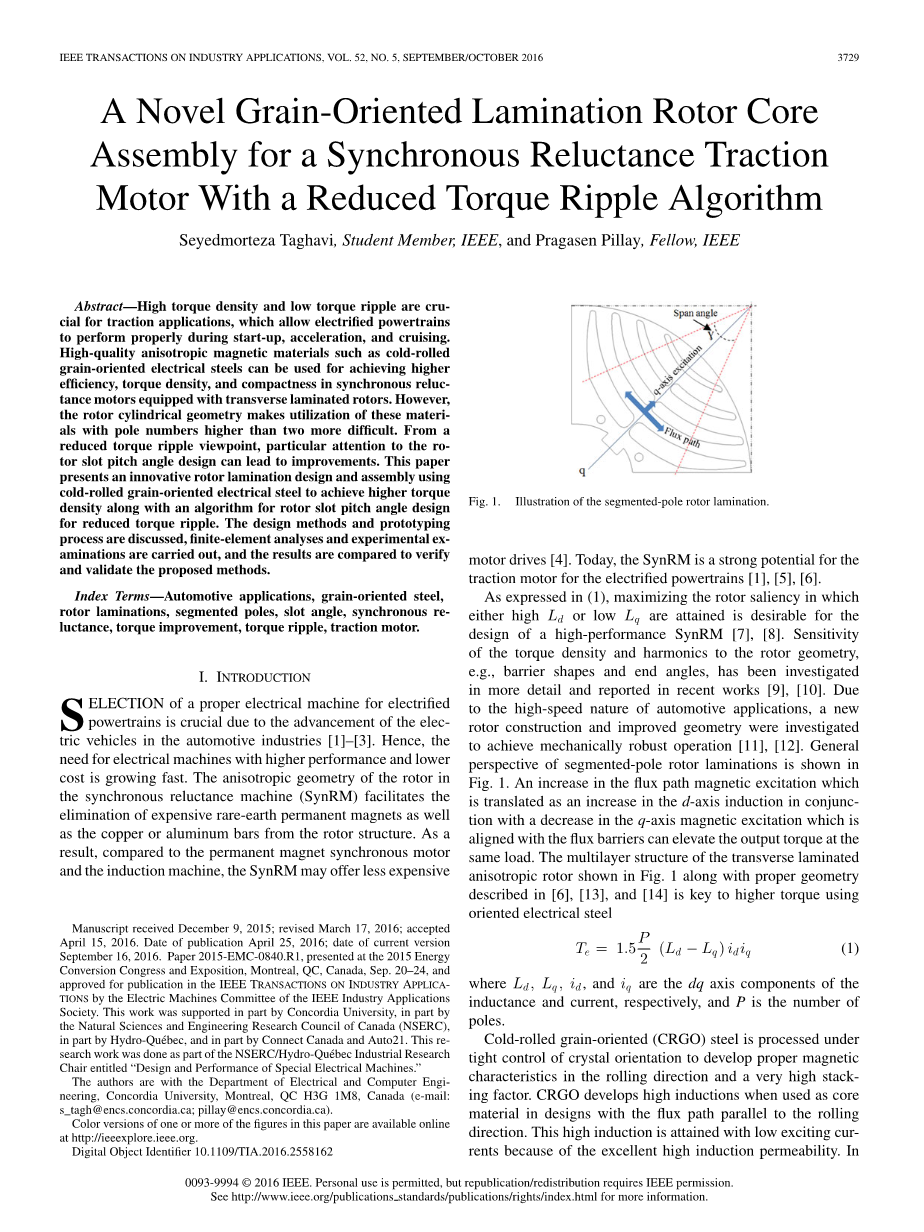
如在(1)中所表述的,在达到高Ld或低Lq的转子凸性最大化是设计高性能同步磁阻电机的理想选择[7],[8]。转矩密度和谐波对转子几何形状(例如磁障形状和端角)的敏感性已经被更详细地研究并在最近的工作中报告[9],[10]。针对汽车应用的高速特性,研究了一种新型转子结构和改进的几何结构,以实现机械稳健运行[11],[12]。分段磁极转子叠片的一般透视图如图1所示。磁路励磁的增加(其被转换为d轴磁感应的增加以及与磁障对齐的q轴磁感应的减少)可以提高相同负载下的输出转矩。图1所示的横向层叠各向异性转子的多层结构以及在[6]、[13]和[14]中描述的合适的几何形状是使用取向电工钢获得更高转矩的关键,
(1)
其中Ld、Lq、Id和Iq分别是电感和电流的dq轴分量,P是极数。
图1 分段磁极转子叠片图示
冷轧晶粒取向( CRGO )钢在晶体取向的严格控制下进行加工,以在轧制方向上形成适当的磁特性和非常高的占空系数。CRGO用作芯材当磁通路径设计为平行于轧制方向时会产生高感应。由于具有优异的高感应磁导率,这种高感应可以在低励磁电流下实现。此外,CRGO的正常工作电感远低于材料的磁饱和,以便在大多数设计中有一个充足的安全裕度。CRGO的高可用磁感应以及高占空系数可以实现紧凑的磁芯设计,这有助于减小尺寸和重量。CRGO的典型多向特性和磁通密度示于图2中。
图2 CRGO,AK钢的典型磁性特征
如该图所示,在轧制方向(0°)和与轧制方向成90°的角度上,磁性能是不同的。通过在与轧制方向相同的方向上应用材料获得最高的磁性能。与此相反,非取向电工钢在带材平面内表现出各向同性的磁性行为,这允许以任何取向应用这种材料。本文研究了平均转矩和转矩脉动。为了提高牵引电机的转矩密度,提出了一种采用CRGO的四极同步电机转子磁极组件。此外,还讨论了一种基于转子和定子槽距角的几何方法,以减小转矩脉动。相应地,本文提出了一种新的分析方法,用数学方法表示转子的适当槽距角,以获得较低的转矩脉动。制造了一个具有三个不同转子的7.5马力的样机,并对其进行了不同负荷下的试验。通过计算机辅助分析与实验结果的比较,对该方法进行了评价。
Ⅱ.新型转子磁极装配方法
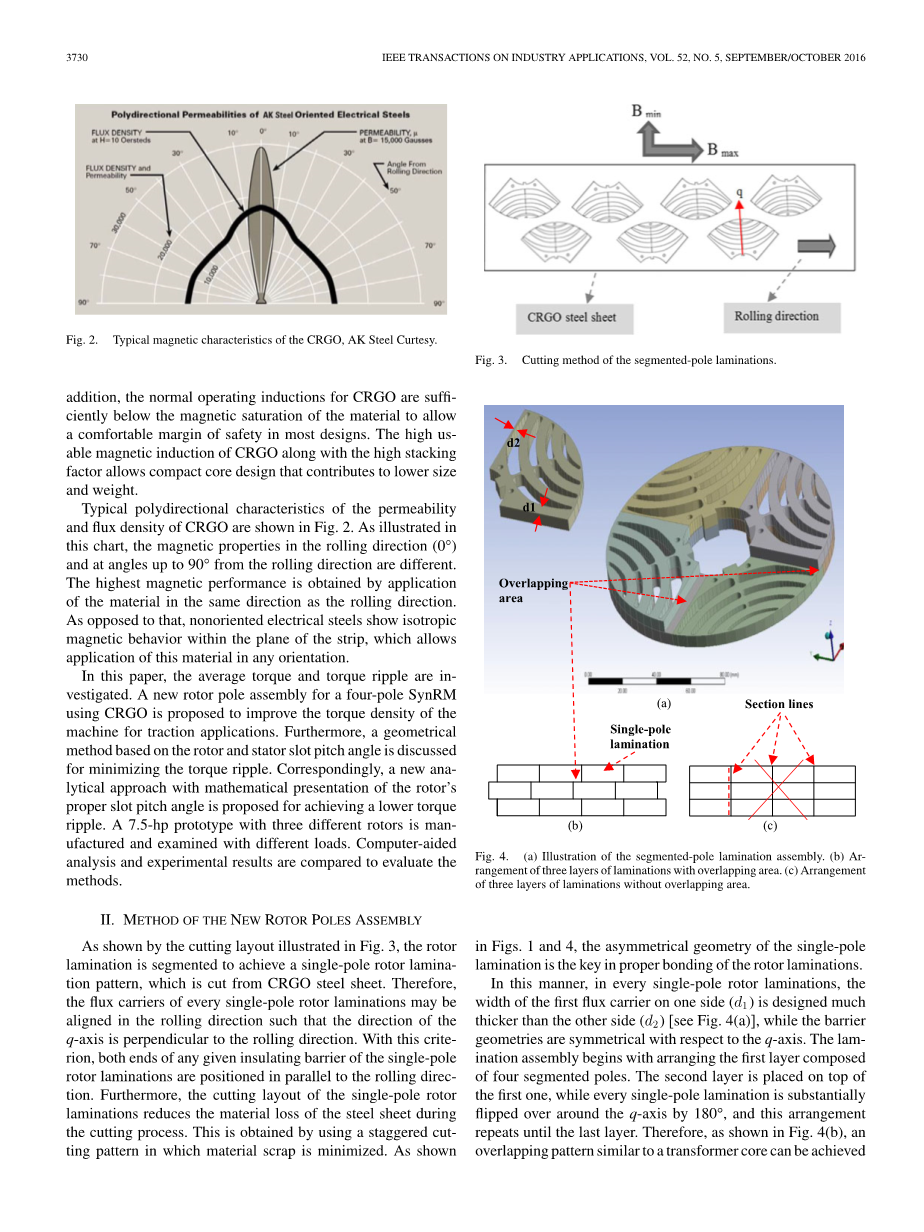
如图3所示的切割布局所示,转子分割层压以实现从CRGO钢板切割的单极转子层压图案。
图3分段叠片的切割方法
因此,每个单极转子叠片的导磁块可以在轧制方向上对齐,使得q轴的方向垂直于轧制方向。 根据这一标准,单极转子叠片的任何给定绝缘屏障的两端都与轧制方向平行。此外,单极转子叠片的切割布局减少了切割过程中钢板的材料损失。 这是通过使用材料废料最小化的交错切割模式获得的。如图1和图4所示,单极叠片的不对称几何形状是转子叠片正确连接的关键。
图4 (a)分段磁极叠片组件的图示 (b)有重叠区域的三层叠片结构
(c) 无重叠区域的三层叠片结构
以这种方式,在每个单极转子叠片中,一侧(d1)上的第一个导磁块的宽度设计得比另一侧(d2)厚得多[见图4(a)],而磁障几何形状相对于q轴对称。第二层放置在第一层的顶部,而每个单极叠片基本围绕q轴翻转180°,并且这种布置重复直到最后一层。因此,如图4(b)所示,在接合工艺期间,可以在两个连续层之间实现类似于变压器铁芯的重叠图案。重叠区域允许每个单极叠片在顶部和底部与另外两个单极叠片连接,因此,在整个转子叠片上实现了所有单极叠片之间的完全连接,而在未重叠区,每个单极叠片只附加在一个上极和一个下极叠片上,并且在整个转子叠片组中保留有四条剖面线,这降低了接合过程中的机械完整性(见图4(c))。将环氧树脂材料插入各层之间并进行2小时的热压过程后,转子层压完成。为了使转子具有良好的机械完整性和鲁棒性,采用接合技术将转子单极叠片层合在一起。为此,在层间使用环氧胶粘剂材料。每个转子极板包括螺栓孔和导向销,它们在夹紧过程中提供适当的对准导向,如图3和图4所示。两个端板在适当的温度下通过压合技术安装,从而最终完成转子叠层组件。由于同步转速和稳态时转子铁心损耗可忽略不计,因此在所提出的接合方法中,转子温升不是一个问题。为了评价最终转子的机械完整性,在空载试验条件下,装有转子(a)的机械在7500 r/min运行,转子结构不发生任何变形或故障。由于机械约束和安全原因,试验没有以较高的速度进行。
Ⅲ.有限元方法及结果
设计了一台7.5马力的样机,采用两种不同的转子,分别采用CRGO(M5)和CRNGO(冷轧无晶粒取向,M19)。表1总结了设计规范。
表1 样机设计规范
采用集总参数的电流源工作方式进行有限元分析,消除了时间谐波的影响。考虑到转子磁极的对称性,该机采用两个不同的转子以45°的机械间隔运行,减少了仿真时间。转子铁芯的二维磁特性曲线(B-H曲线)根据图2中AK钢的M5规格表征。其他规格在两台机器上保持不变。 结果与下一节中的实验测试结果进行比较。
Ⅳ. 实验测试和结果
图5示出了包括具有CRGO(a)的分段转子和具有各向同性(CRNGO)芯钢(b)的转子的两种不同的转子叠片。 对两台机器进行了转子堵转情况下的交流测试,以确定不同负载下的dq轴电感。
图5(a)分段极和(b)集成极转子叠片
图6和图7分别显示了装有转子(A)和(B)的电机的测量和计算dq轴电感。
图6 转子(a)和(b)q轴电感的测量和计算值
图7 转子(a)和(b)d轴电感的测量和计算值
图8显示了两个转子的转矩角度特性,通过对直流电源的堵转试验,图9显示了它们对应的凸极比与电流的曲线图。
图8 转子(a)和(b)的测量转矩角特性的曲线图
图9 凸极比-电流特性
如图所示,在相同的工作负荷下,当电机装有CRGO钢转子(a)时,d轴的电感较高(见图7),q轴的电感较低(见图6)。这意味着更高的凸极比和更大的输出转矩,分别如图9和图8所示。由于磁通在起动时不能直接测量,因此从测量直交轴电感中获得转子(a)的测量凸极比(见表2,6.8)(见图6和图7)。
表2 测试结果
实验结果不仅包括直接测量,还包括控制变量,如通常在这种实验中所做的那样。 在这种情况下,为了解耦铁磁损耗对磁通量减小的影响并因此对与dq轴电感相关的信号进行解耦,与锁定的转子电源电压相比,供电频率成比例地减小,使得v / f仍然与旋转试验的额定值相同。因此,气隙磁通被认为与频率和铁芯损耗无关,并且与相应的有限元分析结果(见表2,7.6)相当,其中不包括核心损耗。另一方面,用相磁通估计值和用相电流的有限元分析计算的凸极比不同。电流样本数(Delta;Ik)和微分过程的性质是计算凸极比误差的其他原因。总的来说,有限元分析结果显示出稍高的性能( 7.6与6.8 相比),并且与测量值很好地吻合。表二概述了通过试验得到的电机的输出函数。如图所示,在转子铁芯中使用CRGO提高了电机的凸极比(从4.6增加到6.8),并改善最大转矩(从27.3到29.5N·m)。因此,这减少了在相同驱动周期下的堆叠体积和重量,这对于汽车应用是理想的。图10说明了该电机的性能。 包含的转矩和功率-速度特性是为了提供无磁SynRM的特性信息,其中一个是限速范围(1450/850 = 1.70)。因此,在设计中需要进一步的发展,例如使用[15]-[17]中提到的用于牵引应用的永磁体辅助拓扑结构。
图10基于有限元法的该电机转矩/功率-速度特性
Ⅴ. 使用新型转子结构减少转矩脉动
SynRM受到由图11所示的转子各向异性结构引起的高转矩脉动的影响。在[7]和[18]中,阐述了基于正、负全转子几何概念的低转矩脉动方法,以及高性能、高转矩、高电流同步磁阻电机的设计准则。文[19]和[20]介绍了基于转子隔磁磁桥设计的转矩谐波补偿方法。文[21]指出,定子绕组不必采用弦节法,而分布式多层转子可以消除低阶开槽谐波。从减小转矩脉动设计的角度来看,转子和定子槽距角对转矩脉动的影响是已知的。文献表明,对于具有低转矩脉动的转子设计,转子和定子槽距角不能相同,但需要在一个长期复杂的优化过程中加以表征。然而,最终的结果仍然是唯一的,并且不能推广到具有不同几何参数的电机,例如磁极数量、定子和转子槽的数量以及转子内层的数量。本文提出了一种新的数学方法,求解作为最重要的几何参数的转子槽距角的期望值。针对所提出的数学方法的参数性质,该方法可以推广到不同几何参数的同步磁阻电机。制造并检验了一台7.5马力的四极双转子样机,将结果与计算机辅助分析的结果进行比较,以评估所提出的方法。
Ⅵ. 转子和定子槽效应
在同步磁阻电机中,转子受电磁场约束与最小磁阻对齐。这种排列方式的任何改变都会导致开槽区域存储能量的变化,从而导致它们的等效余能发生变化。这些变化取决于转子的位置,是磁转矩的潜在来源。方程(2)和(3)给出了余能及其相应的磁矩的解析表达式如下[22];
Vr是相应区域的体积,delta;是转子角度,Te是磁转矩振幅。
考虑转子和定子开槽引起的转矩脉动的基波,(3)可以表示为 dq电流,磁通量和转子位置的函数如下:
其中lambda;d、lambda;q、id和iq分别为dq轴通量和电流,delta;为转子角度。附加项被添加到表示转矩脉动的转矩方程中对应于开槽效应。然而,该项的平均值保持为零。考虑到dq电感对转子位置的依赖性,式( 4 )中的转矩方程可以重新安排如下[22]:
其中,q为每相每极的槽数。
方程(5)说明转矩脉动由两个分量组成。第一个与卡特系数和循环通量分量(Lcq)振荡引起的平均转矩(idiq)成正比[23],[24]。这两个振荡分别产生dq电感的相当大的变化(Delta;Ld,Delta;Lq),可以通过偏移将其最小化。第二部分介绍了定子和转子开槽的相互作用,引入了Delta;Ldq,并产生了附加的转矩脉动,这是本节所针对的。
Ⅶ. 几何方法标准
转子和定子槽距角(alpha;,beta;)在图11中以四极、36槽定子和四层转子的单极表示示出。
图11 四极同步磁阻电机转子和定子槽距角示意图
原则上,当定子铁芯被磁激励时,产生磁通量波形,转子试图沿最小磁阻的方向对准。这是通过移动转子d轴直到获得电机磁极中磁场的对齐,从而导致转子以与旋转磁场相同的速度旋转来实现的。参照图11,转子叠片的几何形状被设计成使得对于所有磁桥,当给定磁桥( E1 )的一端朝向相应定子槽的开口移动时,磁桥( E2 )的相对端同时远离相应定子槽的开口移动。以这种方式,在电机运行期间,由端部( E2 )产生负转矩脉动,同时由离开相应定子槽开口的磁桥的端部( E1 )产生正转矩脉动。相同的正转矩脉动和负转矩脉动可以彼此抵消,从而减小由转子和定子槽相互作用产生的转矩脉动的总量。平均转矩也最大化。
如图12所示,为了实现这种转子几何形状和减小的转矩脉动特性,需要将两个相邻磁桥端之间的角度间隔,转子槽节距设置为预定值。通过将转子槽节距从角度空间平移到相对于d轴的角度,更容易限定磁桥端部位置。此外,每个转子磁桥端(Rso)被设计为具有与定子槽开口(Sso)相同的宽度(参见图12 )。
图12 单极转子的隔磁磁桥和槽距角
转子磁桥槽开口和角度对转子MMF的影响已在[ 22 ]中详细描述。vagati、Pastorelli、Francheschini和Petrache [18]指出,为了实现低转矩脉动,转子槽的数量(nr)必须基于定子槽的给定数量(ns)来指定,如(6)中所述,其中ns(ns)或nr(nr)必须是偶数。
(6)
转子槽距角对dq MMF振荡的影响已在文献[13]中阐述,并且表示为(7)中beta;1的函数,其是转子的第一磁桥在截止区域处的顶角,并且作为alpha;的控制量。然而,定子槽数的影响被消除
全文共8700字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[16712],资料为PDF文档或Word文档,PDF文档可免费转换为Word


