
英语原文共 9 页
同步磁阻电机驱动的高频信号
注入自适应全阶观测器
- 引言
同步磁阻电机(SYRM)最近重新成为变速驱动器中感应电机的竞争者[1]–[3]。与永磁同步电机(PMSM)相比,SYRM是从定子绕组磁化的,这使得弱磁操作变得简单易行。最近稀土金属的价格上涨也使得SYRM和永磁辅助SYRM相对于PMSM更为有利.
无位置传感器操作通常是首选。在高速时,可以使用基于反电动势(EMF)的方法。因为syrm可以看作是突出的pmm的一个特殊情况,例如,适合突出的pms的基于反电动势的方法,可以对syrm使用[4]和[5]中提出的观察者,但稍作修改。
基于反电动势的方法无法估计位置,低速和静止时。因为SyRM天生就是突出的,精确转子位置估计的方法,即使在静止状态很容易适用。这些方法可以大致分类为:1)信号注入方法[2],[6]–[9];改进的脉宽调制方法[10]、[11];基于无附加信号的定子电流变化[12],[13]。
尽管有些作者赞成使用信号注入方法在所有速度下[14],通常需要避免使用基于反电动势位置的附加噪声和损耗.估计法,结合信号注入法仅适用于最低速度[2]、[15]–[17]。SyRMs通常在额定工作点磁饱和。d轴磁通分量作为相应电流分量的函数具有很强的饱和性。此外,D轴饱和与Q轴饱和耦合。这种交叉饱和在信号注入法得到的位置估计中存在误差。
通常,这种估计误差的补偿要么被忽略,要么通过直接修正输出变量(即位置估计)来实现。本文将自适应全阶观测器与SYRM驱动采用高频信号注入[4],以改善低速运行。该方法进一步改进以考虑电机的交叉饱和,由于信号注入方法提供的信息是通过修正底层全阶观测器的内部状态来使用的,因此在将附加信息引入电机之前,必须对交叉饱和引起的位置误差进行补偿。潜在观察。否则,联合观察者的动态可能会受到损害。
对于任何一个观测器来说,最小的要求是在理想条件下,闭环系统的估计误差动态在每个工作点都是局部稳定的。为了满足这一要求并简化整定过程,以[18]中提出的稳定增益为出发点,对该增益进行了修正,以考虑信号的影响。关于估计误差动力学的一种注记方法
在回顾了第二节中的电机模型和第三节中的转子位置观测器之后,本文的主要贡献在第四节:
1)提出了一种改进的基于信号注入的位置估计方法,降低了交叉饱和引起的稳态估计误差;
2)提出了一种组合观测器的稳定增益修正方法。第五节介绍了实验装置,并利用第六节中的6.7千瓦Syrm驱动器对低速和静止状态下的驱动器性能进行了实验验证
- SYRM模型
A.基本激励模型
这里将使用实空间向量。例如,定子电流矢量为=[ID,IQ]T,ID和IQ是标记向量和矩阵转置的成分,用上标Td轴的电气位置用_m表示。d轴定义为转子最大电感的方向。位置取决于电动角转子速度omega;m,根据
为了简化以下章节中的分析,机器模型将用估计的转子参考框架表示,其D轴与定子在thetasym;circ;m处对齐参考框架。定子电感是
式中thetasym;circ;m minus; thetasym;m为转子位置的估计误差,ld为直轴电感,lq为正交轴电感。坐标变换矩阵用矩阵指数表示,即ethetasym;tilde;mJ =cos thetasym;tilde;mI sin thetasym;tilde;mJ,其中恒等式和正交旋转矩阵为
电压方程为
其中,psi;s是定子磁通矢量,us是定子电压矢量,rs是定子电阻,d omega;circ; m = dthetasym;circ;m/dt是坐标系的角速度。定子电流为
其中值得注意的是电感矩阵l,非线性地依赖于位置估计误差thetasym;tilde;m
B.饱和模型
(2)中的电感ld和lq取决于由于磁饱和而产生的磁通分量(或电流分量)。此项已建模为【19】
- 高频模型
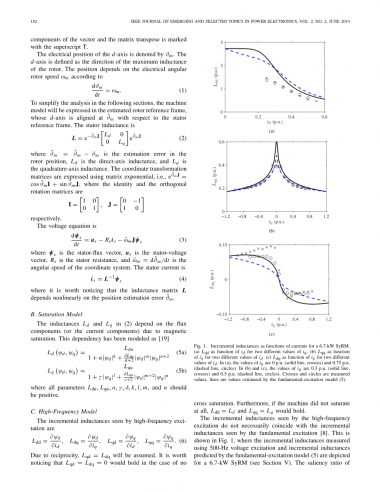
由于相互作用,假设Lqd=ldq。值得注意的是,在没有交叉饱和的情况下,Lqd=ldq=0会保持不变。此外,如果机器完全没有饱和,ldd=ld和lqq=lq将保持不变。高频激励产生的增量电感不一定与基波激励产生的增量电感一致[8]。如图1所示,其中,使用500Hz电压激励测量的增量电感和由基本激励模型(5)预测的增量电感描述了6.7-kw Syrm(见第五节)。本机在额定工作点的突出率约为ld/lq=6.5
在图1(a)中,电感ldd显示为两个不同的iq值的id函数。在图1(b)和(c)中,电感lqq和ldq分别表示为两个不同ID值的iq函数。可以看出,用基本激励模型(线)估计的Ldd和Ldq与测量值(交叉点和圆)有很大的不同,但估计的Lqq与测量值吻合,精度较好。测量值和预测值之间的误差来源于高频信号注入造成的铁损耗。如果注入信号的频率增加,电机将显得不那么突出,最终信号注入的位置
信息将丢失
- 转子位置观测器
无传感器矢量控制SYRM驱动器的框图如图2所示。当驱动器在速度控制模式下运行时,控制系统增加速度控制器,其反馈信号为转子转速估计omega;_m,下面考虑了自适应全阶观测器和误差信号计算。
- 自适应全阶观测器
图3(a)所示的自适应全阶观测器[4]、[20].在可调模型中,定子磁通和定子电流矢量根据
式中, circ;is是估算的定子电流矢量,tilde;is = circ;is minus; is是定子电流的估计误差,K是观测器增益矩阵, Rcirc;s是模型定子电阻.模型电感矩阵是
其中, Lcirc; d 和 Lcirc; q是直轴和正交轴电感模型.分别地,在不失去一般性的情况下,观察者增益矩阵的元素表示为为简化以下方程四个调谐参数分别是k11、k12、k21和k22。估计转子速度使用比例积分(PI)算法
选择增益矢量kp和ki进行估计误差,仅Q轴方向
- 一般稳定增益设计
稳定估计误差动力的每次操作是有精确的模型参数保证的,假设观察者增益矩阵的元素被选为[18]
其中beta;=iq/id和函数Krsquo;11和Krsquo;21是
新的设计参数是b和c,它们应该是正的。为了简化所得到的方程,增益k p和
Ki根据[18]进行缩放。
其中d和e是新的设计参数,取决于转子速度。在这个增益选择中,闭环系统的特征多项式(1)–(4)和(7)–(14)中可以在线性化后分割为两个二阶多项式的积
保证了b,c,d和e所有正值的稳定性。如果模型参数准确.观察者是四阶的,有四个增益。减少设计参数个数d和e可选择为[21]。
产生一个位于S=minus;rho;的双极。剩下的三个设计参数为b、c和rho;,应为正值。总之,在(12)和(14)中选择的增益公式允许直接放置闭环观测器极点(假设线性化系统,精确的模型参数,信号注入法没有修正)
- 高频信号注入
如图2所示,高频电压激励叠加在估计的D轴上的定子电压上方向〔14〕
高频电流响应取决于位置误差
反之
通常,只有高频电流分量位置估计采用垂直于注入信号的方式,然后解调和低通滤波(LPF)。〔21〕,〔22〕
此解调过程仅与图3(b)相对应,只要电流的Q分量用过,使用(18)和(20)产生的准稳态误差信号可以近似为
如果此误差信号被驱动到零,则为非零稳态位置误差
交叉饱和的结果[23]
- 联合观测器
在[4]中提出的组合观测器中,误差信号通过pi算法被驱动到零
该修正omega;与观测者(7)结合,得出
(23)中的收益是
其中alpha;i是PI算法的近似带宽k是误差信号的理想信号注入增益至位置误差thetasym;tilde;m,由
解调过程中考虑了一阶LPF.(20)。滤波器带宽选择为alpha;lp=3alpha;i 符合[4].
从静止到高速运转的平稳过渡通过降低注入电压和随着速度的增加,PI算法的带宽
其中,uc0是注入电压的振幅,alpha;i0是零速度下PI算法的带宽。过渡期函数被选为
在[4]中,增益选择是假定快速通量估计动力学。在Syrms的情况下,通量估计动力学通常不能被忽略。相反,速度跟踪回路(10)必须调整为高带宽(大约是通量估计动力学的10倍)。因此,组合观测器的调谐应重新考虑 SyRMs
IV.提出方案
A.交叉饱和补偿
因为信号注入方法提供的信息更正基础完整顺序的内部状态
观察者根据(24),位置误差交叉饱和的影响(22)最好补偿直接修正错误信号。提出的方法是使用D轴和Q轴电流的组合解调和LPF的组件
其中,Lcirc; dq 和Lcirc; qq是模型增量电感.这种解调过程如图3(b)所示.比例Lcirc; dq/Lcirc; qq可以被视为补偿因子,它可以还包括其他模型和实施不确定性.从图1(c)可以看出,如果iqlt;0, Lcirc; dq/Lcirc; qq gt; 0.如果iqgt;0,Lcirc; dq/Lcirc; qq lt; 0.对于(18)和(29),准稳态误差信号为近似为:
假设模型参数准确,位置误差小,此误差信号减少到
当 thetasym;tilde;m = 0时消失,因此,位置误差导致通过交叉饱和可以理想地降低到零,如果已知比率 Lcirc; dq/Lcirc; qq.此方法与[2]中提出的方法密切相关,这是基于Q轴方向估计的跟踪磁通量变化。但是[2]中的方案要求高振幅载波电压信号及其稳定性分析方法已被省略。
- 观测器增益选择
由于(24)中的校正信号omega;影响了底层全阶观测器的动态特性,观测器增加.由(12)定义的不保证增强系统的稳定性,组合观测器的调谐必须重新考虑.因为信号注入仅应用于最低速度,在(12)和修改后的收益应该是无缝的.不同增益选择对系统稳定性的影响利用线性化方法对组合观测器进行了分析.附录中给出的估计误差动力.数值研究表明,Bgt;0时的增益选择(12)且cgt;0不能保证组合体的稳定性观察者速度非常低.然而,这种不稳定是由于自适应观测器与信号注入校正之间的相互作用可以用修正后的增益来修正.
其中k1和k2是正常数,函数f在(28)中给出。可以看出,这些收益减少到当信号注入时,以更高的速度在(12)中给出的那些方法被禁用。修改后的增益(32)也可以解释为替换观测器参数b和 c/omega;circ; m(13),其中
现在不一定是正面的,可见C1的符号可以是正的也可以是负的,而b1仍为阳性,利用该方法研究了组合观测器的坚固性,附录中给出的线性化估计误差动力学.带正负额定值的静止运行考虑了荷载。实际参数与6.7千瓦Syrm的功率:ld=2.00 p.u.,Lq=0.3 p.u.,且rs=0.042 p.u.调谐参数为:rho;=2 p.u.,uc0=0.1 p.u.,omega;c=2pi;·500 rad/s,omega;= 0.1 P.alpha;i0=0.1 p.u.假设相同的相对不确定度(10%)。
对于所有三个模型参数 Lcirc; d , Lcirc; q 和Rcirc;s.因此,8个不同的最坏情况组合,包括最小值和可以形成模型参数的最大值。例如,最坏情况的组合之一是Lcirc; d = 0.9Ld,Lcirc; q = 1.1Lq,Rcirc;s = 0.9Rs.在每个研究操作下重点分析了系统的局部稳定性错误模型参数的八个最坏情况组合。对模型参数错误的估计误差动力学的稳定性进行了不同参数下的测试。设计参数b和c1。稳定性图如所示.图4:稳定区域为阴影区,不稳定区域为空白。图4(a)和(b)显示了iq=-0.9 p.u.和iq=0.9 p.u.的设计参数空间中的稳定性图。分别的,可以看出稳定区的形状负荷变化,无稳定点.对于c1gt;0,当iq=-0.9 p.u.用于此特定情况时。值得注意的是,组合观测器更好
当应用于永磁同步电机驱动器时,由于稳定性受到控制根据操作点参数beta;,PMSM的参数为[18]
式中,psi;pm为永磁通量。对于PMSMs来说,参数beta;的变化不正比于SYRMs负载变化
v.实验设置及参数
运动无传感器控制系统实现于一个dspace ds1104 ppc/dsp板.A 6.7-kw四极
图4.设计参数空间中10%参数不确定性的稳定性图.(a)iq=minus;0.9 p.u.(b)iq=0.9 p.u.d轴电流为Id=0.45 p.u.,omega;m=0.稳定区为阴影区,不稳定区为空白区.
图5.施加负额定负载扭矩时,斜坡速度反转(0.1 p.u.→0.1 p.u.→0.1 p.u.)的实验结果.D轴电流0.45 p.u.,对交叉饱和的补偿为(a)Lcirc; dq/Lcirc; qq = 0和(b)Lcirc; dq/Lcirc; qq = minus;0.45 · 2/pi; arctan (iq /0.2 p.u.)Syrm由一个受控制的变频器供电.通过DS1104板.Syrm的额定值为:转速3175 r/min,频率105.8 Hz,线对线均方根电压370 V,rms电流15.5 A,扭矩20.1牛米.底座角速度、电压和电流的值定义为2pi;·105.8 rad/s,radic;2/3·370 V和radic;2·15.5 A.伺服电机被用作装载机.转子用增量法测量速度omega;m和位置_m.用于监控的编码器.总惯性矩实验装置的重量为0.015 kgm2(惯性的2.7倍).SYRM转子).测量了定子电流和直流环节电压,以及从电流控制器获得的参考电压
用于观察采样已同步.对于调制,以及开关频率和采样频率为5 kHz.简单电流前馈.死区时间和电源
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


